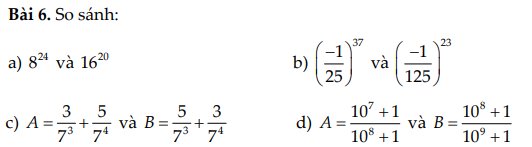
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left(\dfrac{1}{16}\right)^x=\left(\dfrac{1}{2}\right)^{10}\)
=>\(\left(\dfrac{1}{2}\right)^{4x}=\left(\dfrac{1}{2}\right)^{10}\)
=>4x=10
=>x=2,5
b: \(\left(-\dfrac{8}{13}\right)^x=\dfrac{64}{169}\)
=>\(\left(-\dfrac{8}{13}\right)^x=\left(-\dfrac{8}{13}\right)^2\)
=>x=2
c: \(\left(\dfrac{1}{64}\right)^x=\left(-\dfrac{1}{8}\right)^{14}\)
=>\(\left(\dfrac{1}{64}\right)^x=\left(\dfrac{1}{64}\right)^7\)
=>x=7
d: \(\dfrac{27-x}{23}+\dfrac{28-x}{24}=\dfrac{29-x}{25}+\dfrac{30-x}{26}\)
=>\(\left(\dfrac{27-x}{23}-1\right)+\left(\dfrac{28-x}{24}-1\right)=\left(\dfrac{29-x}{25}-1\right)+\left(\dfrac{30-x}{26}-1\right)\)
=>\(\dfrac{4-x}{23}+\dfrac{4-x}{24}=\dfrac{4-x}{25}+\dfrac{4-x}{26}\)
=>\(\left(4-x\right)\left(\dfrac{1}{23}+\dfrac{1}{24}-\dfrac{1}{25}-\dfrac{1}{26}\right)=0\)
=>4-x=0
=>x=4

a: \(64^x:16^x=256\)
=>\(\left(\dfrac{64}{16}\right)^x=256\)
=>\(4^x=256=4^4\)
=>x=4
b: \(-\dfrac{2401}{7^x}=-7\)
=>\(\dfrac{2401}{7^x}=7\)
=>\(7^x=\dfrac{2401}{7}=343=7^3\)
=>x=3
c: \(\dfrac{625}{\left(-5\right)^x}=25\)
=>\(\left(-5\right)^x=\dfrac{625}{25}=25=\left(-5\right)^2\)
=>x=2
a) $64^x:16^x=256$
$\Rightarrow (4^3)^x:(4^2)^x=256$
$\Rightarrow (4^3:4^2)^x=256$
$\Rightarrow 4^x=4^4$
$\Rightarrow x=4$ (tmdk)
b) $\frac{-2401}{7^x}=-7$
$\Rightarrow 7^x=-2401:(-7)$
$\Rightarrow 7^x=343$
$\Rightarrow 7^x=7^3$
$\Rightarrow x=3$ (tmdk)
c) $\frac{625}{(-5)^x}=25$
$\Rightarrow (-5)^x=625:25$
$\Rightarrow (-5)^x=25$
$\Rightarrow (-5)^x=(-5)^2$
$\Rightarrow x=2$ (tmdk)

a: \(\left(\dfrac{2}{3}\right)^6\cdot\left(\dfrac{8}{27}\right)^2=\left(\dfrac{2}{3}\right)^6\cdot\left(\dfrac{2}{3}\right)^6=\left(\dfrac{2}{3}\right)^{12}\)
b: \(\left(\dfrac{3}{5}\right)^2\cdot\left(-\dfrac{9}{25}\right)^2=\left(\dfrac{3}{5}\right)^2\cdot\left(\dfrac{9}{25}\right)^2\)
\(=\left(\dfrac{3}{5}\right)^2\cdot\left(\dfrac{3}{5}\right)^4=\left(\dfrac{3}{5}\right)^6\)
c: \(\left(-\dfrac{5}{2}\right)^3:\left(-\dfrac{8}{125}\right)^3\)
\(=\left(-\dfrac{5}{2}:\dfrac{-8}{125}\right)^3=\left(\dfrac{5}{2}\cdot\dfrac{125}{8}\right)^3=\left(\dfrac{625}{16}\right)^3\)
\(=\left(\dfrac{5}{2}\right)^{12}\)

a: \(\left(\dfrac{2}{3}\right)^5=\dfrac{2^5}{3^5}=\dfrac{32}{243}\)
\(\left(-\dfrac{2}{3}\right)^5=\dfrac{\left(-2\right)^5}{3^5}=\dfrac{-32}{243}\)
\(\left(-1\dfrac{3}{4}\right)^2=\left(-\dfrac{7}{4}\right)^2=\left(\dfrac{7}{4}\right)^2=\dfrac{49}{16}\)
\(\left(-0,1\right)^4=\left(0,1\right)^4=\left(\dfrac{1}{10}\right)^4=\dfrac{1}{10^4}=\dfrac{1}{10000}\)
b: \(\dfrac{90^3}{15^3}=\left(\dfrac{90}{15}\right)^3=6^3=216\)
\(\dfrac{790^4}{79^4}=\left(\dfrac{790}{79}\right)^4=10^4=10000\)
\(\dfrac{3^2}{15^2}=\left(\dfrac{3}{15}\right)^2=\left(\dfrac{1}{5}\right)^2=\dfrac{1}{25}\)
\(\dfrac{\left(-\dfrac{1}{2}\right)^n}{\left(-\dfrac{1}{2}\right)^{n-1}}=\left(-\dfrac{1}{2}\right)^{n-n+1}=\left(-\dfrac{1}{2}\right)^1=-\dfrac{1}{2}\)

\(\dfrac{3}{4}x-6< =0\)
=>\(\dfrac{3}{4}x< =6\)
=>\(x< =6:\dfrac{3}{4}=6\cdot\dfrac{4}{3}=8\)

không hiểu chỗ nào cứ hỏi nha
a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)

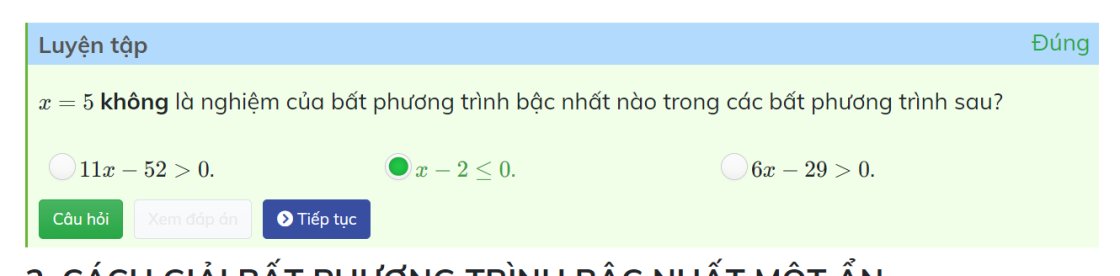
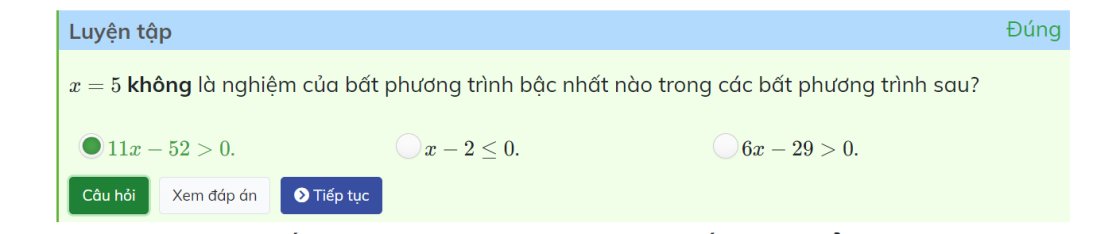
Khi x=5 thì \(11x-52=11\cdot5-52=55-52=3>0\)
=>Đúng
Khi x=5 thì \(6x-29=6\cdot5-29=30-29=1>0\)
=>6x-29>0 đúng
Khi x=5 thì 5-2=3<=0(sai)
=>x-2<=0 là đáp án sai duy nhất, hai cái còn lại đúng
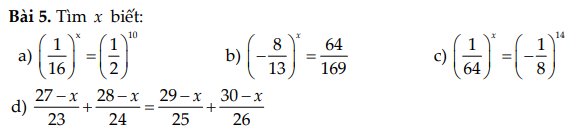
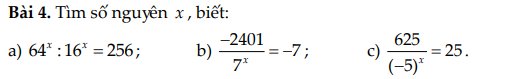
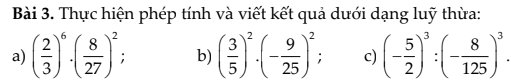
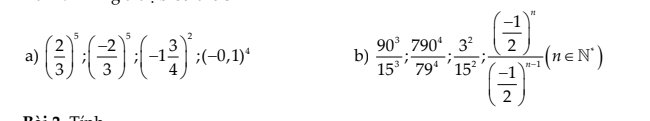

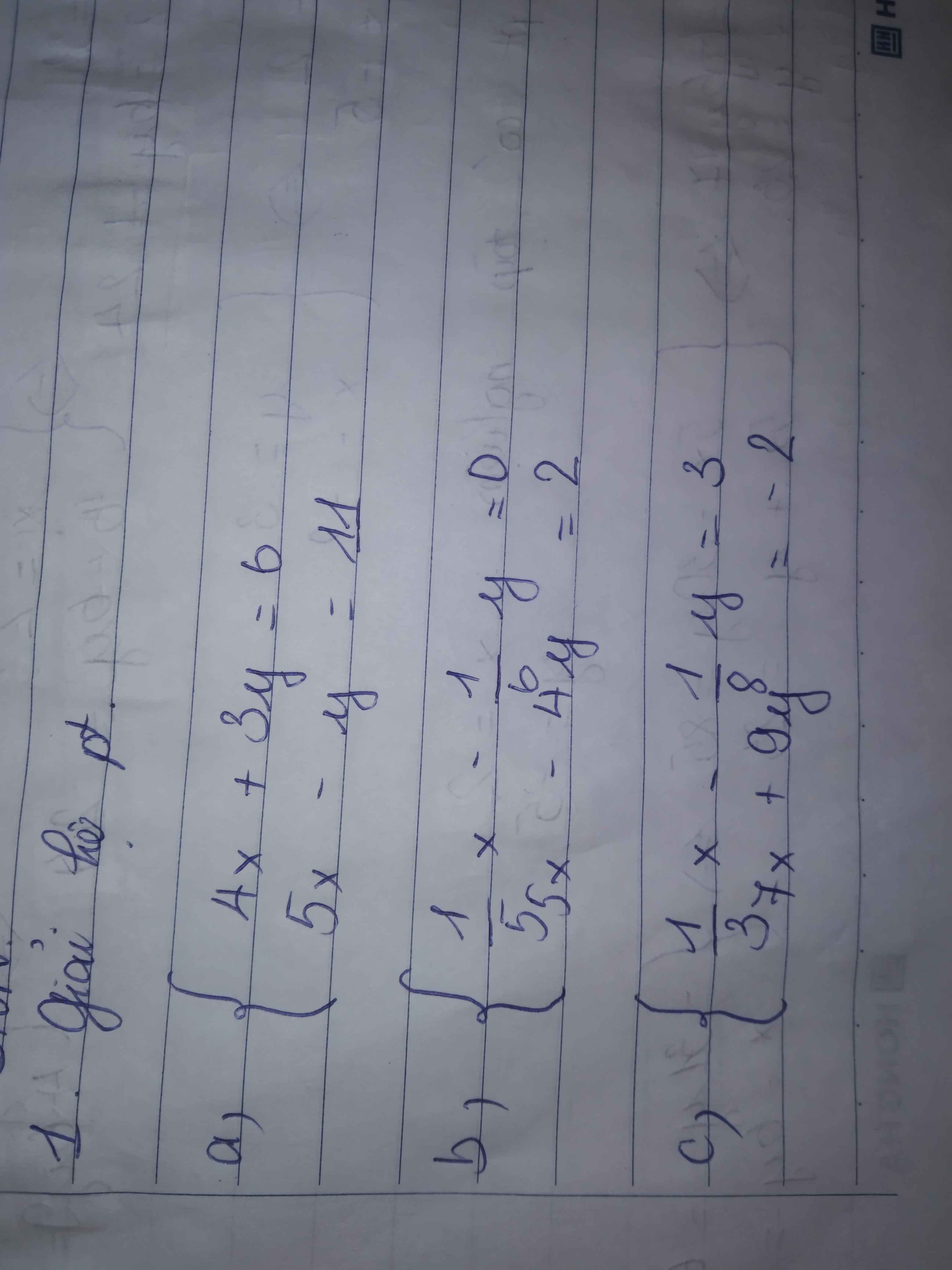
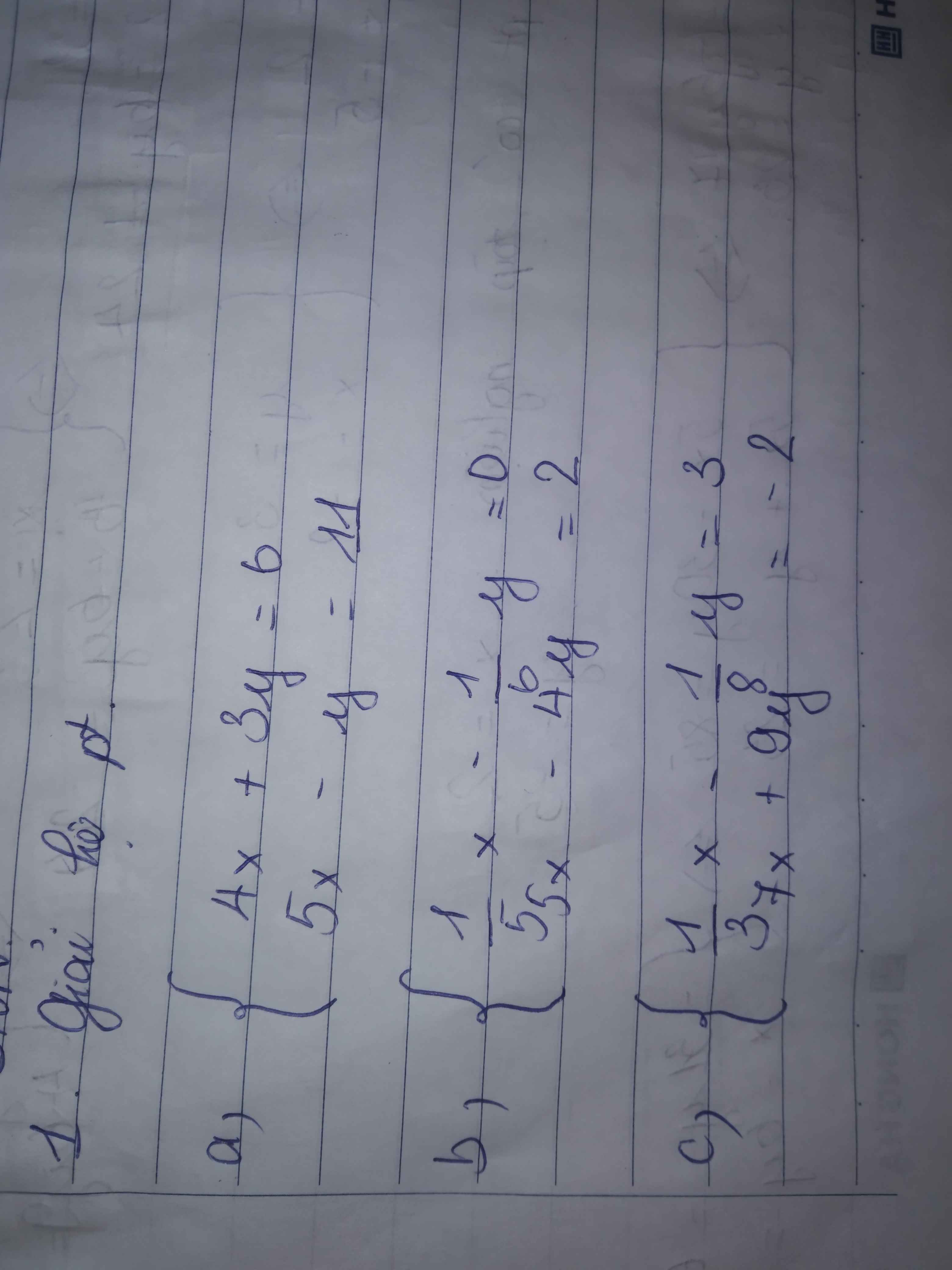
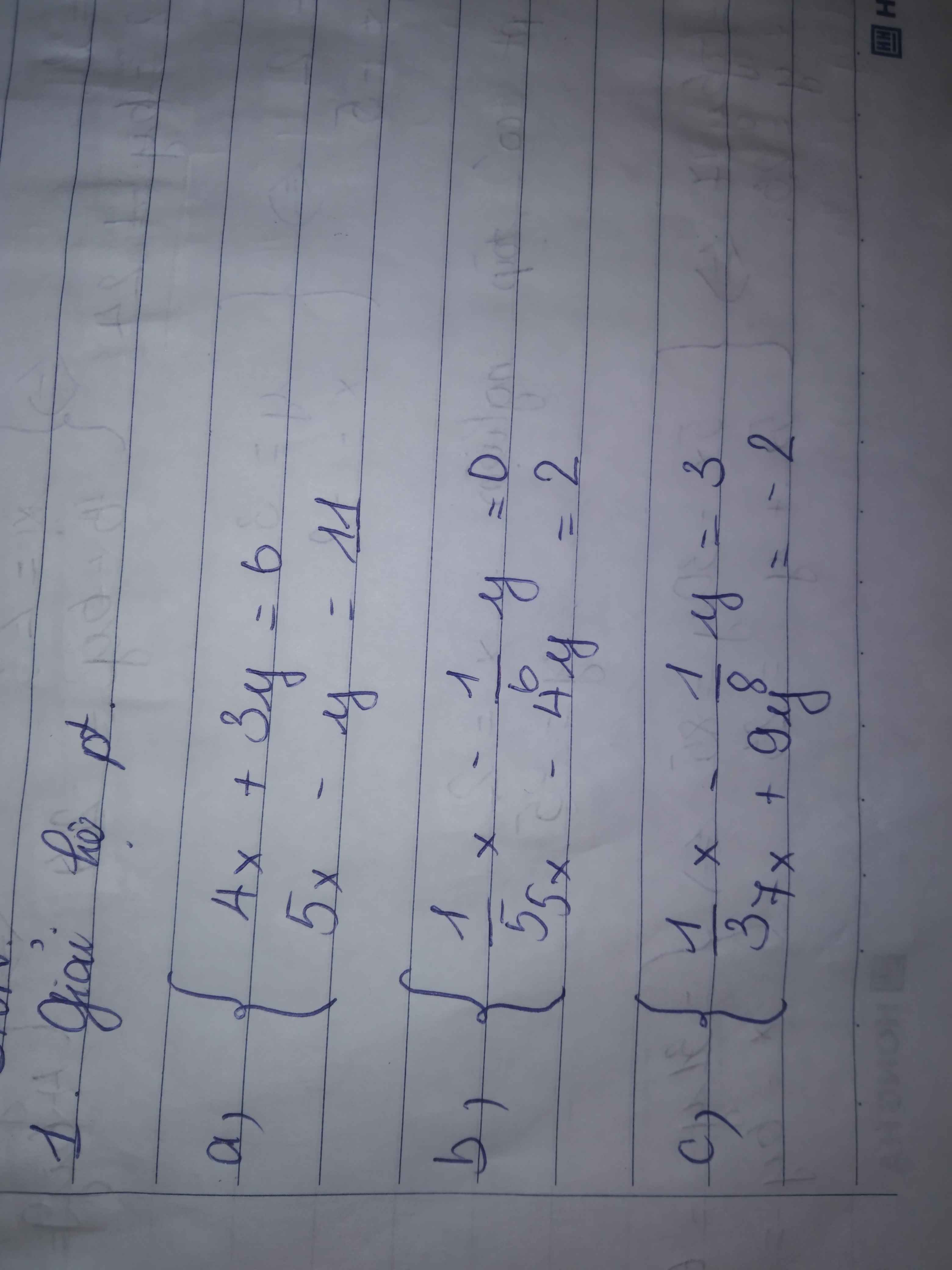
a: \(8^{24}=\left(2^3\right)^{24}=2^{72};16^{20}=\left(2^4\right)^{20}=2^{80}\)
mà 72<80
nên \(8^{24}< 16^{20}\)
b: \(\left(-\dfrac{1}{25}\right)^{37}=-\left(\dfrac{1}{5}\right)^{74}=-\dfrac{1}{5^{74}};\left(-\dfrac{1}{125}\right)^{23}=-\dfrac{1}{\left(5^3\right)^{23}}=-\dfrac{1}{5^{69}}\)
\(5^{74}>5^{69}\)
=>\(\dfrac{1}{5^{74}}< \dfrac{1}{5^{69}}\)
=>\(-\dfrac{1}{5^{74}}>-\dfrac{1}{5^{69}}\)
=>\(\left(-\dfrac{1}{25}\right)^{37}>\left(-\dfrac{1}{125}\right)^{23}\)
c: \(A=\dfrac{3}{7^3}+\dfrac{5}{7^4}=\dfrac{3\cdot7+5}{7^4}=\dfrac{26}{7^4}\)
\(B=\dfrac{5}{7^3}+\dfrac{3}{7^4}=\dfrac{5\cdot7+3}{7^4}=\dfrac{38}{7^4}\)
mà 26<38
nên A<B
d: \(10A=\dfrac{10^8+10}{10^8+1}=1+\dfrac{9}{10^8+1}\)
\(10B=\dfrac{10^9+10}{10^9+1}=1+\dfrac{9}{10^9+1}\)
Ta có: \(10^8+1< 10^9+1\)
=>\(\dfrac{9}{10^8+1}>\dfrac{9}{10^9+1}\)
=>\(\dfrac{9}{10^8+1}+1>\dfrac{9}{10^9+1}+1\)
=>10A>10B
=>A>B