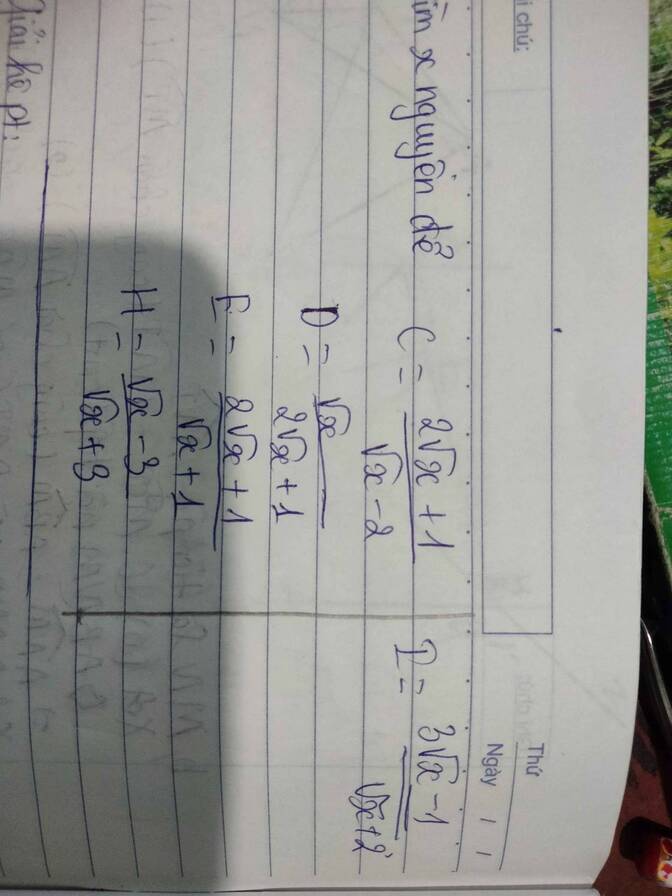 Tìm x để bt nguyê
Tìm x để bt nguyê
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Delta = 4m^2 - 4(2m -1)
= 4m^2 -8m + 4
= (2m)^2 - 2.2m.2 + 2^2
= (2m-2)^2
Delta luôn lớn hơn hoặc bằng 0 với mọi m do đó phương trình luôn có nghiệm với mọi m
b) x1, x2 là nghiệm khi đó ta có x1+x2 = 2m, x1x2 =2m-1
A = x1^2 + x2^2 - 2x1x2
= (x1+x2)^2 - 4x1x2
= (2m)^2 -4(2m-1)
= (2m-2)^2
Ta thấy A nhỏ nhất khi 2m-2 =0 => m= 1

a) \(A=\dfrac{144-\sqrt{144}}{2-\sqrt{144}}=\dfrac{144-12}{2-12}=-13,2\)
b) \(B=\dfrac{x+3}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{2-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(P=AB=\dfrac{x-\sqrt{x}}{2-\sqrt{x}}.\dfrac{2-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
c) \(P< \dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}+1}< \dfrac{1}{3}\) (\(x\ge0,x\ne1,x\ne4\))
\(\Leftrightarrow x+\sqrt{x}+1>3\sqrt{x}\)
\(\Leftrightarrow x-2\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
(đúng do \(x\ne1\))
Bất đẳng thức cuối cùng đúng, mà ta biến đổi tương đương nên bất đẳng thức cần chứng minh đúng.


M A B C D
a/
Ta có A và C cùng nhìn MO dưới 1 góc vuông nên A và C thuộc đường tròn đường kính MO => OAMC là tứ giác nội tiếp)
b/
Ta có
\(\widehat{ADB}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AD\perp MB\)
Xét tg vuông AMO có
\(MA^2=MD.MB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
Mà MA=MC (Hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
=> \(MC^2=MB.MD\)
c/
Khi tg AMO quay xung quang AM thì tạo thành hình chóp có đáy là đường tròn tâm A bán kính OA=R, trung đoạn là MO=2R
\(S_{xq}=\dfrac{1}{2}\Pi R.MO=\Pi.R^2\)

Ta có \(\dfrac{25}{x^2+y^2}+\dfrac{12,5}{xy}=25\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)\)
mà \(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\ge\dfrac{\left(1+1\right)^2}{x^2+y^2+2xy}=\dfrac{4}{\left(x+y\right)^2}=\dfrac{4}{25}\)
=> \(25\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)\ge25.\dfrac{4}{25}=4\)(đpcm)
"=" khi x = y = 2,5
 giúp mình nhâ
giúp mình nhâ 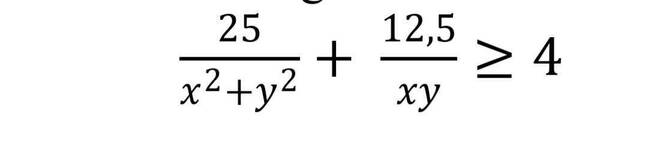 Mong thầy cô chỉ giúp? Cảm ơn thầy co
Mong thầy cô chỉ giúp? Cảm ơn thầy co