Lời giải:

Vì $I$ nằm trên đường trung trực của $BC$ nên $BI=CI$
Vì $I$ nằm trên đường phân giác $\widehat{BAC}$ nên khoảng cách từ $I$ đến $AB$ bằng khoảng cách từ $I$ đến $AC$

$\Rightarrow IH=IK$

Xét tam giác vuông $IHB$ và $IKC$ có:

$IH=IK$ (cmt)

$IB=IC$ (cmt) 

$\Rightarrow \triangle IHB=\triangle IKC$ (ch-gn) 

$\Rightarrow HB=KC$ (đpcm)

Hình vẽ:

Em xem lại số liệu nhé!

Lời giải:
a. Xét tam giác $MHB$ và $MKC$ có:

$\widehat{MHB}=\widehat{MKC}=90^0$

$MB=MC$ (do $M$ là trung điểm $BC$)

$\widehat{MBH}=\widehat{MCK}$ (do $ABC$ cân tại $A$)

$\Rightarrow \triangle MHB=\triangle MKC$ (ch-gn) 

b.

Xét tam giác $MHA$ và $MKA$ có:

$MA$ chung

$\widehat{MHA}=\widehat{MKA}=90^0$

$MH=MK$ (hệ quả từ $\triangle MHB=\triangle MKC$ phần a)

$\Rightarrow \triangle MHA=\triangle MKA$ (ch-cgv) 

Hình vẽ:

       y = k/x (k khác 0)
<=> x = k/y (k khác 0)

Chúc bạn học tốt nhé

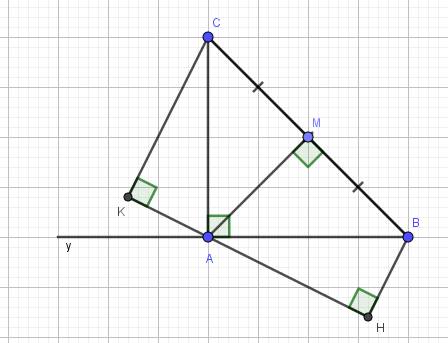
a) Xét hai tam giác vuông:\(\Delta AMB\) và \(\Delta AMC\) có:

\(BM=MC\left(gt\right)\)

AM là cạnh chung

\(\Rightarrow\Delta AMB=\Delta AMC\) (hai cạnh góc vuông)

\(\Rightarrow AB=AC\) (hai cạnh tương ứng)

b) Vẽ tia đối của tia AB là tia Ay

Ta có:

\(AB\perp AC\) (\(\Delta ABC\) vuông tại A)

\(\Rightarrow AC\perp Ay\)

\(\Rightarrow\widehat{yAK}+\widehat{KAC}=90^0\)

Lại có:

\(\widehat{yAK}=\widehat{BAH}\) (đối đỉnh)

\(\Rightarrow\widehat{BAH}+\widehat{KAC}=90^0\)

Mà \(\widehat{ACK}+\widehat{KAC}=90^0\) (\(\Delta ACK\) vuông tại K)

\(\Rightarrow\widehat{BAH}=\widehat{ACK}\)

Do \(\Delta AMB=\Delta AMC\left(cmt\right)\)

\(\Rightarrow AB=AC\) (hai cạnh tương ứng)

Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta CKA\) có:

\(AB=AC\left(cmt\right)\)

\(\widehat{BAH}=\widehat{ACK}\left(cmt\right)\)

\(\Rightarrow\Delta AHB=\Delta CKA\) (cạnh huyền - góc nhọn)