Cho hai số không âm a và b thỏa mãn: căn a + căn b = 1. Tìm giá trị lớn nhất và nhỏ nhất của P = a2 + b2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do (d) đi qua A nên:
\(0.m+n=-1\Rightarrow n=-1\)
\(\Rightarrow y=mx-1\)
Pt hoành độ giao điểm (P) và (d):
\(\dfrac{1}{2}x^2=mx-1\Leftrightarrow x^2-2mx+2=0\) (1)
(d) tiếp xúc (P) khi và chỉ khi (1) có nghiệm kép
\(\Rightarrow\Delta'=m^2-2=0\Rightarrow m=\pm\sqrt{2}\)
- Với \(m=\sqrt{2}\Rightarrow x=-\dfrac{b}{2a}=\sqrt{2}\Rightarrow y=\dfrac{1}{2}x^2=1\)
Tọa độ tiếp điểm là \(\left(\sqrt{2};1\right)\)
- Với \(m=-\sqrt{2}\Rightarrow x=-\dfrac{b}{2a}=-\sqrt{2}\Rightarrow y=1\)
Tọa độ tiếp điểm là \(\left(-\sqrt{2};1\right)\)

a) Ta có tam giác nhọn ABC nội tiếp đường tròn (O), BE là đường cao của tam giác ABC và cắt AC tại H, CF là đường cao của tam giác ABC và cắt AB tại F.
Chứng minh tam giác AEHF nội tiếp:
Gọi I là giao điểm của BF và CE. Ta có:
- Do ABC nội tiếp đường tròn (O), ta có ∠BAC = ∠BIC = 90°.
- Ta có BE ⊥ AC và CF ⊥ AB, nên BE // CF.
- Do đó, ta có ∠BEC = ∠BCF.
- Vậy tam giác BEC và BCF đồng dạng.
- Từ đó, ta có ∠BED = ∠BCF = ∠BAC.
- Vậy tam giác ABE và ABC đồng dạng.
- Từ đó, ta có ∠AEH = ∠ABC = ∠AFH.
- Vậy ta kết luận được tam giác AEHF nội tiếp.
b) Chứng minh AH ⊥ BC:
Vì tam giác AEHF nội tiếp, nên ta có ∠AEH = ∠AFH.
- Như đã chứng minh ở phần a), ta có ∠AEH = ∠ABC.
- Và ∠AFH = ∠ACB.
- Vậy ta có ∠ABC = ∠ACB.
- Vậy ta kết luận được AH ⊥ BC.
c) Chứng minh AO là đường trung trực của PG:
Gọi O là tâm của đường tròn nội tiếp tam giác ABC.
- Gọi M là trung điểm của đoạn thẳng EF.
- Ta có ∠AEM = ∠AFM = 90° (do EM ⊥ BE, FM ⊥ CF).
- Và ta có ∠AEF = ∠AFM và ∠AFE = ∠AEM.
- Vậy tam giác AEF đồng dạng với tam giác AMF.
- Từ đó, ta có AO là đường trung trực của PG.

a) Ta có \(M\left(1,m\right)\) và \(N\left(-3,n\right)\).
Vì \(M,N\in\left(P\right):y=\dfrac{1}{2}x^2\) nên ta suy ra \(m=\dfrac{1}{2};n=\dfrac{9}{2}\)
Gọi đường thẳng cần tìm là \(d:y=ax+b\). Vì \(d\) đi qua M và N nên ta có hệ pt sau:
\(\left\{{}\begin{matrix}\dfrac{1}{2}=a+b\\\dfrac{9}{2}=-3a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=\dfrac{3}{2}\end{matrix}\right.\).
Vậy ptđt cần tìm là \(d:y=-x+\dfrac{3}{2}\)
b) Mình chưa hiểu đề bài lắm. Thế nào là "cắt parabol tại 2 điểm đạt GTNN"?


a) Nhận thấy \(\widehat{OBK}=\widehat{OAK}=90^o\) \(\Rightarrow\) Tứ giác OAKB nội tiếp đường tròn (OK).
Mặt khác \(\widehat{OHK}=90^o\) nên \(H\in\left(OK\right)\)
\(\Rightarrow\) 5 điểm A, B, O, K, H cùng thuộc đường tròn (OK).
b) Từ câu a) \(\Rightarrow\) Tứ giác OAHB nội tiếp
\(\Rightarrow\widehat{IHB}=\widehat{IAO}\)
Từ đó dễ dàng chứng minh \(\Delta IHB~\Delta IAO\left(g.g\right)\)
\(\Rightarrow\dfrac{IH}{IA}=\dfrac{IB}{IO}\) \(\Rightarrow IA.IB=IH.IO\) (đpcm)
c) Gọi T là giao điểm của OK và AB.
Tính chất của 2 tiếp tuyến cắt nhau \(\Rightarrow OK\perp AB\) tại T
Tam giác OAK vuông tại A có đường cao AT nên \(OT.OK=OA^2\) (hệ thức lượng trong tam giác vuông)
Xét tam giác OTI và OHK, ta có:
\(\widehat{HOK}\) chung , \(\widehat{OTI}=\widehat{OHK}=90^o\)
\(\Rightarrow\Delta OTI~\Delta OHK\left(g.g\right)\)
\(\Rightarrow\dfrac{OT}{OH}=\dfrac{OI}{OK}\)
\(\Rightarrow OT.OK=OH.OI\)
Mà \(OT.OK=OA^2\) (cmt) \(\Rightarrow OH.OI=OA^2\)
\(\Rightarrow OI=\dfrac{OA^2}{OH}\) là một hằng số
\(\Rightarrow\) I thuộc đường tròn \(\left(O;\dfrac{OA^2}{OH}\right)\) cố định
Hơn nữa I nằm trên đường thẳng OH cố định nên I cố định
\(\Rightarrow\) AB đi qua I cố định.

Điểm F ở câu a) với điểm N ở câu b) là những điểm gì thế bạn? Mình thấy trong đề không có định nghĩa các điểm này.

Với \(0< x< \sqrt{3}\) ta có đánh giá sau:
\(\dfrac{1}{2-x}\ge\dfrac{x^2+1}{2}\)
Thực vậy, do \(x< \sqrt{3}\Rightarrow2-x>0\), BĐT tương đương:
\(2\ge\left(2-x\right)\left(x^2+1\right)\)
\(\Leftrightarrow x^3-2x^2+x\ge0\)
\(\Leftrightarrow x\left(x-1\right)^2\ge0\) (luôn đúng với \(x>0\))
Áp dụng cho bài toán:
\(\dfrac{1}{2-a}+\dfrac{1}{2-b}+\dfrac{1}{2-c}\ge\dfrac{a^2+1}{2}+\dfrac{b^2+1}{2}+\dfrac{c^2+1}{2}=\dfrac{a^2+b^2+c^2+3}{2}=3\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)

Trước khi xem lời giải của mình thì bạn chú ý là trong đó có sử dụng những kí hiệu, thuật ngữ và tính chất khá khó hiểu với học sinh cấp II (thậm chí một vài bạn cấp III cũng chưa chắc đã hiểu thấu). Vì vậy nếu có gì khúc mắc trong lời giải thì bạn cứ nhắn tin riêng cho mình nhé.
Trước hết ta đến với các định nghĩa sau:
Định nghĩa 1: Với điểm X nằm ngoài đường tròn (I), kí hiệu \(d_X\) là đường thẳng nối 2 tiếp điểm của 2 tiếp tuyến qua X ứng với (I).
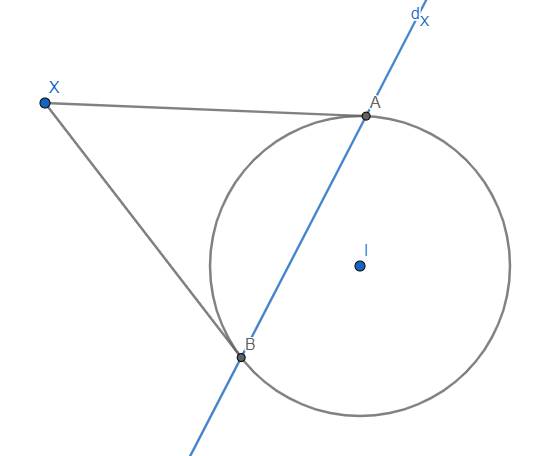
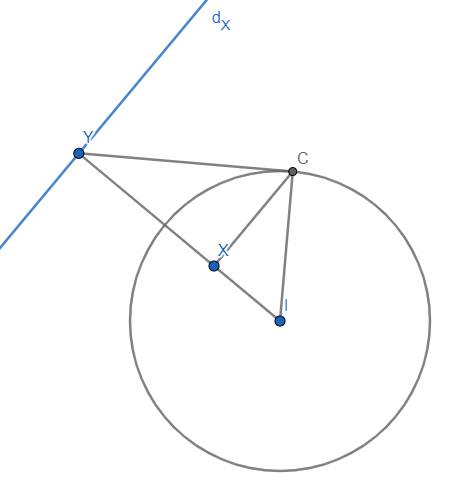
Định nghĩa 2: Còn với điểm (I) nằm trong đường tròn, nếu lấy điểm Y trên tia IX mà \(IY.IX=R^2\) thì dX lại là đường thẳng qua Y và vuông góc với IX.
Định nghĩa 3: Bốn điểm A, B, C, D theo thứ tự nằm trên 1 đường thẳng mà thỏa mãn \(\dfrac{AB}{AD}=\dfrac{CB}{CD}\) thì ta kí hiệu \(\left(BDCA\right)=-1\) và nếu lấy một điểm O bất kì nằm ngoài đường thẳng đó thì ta kí hiệu \(O\left(BDCA\right)=\left(OB,OD,OC,OA\right)=-1\)
Sau đây là một số tính chất:
Tính chất 1: \(d_X\perp IX\), hiển nhiên.
Tính chất 2: \(Y\in d_X\Leftrightarrow X\in d_Y\) , cũng quá hiển nhiên.
Tính chất 3: Từ một điểm X nằm ngoài I, vẽ cát tuyến XUV với U, V thuộc (I). Khi đó một điểm Y bất kì thuộc cát tuyến này mà thỏa mãn \(\left(UVYX\right)=-1\) \(\Leftrightarrow Y\in d_X\).
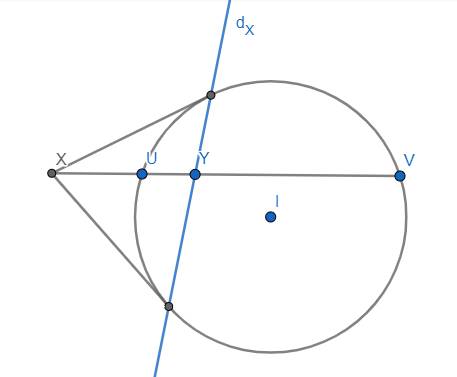
Tính chất 4: Cho 4 điểm A, B, C, D theo thứ tự nằm trên đường thẳng d thỏa mãn \(\left(BDCA\right)=-1\) và 1 điểm O nằm ngoài d. Khi đó nếu vẽ 1 đường thẳng d' khác d cắt OA, OB, OC, OD lần lượt tại A', B', C', D' thì \(\left(B'D'C'A'\right)=-1\)
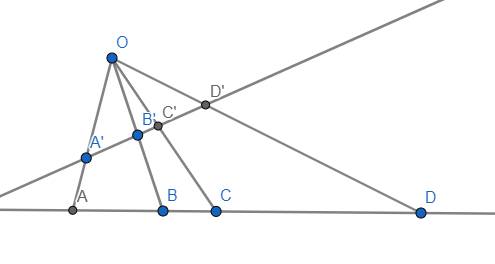
Tính chất 5: Cho 4 điểm A, B, C, D nằm trên d và một điểm O nằm ngoài d. Khi đó kẻ một đường thẳng song song với một đường bất kì trong số OA, OB, OC, OD và cắt 3 đường còn lại tại M, N, P (N nằm giữa M và P). Khi đó M là trung điểm của NP \(\Leftrightarrow\left(BDCA\right)=-1\)
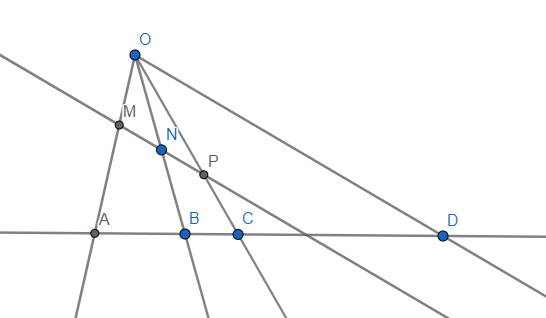
Quay trở lại bài toán chính.
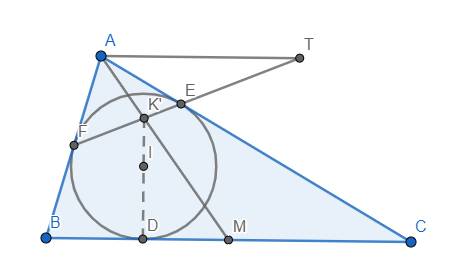
Gọi M là trung điểm BC, K' là giao điểm của AM và EF. Qua A kẻ đường thẳng song song với BC cắt EF tại T.
Ta sẽ chứng minh \(K'\equiv K\) hay D, E, K' thẳng hàng.
Thật vậy, vì AT//BC và M là trung điểm BC nên theo tính chất 5\(\left(AB,AC,AM,AT\right)=-1\). Áp dụng tính chất 4, ta được \(\left(EFK'T\right)=-1\), điều này có nghĩa là \(T\in d_{K'}\) do tính chất 3.
Hơn nữa, \(K'\in EF\equiv d_A\) nên \(A\in d_{K'}\) (tính chất 2). Do đó \(AT\equiv d_{K'}\) dẫn đến \(IK'\perp AT\) (tính chất 1).
Do AT//BC nên \(IK'\perp BC\). Mà \(ID\perp BC\) nên D, I, K' thẳng hàng hay \(K'\equiv K\). Ta có đpcm.
\(P=\left(a^2+\dfrac{1}{16}+\dfrac{1}{16}+\dfrac{1}{16}\right)+\left(b^2+\dfrac{1}{16}+\dfrac{1}{16}+\dfrac{1}{16}\right)-\dfrac{3}{8}\)
\(P\ge4\sqrt[4]{\dfrac{a^2}{16^3}}+4\sqrt[4]{\dfrac{b^2}{16^3}}-\dfrac{3}{8}=\dfrac{1}{2}\left(\sqrt{a}+\sqrt{b}\right)-\dfrac{3}{8}=\dfrac{1}{8}\)
\(P_{min}=\dfrac{1}{8}\) khi \(a=b=\dfrac{1}{4}\)
Do \(\left\{{}\begin{matrix}a;b\ge0\\\sqrt{a}+\sqrt{b}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}0\le a\le1\\0\le b\le1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{a}\ge a^2\\\sqrt{b}\ge b^2\end{matrix}\right.\)
\(\Rightarrow a^2+b^2\le\sqrt{a}+\sqrt{b}=1\)
\(P_{max}=1\) khi \(\left(a;b\right)=\left(1;0\right);\left(0;1\right)\)