Một vườn hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu tăng thêm mỗi cạnh lên 5 m thì diện tích khu vườn tăng thêm 385 m2. Tìm kích thước ban đầu của hình chữ nhật ấy?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
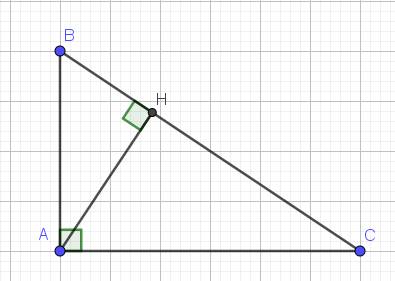
a. Xét tam giác $ABC$ và $HBA$ có:
$\widehat{B}$ chung
$\widehat{BAC}=\widehat{BHA}=90^0$
$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)
Ta có:
$AB.AC=AH.BC$ (cùng bằng 2 lần diện tích tam giác $ABC$)
b.
Xét tam giác $BHA$ và $AHC$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{HBA}=\widehat{HAC}$ (cùng phụ góc $\widehat{BAH}$)
$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)
$\Rightarrow \frac{BH}{HA}=\frac{AH}{HC}$
$\Rightarrow AH^2=BH.CH$.

a, Xét \(\Delta ADC\) và \(\Delta BKC\), ta có:
\(\widehat{D}\) = \(\widehat{K}\) = 90 độ
\(\widehat{C}\) chung
\(\Rightarrow\)\(\Delta ADC\) đồng dạng \(\Delta BKC\)
b, thiếu dữ kiện

Lời giải:
Gọi $H$ là chân đường cao kẻ từ $A$ xuống $BC$. Vì $ABC$ cân tại $A$ nên $H$ là trung điểm của $BC$
$\Rightarrow HB=BC:2=3$ (cm)
Áp dụng định lý Pitago: $AH=\sqrt{AB^2-HB^2}=\sqrt{5^2-3^2}=4$ (cm)
Diện tích đáy: $S_{ABC}=\frac{AH.BC}{2}=\frac{4.6}{2}=12$ (cm2)
Thể tích: $AA'.S_{ABC}=9.12=108$ (cm3)
Diện tích xung quanh: $P_{ABC}.AA'=(AB+BC+AC).AA'=(5+5+6).9=144$ (cm2)
Diện tích toàn phần: $144+2\times 12=168$ (cm2)

Lời giải:
a.
$A=\frac{3x+15}{(x-3)(x+3)}+\frac{x-3}{(x+3)(x-3)}-\frac{2(x+3)}{(x-3)(x+3)}$
$=\frac{3x+15+(x-3)-2(x+3)}{(x+3)(x-3)}=\frac{2x+6}{(x-3)(x+3)}$
$=\frac{2(x+3)}{(x-3)(x+3)}=\frac{2}{x-3}$
b.
Để $A=\frac{1}{2}$
$\Leftrightarrow \frac{2}{x-3}=\frac{1}{2}$
$\Leftrightarrow x-3=4$
$\Leftrightarrow x=7$ (tm)

Trong 1 giờ hai người cùng làm được: 1 : 10 = \(\dfrac{1}{10}\) ( công việc)
Theo bài ra ta có số ngày hai người làm chung công việc là:
6 + 3 = 9 ( ngày)
Số phần công việc hai người cùng làm trong 9 ngày là:
\(\dfrac{1}{10}\) \(\times\) 9 = \(\dfrac{9}{10}\)
Số phần công việc người thứ hai phải làm một mình trong 3 ngày là:
1 - \(\dfrac{9}{10}\) = \(\dfrac{1}{10}\) ( công việc)
Trong 1 ngày người thứ hai làm một mình được:
\(\dfrac{1}{10}\): 3 = \(\dfrac{1}{30}\) ( công việc)
Nếu làm một mình thì người thứ hai làm xong công việc sau:
1 : \(\dfrac{1}{30}\) = 30 ( ngày)
Trong 1 giờ người thứ nhất làm một mình được:
\(\dfrac{1}{10}\) - \(\dfrac{1}{30}\) = \(\dfrac{1}{15}\) ( công việc)
Người thứ nhất nếu làm một mình sẽ xong công việc sau:
1: \(\dfrac{1}{15}\) = 15 ( ngày)
Kết luận: Người thứ nhất hoàn thành công việc nếu làm một mình sau 15 ngày
Người thứ hai làm một mình sẽ xong công viêc sau 30 ngày


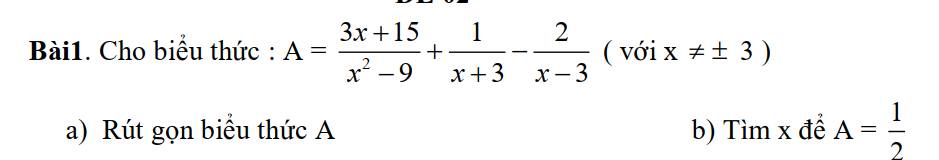
Lời giải:
Gọi chiều rộng khu vườn là $a$ (m) thì chiều dài là $3a$ (m)
Diện tích ban đầu: $a.3a=3a^2$ (m2)
Diện tích sau khi đổi: $(a+5)(3a+5)$ (m2)
Có: $(a+5)(3a+5)-3a^2=385$
$\Leftrightarrow 20a+25=385$
$\Rightarrow a=18$ (m)
Vậy chiều rộng ban đầu là 18 m và chiều dài là $18.3=54$ m