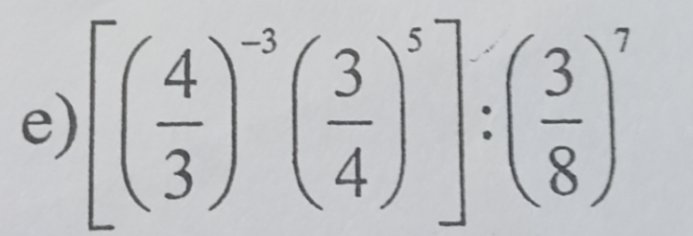
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hiệu của hai số khi tăng số lớn thêm 3 đơn vị và giảm số bé đi 2 đơn vị là:
35+3-(-2)=38+2=40
Số lớn khi đó là 40:4x5=50
Số lớn là 50-3=47
Số bé là 47-35=12

a: \(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\9x+3y=27\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+3y-x-3y=27-11\\x+3y=11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x=16\\3y=11-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{11-x}{3}=\dfrac{11-2}{3}=\dfrac{9}{3}=3\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+10y-3x=-1\\2x+4-3x+15y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y=-1\\-x+15y=-16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\-2x+30y=-32\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y-2x+30y=-1+\left(-32\right)\\x-15y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}40y=-33\\x=15y+16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=15\cdot\dfrac{-33}{40}+16=\dfrac{29}{8}\end{matrix}\right.\)
a)
\(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+9y=33\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}8y=24\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\3x+3=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3\\x=\dfrac{6}{3}=2\end{matrix}\right.\)
b)
\(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x+10y=3x-1\\2x+4=3x-15y-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\2x-30y=32\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}40y=-33\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x+\dfrac{99}{8}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=16-\dfrac{99}{8}=\dfrac{29}{8}\end{matrix}\right.\)

Bài 4.Trong các phép so sánh sau, phép so sánh nào sai?
A. 71,56 < 71,65 B. 71,506 > 71,056
C. 716,05 > 716,005 D. 716,50 < 716,500
Vì 716,50 = 716,5 ; 716, 500 = 716,5 nên 716,50 < 716,500 là sai.

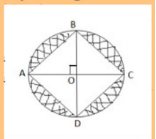
Chu vi hình vuông ABCD là 56cm
=>4xAB=56cm
=>AB=56/4=14(cm)
\(AC=\sqrt{14^2+14^2}=14\sqrt{2}\left(cm\right)\)
=>\(OA=OC=\dfrac{14\sqrt{2}}{2}=7\sqrt{2}\left(cm\right)\)
Diện tích hình tròn tâm O là:
\(S_{\left(O\right)}=OA\times OA\times3,14=307,72\left(cm^2\right)\)
Diện tích hình vuông ABCD là:
\(S_{ABCD}=14\times14=196\left(cm^2\right)\)
Diện tích phần gạch chéo là:
307,72-196=111,72(cm2)

\(\dfrac{x+100}{4}+\dfrac{x+99}{5}=\dfrac{x+98}{6}+\dfrac{x+97}{7}\)
=>\(\left(\dfrac{x+100}{4}+1\right)+\left(\dfrac{x+99}{5}+1\right)=\left(\dfrac{x+98}{6}+1\right)+\left(\dfrac{x+97}{7}+1\right)\)
=>\(\dfrac{x+104}{4}+\dfrac{x+104}{5}=\dfrac{x+104}{6}+\dfrac{x+104}{7}\)
=>\(\left(x+104\right)\left(\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}-\dfrac{1}{7}\right)=0\)
=>x+104=0
=>x=-104
\(\dfrac{x+100}{4}+\dfrac{x+99}{5}=\dfrac{x+98}{6}+\dfrac{x+97}{7}\\ \dfrac{x+100}{4}+\dfrac{x+99}{5}-\dfrac{x+98}{6}-\dfrac{x+97}{7}=0\\ \left(\dfrac{x+100}{4}+1\right)+\left(\dfrac{x+99}{5}+1\right)-\left(\dfrac{x+98}{6}+1\right)-\left(\dfrac{x+97}{7}+1\right)=0\\ \dfrac{x+104}{4}+\dfrac{x+104}{5}-\dfrac{x+104}{6}-\dfrac{x+104}{7}=0\\ \left(x+104\right)\cdot\left(\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}-\dfrac{1}{7}\right)=0\)
Vì \(\left(\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}-\dfrac{1}{7}\right)\ne0\) nên:
\(x+104=0\\ x=-104\)
Vậy \(x=-104\)


a: Các cặp góc đối đỉnh là: \(\widehat{xOt};\widehat{yOz}\) và \(\widehat{xOz};\widehat{yOt}\)
b: Các cặp góc kề bù là:
\(\widehat{xOt};\widehat{xOz}\)
\(\widehat{xOt};\widehat{tOy}\)
\(\widehat{zOy};\widehat{zOx}\)
\(\widehat{zOy};\widehat{tOy}\)
c: \(\widehat{xOt}+\widehat{xOz}=180^0\)(hai góc kề bù)
=>\(\widehat{xOz}+45^0=180^0\)
=>\(\widehat{xOz}=135^0\)
Ta có: \(\widehat{xOt}=\widehat{yOz}\)(hai góc đối đỉnh)
mà \(\widehat{xOt}=45^0\)
nên \(\widehat{yOz}=45^0\)
Ta có: \(\widehat{xOz}=\widehat{yOt}\)(hai góc đối đỉnh)
mà \(\widehat{xOz}=135^0\)
nên \(\widehat{yOt}=135^0\)

Số dư là số lớn nhất có thể
=>Số dư=số chia -1
Vì số bị chia là 143, thương là 11, số dư là số lớn nhất có thể
=>12 lần số chia là 143+1=144
Số chia là 144:12=12
\(\left[\left(\dfrac{4}{3}\right)^{-3}\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\\ =\left[\left(\dfrac{3}{4}\right)^3\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\\ =\left(\dfrac{3}{4}\right)^{3+5}:\dfrac{3^7}{8^7}\\ =\left(\dfrac{3}{4}\right)^8\cdot\dfrac{8^7}{3^7}\\ =\dfrac{3^8}{4^8}\cdot\dfrac{8^7}{3^7}\\ =\dfrac{3^8}{2^{16}}\cdot\dfrac{2^{21}}{3^7}=3\cdot2^5=3\cdot32=96\)
\(\left[\left(\dfrac{4}{3}\right)^{-3}\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\)
\(=\left[\left(\dfrac{3}{4}\right)^3\cdot\left(\dfrac{3}{4}\right)^5\right]:\dfrac{3^7}{8^7}\)
\(=\left(\dfrac{3}{4}\right)^8\cdot\dfrac{8^7}{3^7}=\dfrac{3^8}{4^8}\cdot\dfrac{8^7}{3^7}=\dfrac{3\cdot2^{21}}{2^{16}}=3\cdot2^5=3\cdot32=96\)