Giải giúp vơi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Có AH là đường cao của Δ ABC (gt)
=> AH ⊥ BC tại H
=> Δ ABH vuông tại H
=> \(AB^2=AH^2+BH^2\) (py-ta-go)
=> BH² = AB² – AH² = 36 – (4,8)² = 12,96
=> BH = 3,6 cm
áp dụng hệ thức lượng trong Δ ABC ta có
AB² = BH.BC
=> \(BC=\dfrac{AB^2}{BH}=\dfrac{36}{3,6}=10cm\)
khi đó diện tích \(\Delta ABC=\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.4,8.10=24cm^2\)
Cách 2:
Áp dụng hệ thức lượng trong Δ ABC ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay \(AH^2=\dfrac{AB^2.AC^2}{AB^2+AC^2}\)
=>\(\left(4,8\right)^2=\dfrac{36.AC^2}{36+AC^2}\)
=> AC =8 cm
Khi đó diện tích\(\Delta ABC=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.6.8=24cm^2\)

a) Xét (O) có \(\widehat{DBC}\) và \(\widehat{DAB}\) lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{BC}\) nên ta có \(\widehat{DBC}=\widehat{DAB}\). Từ đó, ta dễ dàng chứng minh \(\Delta DBC~\Delta DAB\left(g.g\right)\) \(\Rightarrow\dfrac{DC}{DB}=\dfrac{DB}{DA}\) \(\Rightarrow BD^2=AD.CD\) (đpcm)
b) Gọi I là giao điểm của BD và CE.
Xét (O) có 2 tiếp tuyến tại B và C cắt nhau tại I nên \(IB=IC\), dẫn đến tam giác IBC cân tại I, từ đó \(\widehat{IBC}=\widehat{ICB}\) (1)
Tam giác ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\) \(\Rightarrow180^o-\widehat{ABC}=180^o-\widehat{ACB}\) \(\Rightarrow\widehat{EBC}=\widehat{DCB}\) (2)
Từ (1) và (2), ta có \(\widehat{EBC}-\widehat{IBC}=\widehat{DCB}-\widehat{ICB}\) \(\Rightarrow\widehat{DBE}=\widehat{DCE}\)
Từ đó dễ dàng chứng minh tứ giác BCDE nội tiếp.
c) Tứ giác BCDE nội tiếp nên \(\widehat{EBC}+\widehat{CDE}=180^o\)
Mà \(\widehat{EBC}=\widehat{DCB}\) nên \(\widehat{DCB}+\widehat{CDE}=180^o\) \(\Rightarrow BC//DE\) (2 góc trong cùng phía bù nhau)

\(a,b,c\ge1\) chứ nhỉ?
\(a^5+b^5+c^5\ge a+b+c\)
\(\Leftrightarrow a^5+b^5+c^5-a-b-c\ge0\)
\(\Leftrightarrow a\left(a^4-1\right)+b\left(b^4-1\right)+c\left(c^4-1\right)\ge0\)
- Điều này đúng do \(a,b,c\ge1\)
- Vậy BĐT đã được c/m.

Với \(a > 0,a \ne 1\) có:
\(\dfrac{(\dfrac{\sqrt{a}+2}{a+2\sqrt{a}+1}-\dfrac{\sqrt{a}-2}{a-1})}{\dfrac{\sqrt{a}}{\sqrt{a}+1}}\)
\(=(\dfrac{\sqrt{a}+2}{a+2\sqrt{a}+1}-\dfrac{\sqrt{a}-2}{a-1}):\dfrac{\sqrt{a}}{\sqrt{a}+1}\)
\(=\dfrac{(\sqrt{a}+2)(\sqrt{a}-1)-(\sqrt{a}-2)(\sqrt{a}+1)}{(\sqrt{a}-1)(\sqrt{a}+1)^2}.\dfrac{\sqrt{a}+1}{\sqrt{a}}\)
\(=\dfrac{a-\sqrt{a}+2\sqrt{a}-2-a-\sqrt{a}+2\sqrt{a}+2}{(\sqrt{a}-1)(\sqrt{a}+1)}.\dfrac{1}{\sqrt{a}}\)
\(=\dfrac{2\sqrt{a}}{a-1}.\dfrac{1}{\sqrt{a}}=\dfrac{2}{a-1}\)

Ta có \(\sqrt{16-6\sqrt{7}}=\sqrt{9-2.3.\sqrt{7}+7}\) \(=\sqrt{\left(3-\sqrt{7}\right)^2}=3-\sqrt{7}\)
Và \(\sqrt{29-4\sqrt{7}}=\sqrt{28-2.2\sqrt{7}+1}\) \(=\sqrt{\left(2\sqrt{7}-1\right)^2}=2\sqrt{7}-1\)
Do đó biểu thức đã cho bằng \(\left(3-\sqrt{7}\right)-\left(2\sqrt{7}-1\right)=4-3\sqrt{7}\)
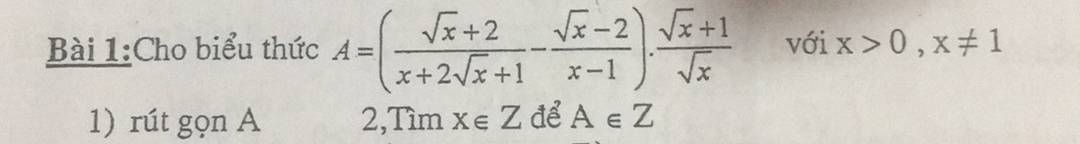
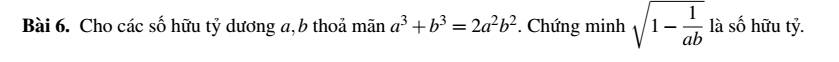
Bài 6 ;mk ko chép lại đề bài nữa nhé
1, p=[1-\(\dfrac{4}{\sqrt{x}+1}+\dfrac{1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)]:\(\dfrac{x-2\sqrt{x}}{x-1}\)
=\(\left[\dfrac{x-1-4\left(\sqrt{x}-1\right)+1}{x-1}\right]:\dfrac{x-2\sqrt{x}}{x-1}\)
=\(\left[\dfrac{x-1-4\sqrt{x}+4+1}{x-1}\right]:\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{x-1}\)
=\(\dfrac{\left(\sqrt{x}-2\right)^2}{x-1}\times\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
=\(\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
b, p=\(\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{x}=4\)
\(\Leftrightarrow x=16\)