Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 3.1:
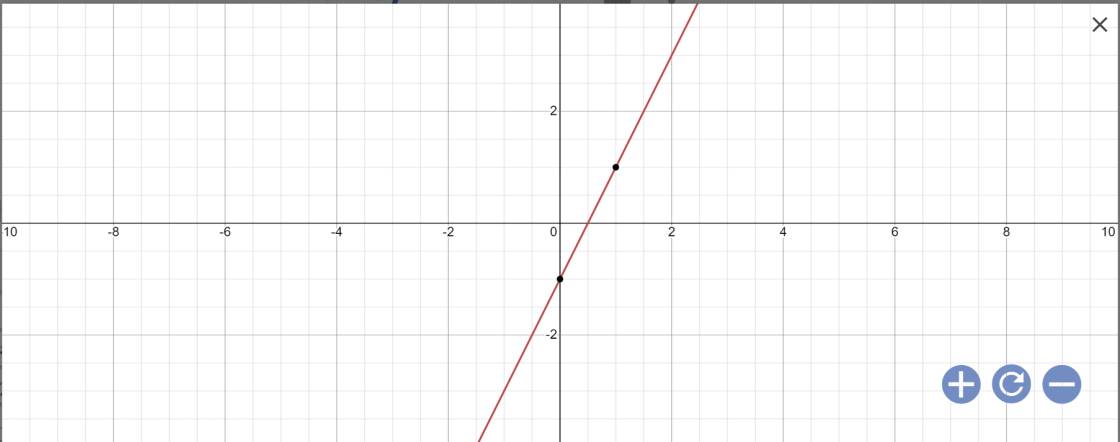
a: Thay x=1 vào y=2x-1, ta được:
\(y=2\cdot1-1=1\)
vậy: A(1;1)
b: Thay y=-3/2 vào y=2x-1, ta được:
\(2x-1=-\dfrac{3}{2}\)
=>\(2x=-\dfrac{1}{2}\)
=>\(x=-\dfrac{1}{4}\)
Vậy: \(B\left(-\dfrac{1}{4};-\dfrac{3}{2}\right)\)
c:
Bài 3.2:
a: Thay m=1 vào (1), ta được:
\(y=\left(-1-2\right)x+1-1=-3x\)
Vẽ đồ thị:
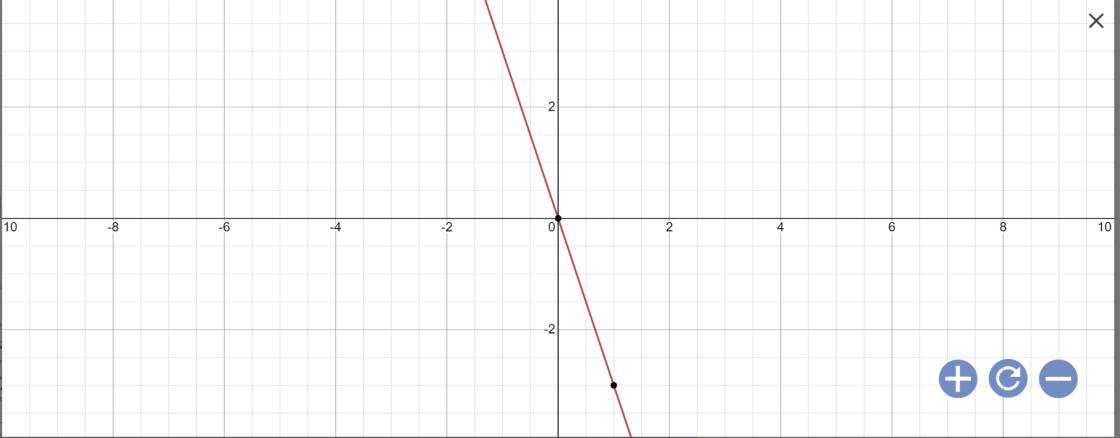
b:
Thay x=2 và y=0 vào (1), ta được:
\(2\left(-m-2\right)+m-1=0\)
=>-2m-4+m-1=0
=>-m-5=0
=>m=-5
c: Thay x=0 và y=2 vào (1), ta được:
\(0\left(-m-2\right)+m-1=2\)
=>m-1=2
=>m=3
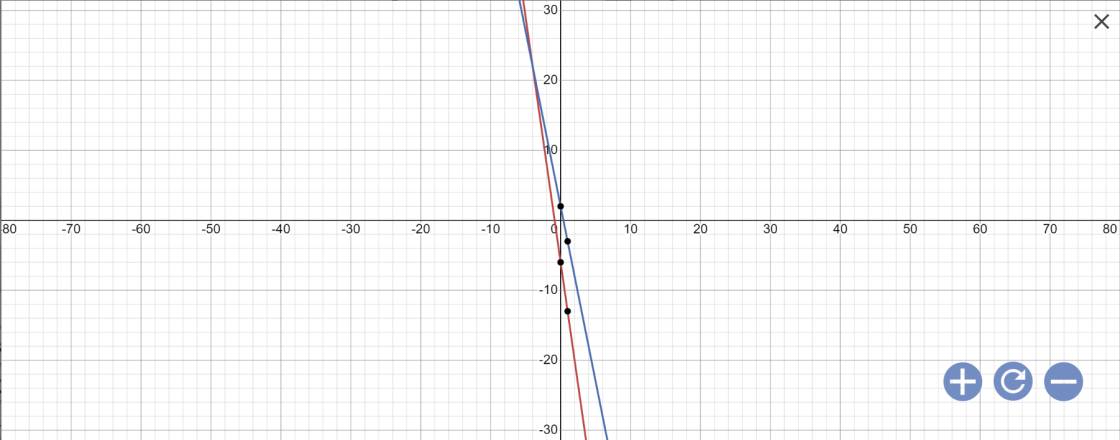
d: Khi m=-5 thì (1): \(y=\left(-5-2\right)x+\left(-5\right)-1=-7x-6\)
Khi m=3 thì (1); \(y=\left(-3-2\right)x+3-1=-5x+2\)
Vẽ đồ thị:
\(\dfrac{3}{x+1}-\dfrac{3x+2}{x^3+1}\)(ĐKXĐ: x<>-1)
\(=\dfrac{3}{x+1}-\dfrac{3x+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{3\left(x^2-x+1\right)-3x-2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{3x^2-3x+3-3x-2}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{3x^2-6x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(m^2(x-1)=2(2x-3)+m\\\Leftrightarrow m^2x-m^2=4x-6+m\\\Leftrightarrow m^2x-4x=m^2+m-6\\\Leftrightarrow (m^2-4)x=(m-2)(m+3)\text{ (1) }\)
+, Xét \(m^2-4=0\Leftrightarrow m=\pm2\)
*) Với \(m=2\) thì pt (1) trở thành:
\(\left(2^2-4\right)x=\left(2-2\right)\left(2+3\right)\)
\(\Leftrightarrow0x=0\) (luôn đúng)
\(\Rightarrow m=2\) thì pt (1) có vô số nghiệm
*) Với \(m=-2\) thì pt (1) trở thành:
\(\left[\left(-2\right)^2-4\right]x=\left(-2-2\right)\left(-2+3\right)\)
\(\Leftrightarrow0x=-4\) (vô lí)
\(\Rightarrow m=-2\) thì pt vô nghiệm
+, Xét \(m^2-4\ne0\Leftrightarrow m\ne\pm2\)
Khi đó, pt (1) tương đương:
\(\left(m-2\right)\left(m+2\right)x=\left(m-2\right)\left(m+3\right)\)
\(\Leftrightarrow x=\dfrac{m+3}{m+2}\) (do \(m\ne\pm2\)) \(\Rightarrow m\ne\pm2\) thì pt có nghiệm \(x=\dfrac{m+3}{m+2}\).
Vậy: ...
Đây là dạng toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp bezout như sau.
\(x^2\) + \(x\) - \(xy\) = 3y + 5
\(x^2\) + \(x\) - 5 = 3y + \(xy\)
\(x^2\) + \(x\) - 5 = y.(3 + \(x\))
y = \(\dfrac{x^2+x-5}{3+x}\) (1); (đk \(x\) ≠ -3)
y \(\in\) Z ⇔ \(x^2\) + \(x\) - 5 ⋮ 3 + \(x\)
Theo bezout ta có:
\(x^2\) + \(x\) - 5 ⋮ 3 + \(x\)
⇔ (-3)2 + (-3) - 5 ⋮ 3 + \(x\)
⇔ 1 ⋮ 3 + \(x\)
3 + \(x\) \(\in\) Ư(1) = {-1; 1}
\(x\) \(\in\) {-4; -2}
Lập bảng ta có:
| \(x\) | - 4 | -2 |
| y = \(\dfrac{x^2+x-5}{3+x}\) | -7 | -3 |
Theo bảng trên ta có: (\(x;y\)) = (-4; -7); (-2; -3)
Vậy (\(x;y\)) = (-4; -7); (-2; -3)
Giải
Số hình lập phương được sơn đúng một mặt là:
(4 - 2) x (4 - 2) x 6 = 24 (hình)
Số hình lập phương có đúng hai mặt được sơn là:
(4 - 2) x 12 = 24 (hình)
Kết luận: a, có 24 hình lập phương nhỏ được sơn đúng một mặt
có 24 hình lập phương nhỏ được sơn đúng hai mặt
a) Ở mỗi mặt, có hình lập phương nhỏ được sơn một mặt (các hình được gạch sọc).
Ở sáu mặt có: (hình).
b) Ở mỗi cạnh, có hình lập phương được sơn hai mặt (các hình ghi dấu "").
Ở cạnh có : (hình).
giúp mình hai câu này với
