Tìm tất cả các nghiệm nguyên của phương trình x5-2x4+2x2-(y2+3)x+2y2-2=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


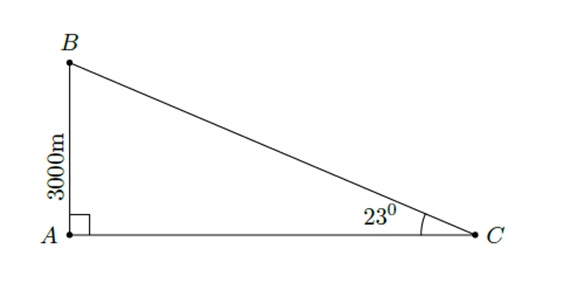
Muốn đạt độ cao 30003000 m so với mặt đất thì máy bay phải bay một đoạn đường dài:
\(BC=\dfrac{AB}{sin\left(23^o\right)}=\dfrac{3000}{sin\left(23^o\right)}\approx7678\left(m\right)\)
Kết luận: Muốn đạt độ cao 30003000 m so với mặt đất thì máy bay phải bay một đoạn đường dài gần 7678m

Tổng giá ban đầu ba sản phẩm bác Đô mua là:
2 200 000 + 1 500 000 + 12 000 000= 15 700 000 (đồng)
Vì hóa đơn trị giá từ 12000000 đồng trở lên thì giảm 12% nên số tiền 3 sản phẩm sau khi giảm giá là:
15 700 000 - 15 700 000.12%= 13 816 000 (đồng)
Vì hóa đơn trị giá từ 12000000 đồng trở lên thì giảm 12% và kèm theo tiền quà tặng 300 000 đồng nên số tiền bác Đô đã phải trả khi mua hàng là:
13 816 000 - 300 000= 13 516 000 (đồng)

a)
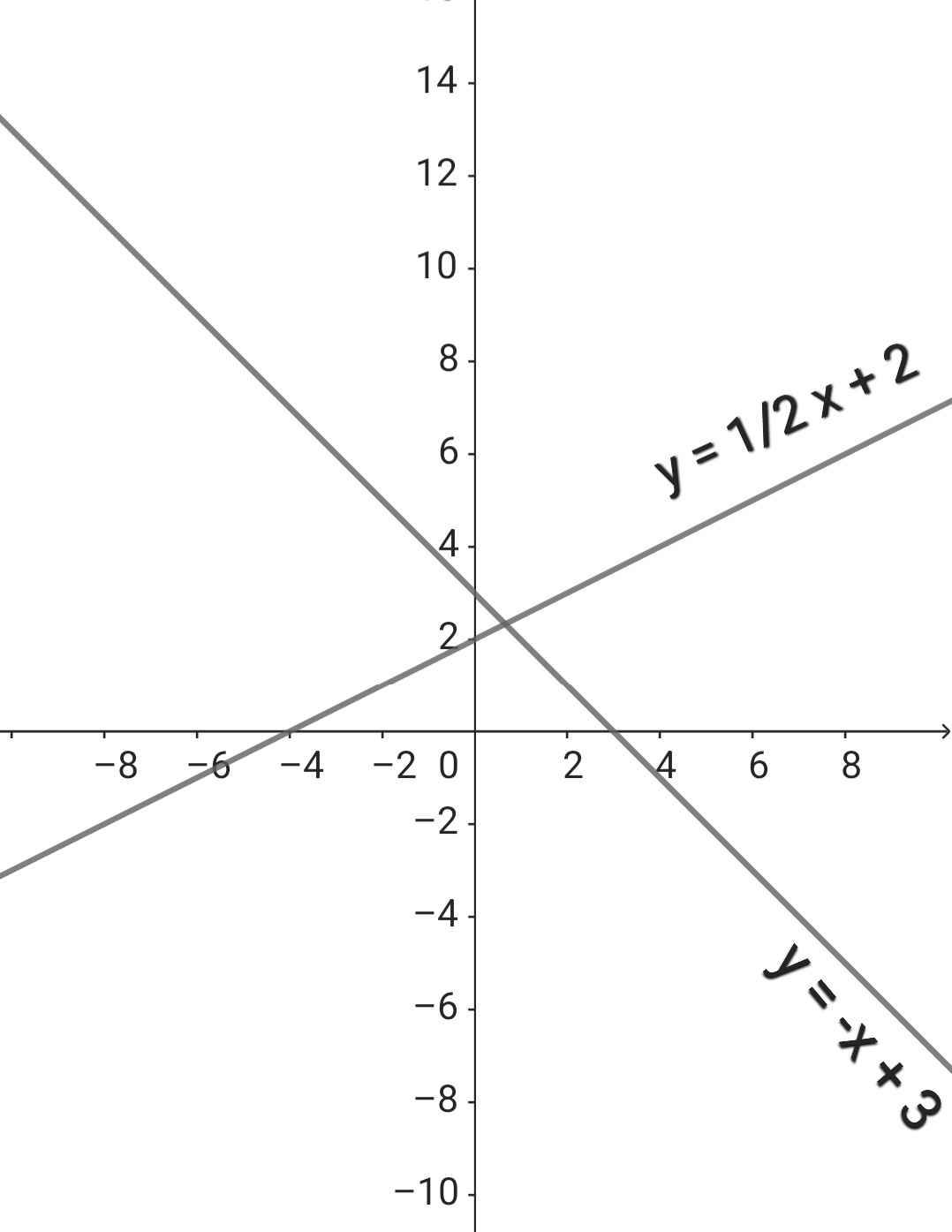 b) Phương trình hoành độ giao điểm của (D₁) và (D₂):
b) Phương trình hoành độ giao điểm của (D₁) và (D₂):
x/2 + 2 = -x + 3
⇔ x/2 + x = 3 - 2
⇔ 3x/2 = 1
⇔ x = 1 : 3/2
⇔ x = 2/3
⇒ y = -2/3 + 3
⇔ y = 7/3
Vậy A(2/3; 7/3)
c) Do (D) // (D₂)
⇒ a = -1
⇒ (D): y = -x + b
Thay x = -2 vào (D₁) ta có:
y = 1/2 . (-2) + 2
⇔ y = 1
Thay x = -2; y = 1 vào (D) ta có:
2 + b = 1
⇔ b = 1 - 2
⇔ b = -1
Vậy (D): y = -x - 1
Bài 3:
a)
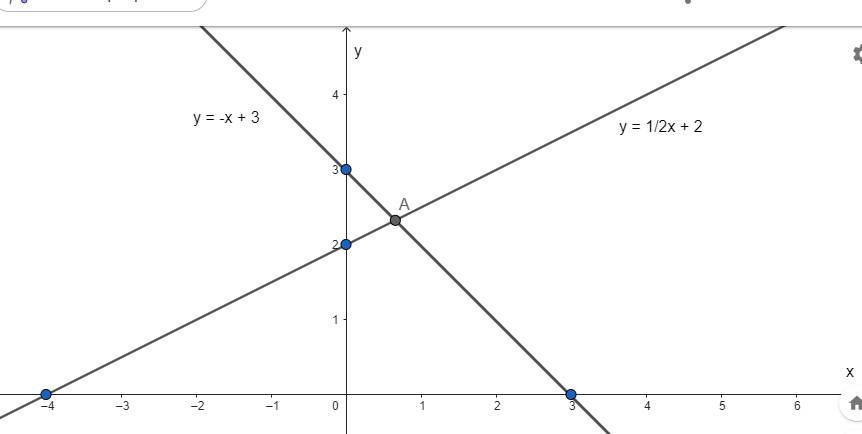
b) Xét phương trình hoành độ giao điểm của D1 và D2 có: y = y
⇒ \(\dfrac{1}{2}x+2=-x+3\)
⇒ \(\dfrac{3}{2}x=1\)
⇒ \(x=\dfrac{2}{3}\)
Thay \(x=\dfrac{2}{3}\) vào D2 có \(y=-\dfrac{2}{3}+3=\dfrac{7}{3}\)
⇒ \(A\left(\dfrac{2}{3};\dfrac{7}{3}\right)\)
Vậy D1 cắt D2 tại \(A\left(\dfrac{2}{3};\dfrac{7}{3}\right)\)
c) ĐK: a ≠ 0
Vì (D) // (D2)
⇒ \(\left\{{}\begin{matrix}a=-1\left(TM\right)\\b\ne3\end{matrix}\right.\)
Vì (D) cắt (D1) tại điểm có hoành độ x = 2
Tức là x = -2 và y = 1
Thay x = 2; y = 0 và a = -1(TMĐK) vào D có:
⇒ \(-2\cdot-1+b=1\)
⇒ \(b+2=1\)
⇒ \(b=-1\left(TM\right)\)
Vậy (D) : y = \(-x-1\)

a) \(\sqrt{ }\)20 + 2\(\sqrt{ }\)45 - 3\(\sqrt{ }\)80 + \(\sqrt{ }\)125
= \(\sqrt{ }\)4.5 +2\(\sqrt{ }\)9.5 - 3\(\sqrt{16.5}\)
= 2\(\sqrt{5}\) + 6\(\sqrt{5}\) - 12\(\sqrt{5}\)
= -4\(\sqrt{5}\)
b) \(\dfrac{2\sqrt{3}+3\sqrt{2}}{\sqrt{3}+\sqrt{2}}\) - \(4\sqrt{\dfrac{3}{2}}\)- \(\dfrac{5}{1-\sqrt{6}}\)
= \(\dfrac{2\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}\)- \(\sqrt{16.\dfrac{3}{2}}\) - \(\dfrac{5\left(1+\sqrt{6}\right)}{\left(1-\sqrt{6}\right)\left(1+\sqrt{6}\right)}\)
= 2 - \(\sqrt{24}\) - \(\dfrac{5\left(1+\sqrt{6}\right)}{1-6}\)
= 2 - \(\sqrt{4.6}\) + 1+\(\sqrt{ }\)6
= 2 - 2\(\sqrt{ }\)6 + 1+\(\sqrt{ }\)6
= 3 - \(\sqrt{ }\)6
c) (đề bài) với x khác 4...
= \(\dfrac{\sqrt{x}}{\sqrt{x}-2}\)- \(\dfrac{4\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
= \(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-2\right)}\)- ....
= \(x-4\sqrt{x}+4\)/ \(\sqrt{x}\left(\sqrt{x}-2\right)\)
= (căn -2)2/ căn x(căn x -2)
= căn x-2/căn x

Lời giải:
Gọi 2 số cần tìm là $a,b$. Theo bài ra ta có:
$a+b=727$
$b=727-a$
$3\times a=7\times b+201$
Thay $b=727-a$ thì:
$3\times a=7\times (727-a)+201$
$3\times a=7\times 727-7\times a+201$
$3\times a=5290-7\times a$
$3\times a+7\times a=5290$
$10\times a=5290$
$a=5290:10=529$
$b=727-529=198$

Vì ƯCLN(a;b) = 12 ⇒ a = 12.k; b = 12.d (k;d) = 1
Theo bài ra ta có: a.b = 12.k.12.d = 12.252
k.d = 12.252: 12:12
k.d = 21
21 = 3.7 ⇒ Ư(21) = {1; 3; 7; 21)
Lập bảng ta có:
| k | 1 | 3 | 7 | 21 |
| d | 21 | 7 | 3 | 1 |
| a = 12k | 12 | 36 | 84 | 252 |
| b = 12d | 252 | 84 | 36 | 12 |
Theo bảng trên ta có:
(a;b) = (12; 252); (36; 84); (84; 36); (252; 12)
Vì 12 < a < b nên (a;b) = (36; 84)
Kết luận: các cặp số tự nhiên a; b thỏa mãn đề bài là: (a;b) = (36; 84)

\(x^5\) - 2\(x^4\) - (y2 + 3)\(x\) + 2y2 - 2 = 0
(\(x^5\) - 2\(x^4\))- (y2 + 3)\(x\) + 2.(y2 + 3) - 8 = 0
\(x^4\).(\(x\) - 2) - (y2 + 3).(\(x\) - 2) - 8 = 0
(\(x\) - 2).(\(x^4\) - y2 - 3) = 8
8 = 23; Ư(8) = {-8; - 4; -2; - 1; 1; 2; 4; 8}
Lập bảng ta có:
vì \(x\); y nguyên nên theo bảng trên ta có các cặp \(x\); y thỏa mãn đề bài là:
(\(x\); y) = (0; -1;); (0; 1)