
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8. Gọi số vé loại I và loại II lần lượt là x và y
ĐK: x,y > 0
Tổng số vé bán được là 500 vé `=> x+y=500` (1)
Tổng số tiền vé bán được là 44500000 đồng nên ta có pt:
`100000x+75000y=44500000`
`<=>4x+3y=1780` (2)
Từ (1) và (2) ta có hpt: \(\left\{{}\begin{matrix}x+y=500\\4x+3y=1780\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=280\\y=220\end{matrix}\right.\left(tm\right)\)
Vậy: ...

\(a)\dfrac{5}{x+7}=\dfrac{-14}{x-5}\left(x\ne-7;x\ne5\right)\\ \Leftrightarrow-14\left(x+7\right)=5\left(x-5\right)\\ \Leftrightarrow-14x-98=5x-25\\ \Leftrightarrow5x+14x=-98+25\\ \Leftrightarrow19x=-73\\ \Leftrightarrow x=-\dfrac{73}{19}\left(tm\right)\\ b)\dfrac{3}{3x-2}=\dfrac{1}{x+1}\left(x\ne\dfrac{2}{3};x\ne-1\right)\\ \Leftrightarrow3\left(x+1\right)=3x-2\\ \Leftrightarrow3x+3=3x-2\\ \Leftrightarrow3=-2\)
=> Pt vô nghiệm
\(c)\dfrac{x}{x-2}=\dfrac{1}{x+1}+1\left(x\ne2;x\ne-1\right)\\ \Leftrightarrow\dfrac{x}{x-2}=\dfrac{x+2}{x+1}\\ \Leftrightarrow x\left(x+1\right)=\left(x-2\right)\left(x+2\right)\\ \Leftrightarrow x^2+x=x^2-4\\ \Leftrightarrow x=-4\left(tm\right)\)
\(d)\dfrac{x+6}{x+5}+\dfrac{3}{2}=2\left(x\ne-5\right)\\ \Leftrightarrow\dfrac{2\left(x+6\right)}{2\left(x+5\right)}+\dfrac{3\left(x+5\right)}{2\left(x+5\right)}=2\\ \Leftrightarrow\dfrac{2\left(x+6\right)+3\left(x+5\right)}{2\left(x+5\right)}=2\\ \Leftrightarrow2x+12+3x+15=4\left(x+5\right)\\ \Leftrightarrow5x+27=4x+20\\ \Leftrightarrow5x-4x=20-27\\ \Leftrightarrow x=-7\left(tm\right)\)
e: ĐKXĐ: x<>3
\(\dfrac{x+5}{x-3}+2=\dfrac{2}{x-3}\)
=>\(\dfrac{x+5+2x-6}{x-3}=\dfrac{2}{x-3}\)
=>3x-1=2
=>3x=3
=>x=1(nhận)
f: ĐKXĐ: \(x\notin\left\{0;-1\right\}\)
\(\dfrac{3x+5}{x+1}+\dfrac{2}{x}=3\)
=>\(\dfrac{3x+3+2}{x+1}+\dfrac{2}{x}=3\)
=>\(\dfrac{2}{x+1}+\dfrac{2}{x}=0\)
=>\(\dfrac{2x+2x+2}{x\left(x+1\right)}=0\)
=>4x+2=0
=>4x=-2
=>\(x=-\dfrac{1}{2}\left(loại\right)\)
g: ĐKXĐ: \(x\notin\left\{3;2\right\}\)
\(\dfrac{x+3}{x-2}+\dfrac{x+2}{x-3}=2\)
=>\(\dfrac{\left(x+3\right)\left(x-3\right)+\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=2\)
=>\(\dfrac{x^2-9+x^2-4}{x^2-5x+6}=2\)
=>\(2\left(x^2-5x+6\right)=2x^2-13\)
=>-10x+12=-13
=>-10x=-25
=>\(x=\dfrac{5}{2}\left(nhận\right)\)
h: ĐKXĐ: \(x\notin\left\{2;3\right\}\)
\(\dfrac{2}{x-2}-\dfrac{3}{x-3}=\dfrac{3x-20}{\left(x-3\right)\left(x-2\right)}\)
=>\(\dfrac{2\left(x-3\right)-3\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{3x-20}{\left(x-3\right)\left(x-2\right)}\)
=>\(2x-6-3x+6=3x-20\)
=>3x-20=-x
=>4x=20
=>x=5(nhận)

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\y>=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}=5\\3\sqrt{x}-\sqrt{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}+3\sqrt{x}-\sqrt{y}=5+1\\2\sqrt{x}+\sqrt{y}=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5\sqrt{x}=6\\\sqrt{y}=5-2\sqrt{x}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=\dfrac{6}{5}\\\sqrt{y}=5-2\cdot\dfrac{6}{5}=5-\dfrac{12}{5}=\dfrac{13}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{36}{25}\\y=\dfrac{169}{25}\end{matrix}\right.\)
=>Chọn B
\(\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}=5\\3\sqrt{x}-\sqrt{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x}=6\\2\sqrt{x}+\sqrt{y}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=\dfrac{6}{5}\\\dfrac{12}{5}+\sqrt{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{36}{25}\\\sqrt{y}=5-\dfrac{12}{5}=\dfrac{13}{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{36}{25}\\y=\left(\dfrac{13}{5}\right)^2=\dfrac{169}{25}\end{matrix}\right.\)
=> Chọn B

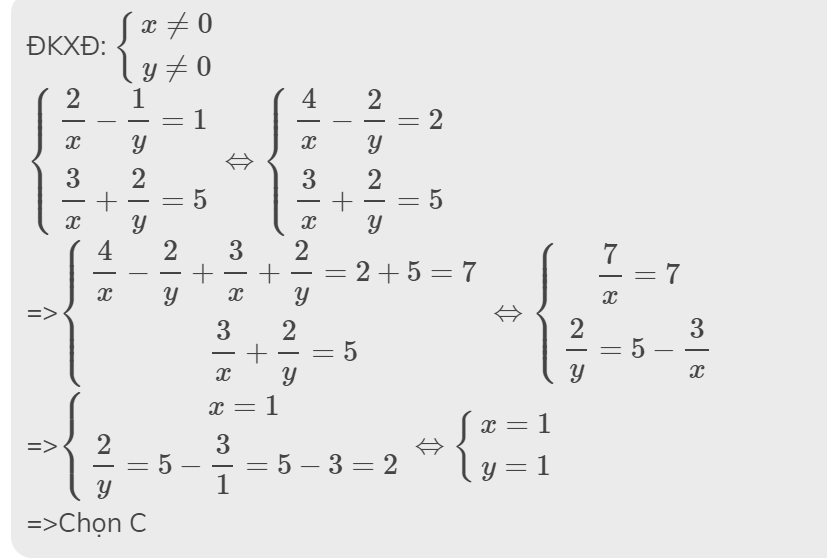
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{1}{y}=1\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}-\dfrac{2}{y}=2\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x}-\dfrac{2}{y}+\dfrac{3}{x}+\dfrac{2}{y}=2+5=7\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{x}=7\\\dfrac{2}{y}=5-\dfrac{3}{x}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\\dfrac{2}{y}=5-\dfrac{3}{1}=5-3=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
=>Chọn C

\(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\\ =\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}\right)^2-2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\\ =\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\\ =\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\\ =2\sqrt{2}\)

Bài 1:
a) Để căn thức có nghĩa thì:
\(x+1\ge0\Leftrightarrow x\ge-1\)
b) Để căn thức có nghĩa thì:
\(3x-8\ge0\Leftrightarrow3x\ge8\Leftrightarrow x\ge\dfrac{8}{3}\)
c) Để căn thức có nghĩa thì:
\(2x^2+3>0\)
Mà điều này luôn đúng nên căn thức có nghĩa khi x ∈ R
d) Để căn thức có nghĩa thì:
\(16-x^2\ge0\Leftrightarrow\left(4-x\right)\left(4+x\right)\ge0\Leftrightarrow-4\le x\le4\)
Câu 1: B
Câu 2: D
Câu 3: ĐKXĐ: 2x+5>=0
=>2x>=-5
=>\(x>=-\dfrac{5}{2}\)
=>Chọn C
Câu 4: ĐKXĐ: 3-4x>=0
=>-4x>=-3
=>4x<=3
=>\(x< =\dfrac{3}{4}\)
=>Chọn D
Câu 5: \(\sqrt{7}-\sqrt{\left(1-\sqrt{7}\right)^2}\)
\(=\sqrt{7}-\left|1-\sqrt{7}\right|\)
\(=\sqrt{7}-\sqrt{7}+1=1\)
=>Chọn B
Câu 6: \(\sqrt{x^2-6x+9}=\sqrt{\left(x-3\right)^2}=\left|x-3\right|\)
x>=3 nên x-3>=0
=>\(\sqrt{x^2-6x+9}=\left|x-3\right|=x-3\)
=>Chọn B
Câu 7: \(\sqrt{25+x^2+10x}=\sqrt{x^2+10x+25}=\sqrt{\left(x+5\right)^2}=\left|x+5\right|\)
x<-6
=>x+6<0
mà x+5<x+6
nên x+5<0
=>\(\sqrt{25+x^2+10x}=-\left(x+5\right)\)
=>Chọn D
Câu 8: \(M=2x-\sqrt{x^4+2x^2+1}\)
\(=2x-\sqrt{\left(x^2+1\right)^2}\)
\(=2x-\left(x^2+1\right)=-\left(x^2-2x+1\right)=-\left(x-1\right)^2\)
Thay x=11 vào M, ta được:
\(M=-\left(11-1\right)^2=-10^2=-100\)
=>Chọn A
Câu 9: \(\sqrt{x-7}=2\)
=>\(x-7=2^2=4\)
=>x=4+7=11
=>Chọn C
Câu 10: \(\sqrt{a^4b^2}=\sqrt{a^4}\cdot\sqrt{b^2}=a^2\cdot\left|b\right|\)
=>Chọn D
Câu 11: \(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=\dfrac{2-\sqrt{3}+2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(=\dfrac{4}{4-3}=4\)
=>Chọn C
Câu 12: A

\(\dfrac{4}{\sqrt{5}+\sqrt{3}}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2}-\sqrt{2^2\cdot5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{5-3}-2\sqrt{5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{2}-2\sqrt{5}\\ =2\left(\sqrt{5}-\sqrt{3}\right)-2\sqrt{5}\\ =2\sqrt{5}-2\sqrt{3}-2\sqrt{5}\\ =-2\sqrt{3}\)

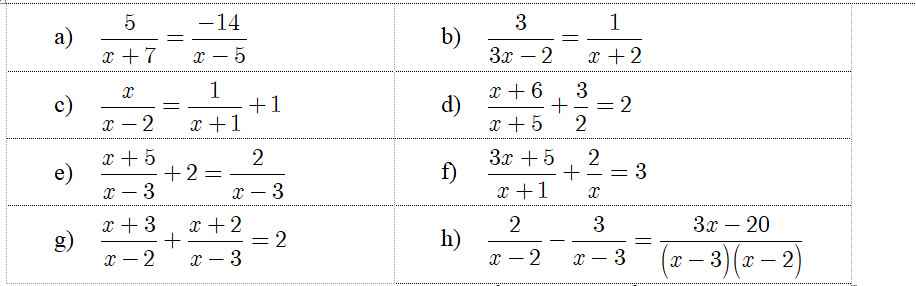
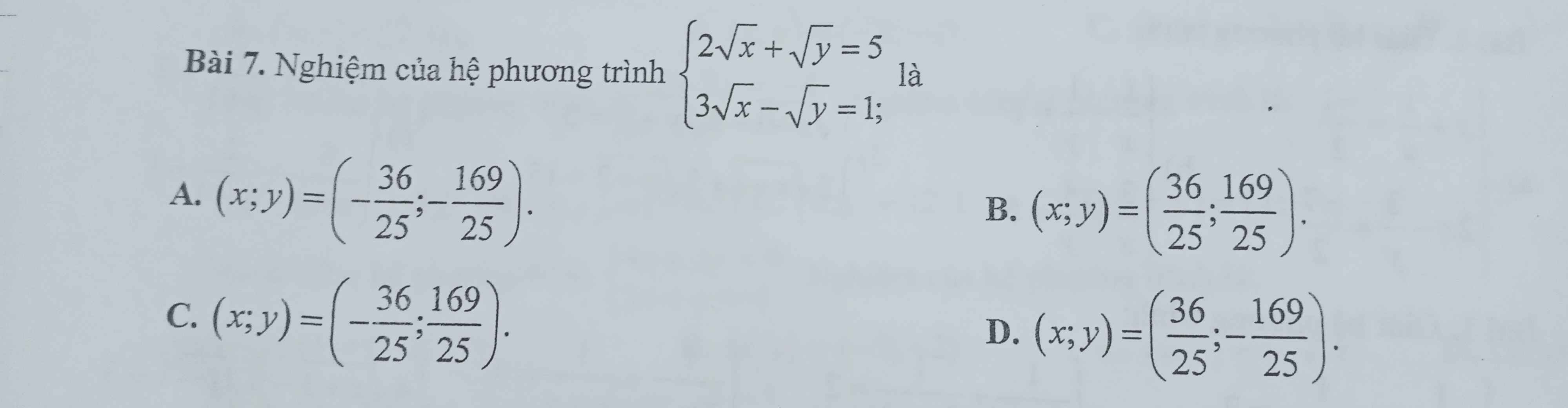
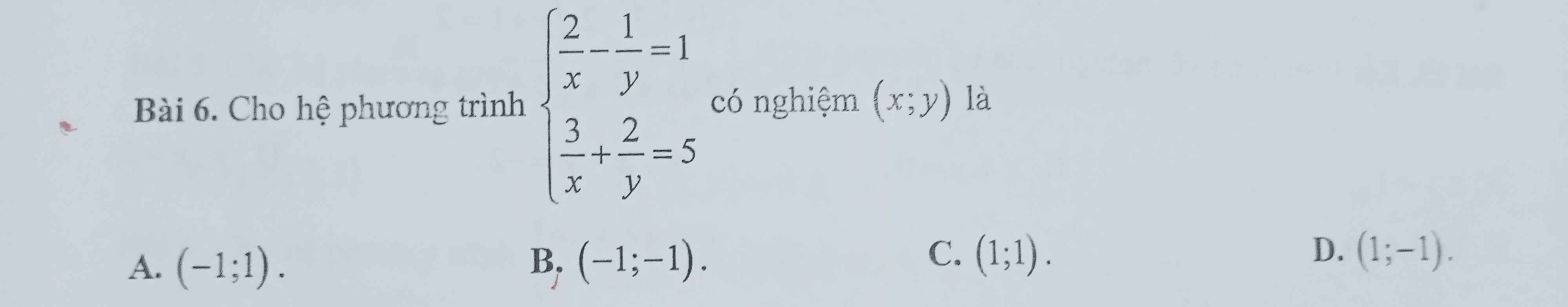
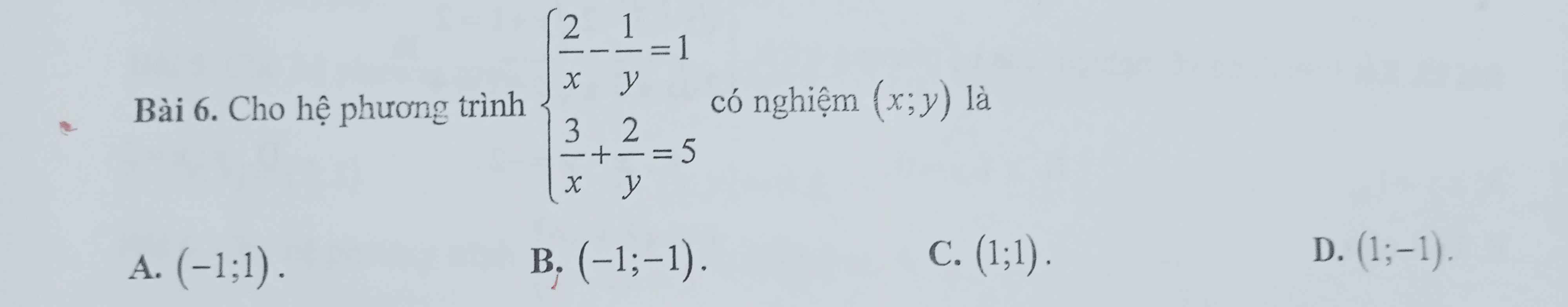
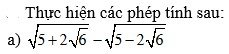

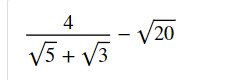
6. Gọi nhóm bạn trẻ có `x` (người)
ĐK: x ∈ N*
Mỗi người góp số tiền là: \(\dfrac{240}{x}\) (triệu)
Sau khi thêm thì tổng số người có trong nhóm là: \(x+2\) (người)
Sau khi thêm thì mỗi người góp: \(\dfrac{240}{x+2}\) (triệu)
Mà sau khi thêm người thì số tiền góp của mỗi người giảm đi 4 triệu nên ta có pt:
\(\dfrac{240}{x}-4=\dfrac{240}{x+2}\\ \Leftrightarrow\dfrac{240}{x}-\dfrac{240}{x+2}=4\\ \Leftrightarrow\dfrac{240\left(x+2\right)-240x}{x\left(x+2\right)}=4\\ \Leftrightarrow\dfrac{480}{x\left(x+2\right)}=4\\ \Leftrightarrow4x\left(x+2\right)=480\\ \Leftrightarrow x\left(x+2\right)=120\\ \Leftrightarrow x^2+2x-120=0\\ \Leftrightarrow\left(x-10\right)\left(x+12\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=10\left(tm\right)\\x=-12\left(ktm\right)\end{matrix}\right.\)
Vậy: ...