Tìm x:
a, \(\sqrt{x+5}-\sqrt{x-3}=2\)
b, \(\sqrt{3x+4}+\sqrt{x+4}=2\sqrt{x}\)
c, \(\sqrt{x^2+x+4}+\sqrt{x^2+x+1}=\sqrt{2x^2+2x+9}\)
d, \(\sqrt[3]{2x-1}+\sqrt[3]{x-1}=\sqrt[3]{3x+1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C K I
Áp dụng định lý hàm cos
\(BC^2=AB^2+AC^2-2.AB.AC.\cos\widehat{A}\) tính được BC
Áp dụng t/c đường phân giác
\(\dfrac{IB}{AB}=\dfrac{IC}{AC}\Rightarrow\dfrac{IB}{IC}=\dfrac{AB}{AC}=\dfrac{6}{12}=\dfrac{1}{2}\) sẽ tính được IB và IC
Áp dụng định lý hàm cos cho tg ABI có
\(IB^2=AB^2+AI^2-2.AB.AI.\cos\widehat{BAI}\) sẽ tính được AI
Bạn tự tính toán nhé!


\(M=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}-\dfrac{6\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+2\sqrt{x}-6\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{x-4\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)
đk x >= 0 ; x khác 1
\(M=\dfrac{x+2\sqrt{x}-6\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)

đk x >= 0 ; x khác 1
\(B=\dfrac{x-5-2\sqrt{x}-2+4\sqrt{x}+4}{x-1}=\dfrac{x+2\sqrt{x}-3}{x-1}=\dfrac{\sqrt{x}+3}{\sqrt{x}+1}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-3\end{matrix}\right.\)
\(x_1^2+2mx_2-x_1-x_2+x_1x_2=6\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)+2mx_2-x_1-x_2=6\)
\(\Leftrightarrow2mx_1+2mx_2-x_1-x_2=6\)
\(\Leftrightarrow2m\left(x_1+x_2\right)-\left(x_1+x_2\right)=6\)
\(\Leftrightarrow\left(2m-1\right)\left(x_1+x_2\right)=6\)
\(\Leftrightarrow2m\left(2m-1\right)=6\)
\(\Leftrightarrow2m^2-m-3=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=\dfrac{3}{2}\end{matrix}\right.\)

- Sửa đề: CMR: M,N,P,Q thẳng hàng.
* AM, AN, AP, AQ cắt BC lần lượt tại F,G,H,I.
- \(\Delta AMB\) và \(\Delta FMB\) có: \(\widehat{AMB}=\widehat{FMB}=90^0;\widehat{ABM}=\widehat{FBM};BM\) là cạnh chung.
\(\Rightarrow\Delta AMB=\Delta FMB\left(g-c-g\right)\)
\(\Rightarrow MA=MF\) nên \(M\) là trung điêm AF.
- Tương tự: N là trung điểm AG, P là trung điểm AH, Q là trung điểm AI.
\(\Rightarrow MN,NP,PQ\) lần lượt là đường trung bình của \(\Delta AFG,\Delta AGH,\Delta AHI\)
\(\Rightarrow MN\)//NP//PQ//BC.
\(\Rightarrow\)M,N,P,Q thẳng hàng.

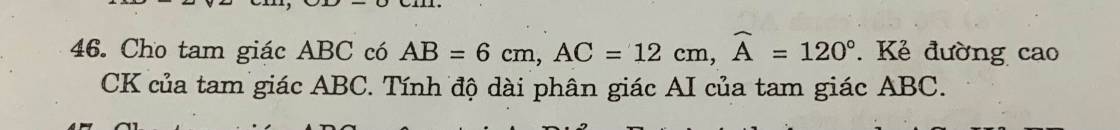
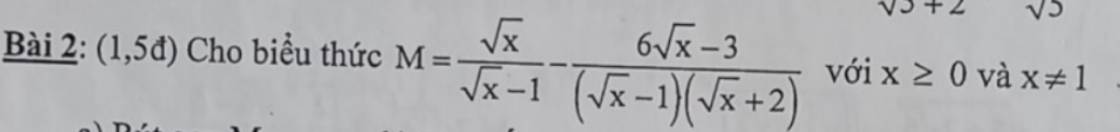


a) đkxđ \(x\ge3\)
Đặt \(\sqrt{x+5}=a\left(a\ge2\sqrt{2}\right)\) và \(\sqrt{x-3}=b\left(b\ge0\right)\). Khi đó pt đã cho \(\Leftrightarrow a-b=2\) (*)
Mặt khác \(a^2-b^2=\left(\sqrt{x+5}\right)^2-\left(\sqrt{x-3}\right)^2\) \(=x+5-\left(x-3\right)=8\), do đó ta có \(a^2-b^2=8\) \(\Leftrightarrow\left(a-b\right)\left(a+b\right)=8\), kết hợp với (*), ta có \(2\left(a+b\right)=8\Leftrightarrow a+b=4\)
Như vậy ta có hpt \(\left\{{}\begin{matrix}a-b=2\\a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=1\end{matrix}\right.\left(nhận\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x+5}=3\\\sqrt{x-3}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+5=9\\x-3=1\end{matrix}\right.\Leftrightarrow x=4\left(nhận\right)\)
Vậy pt đã cho có nghiệm \(x=4\)
b) điều kiện \(x\ge0\)
Đặt \(\sqrt{3x+4}=a\left(a\ge2\right)\), \(\sqrt{x+4}=b\left(b\ge2\right)\) và \(c=\sqrt{x}\left(c\ge0\right)\). Khi đó pt đã cho \(\Leftrightarrow a+b=2c\)
Mặt khác \(b^2-c^2=\left(\sqrt{x+4}\right)^2-\left(\sqrt{x}\right)^2=\left(x+4\right)-x=4\) hay \(b^2-c^2=4\)
và \(3b^2-a^2=3\left(\sqrt{x+4}\right)^2-\left(\sqrt{3x+4}\right)^2\) \(=3\left(x+4\right)-\left(3x+4\right)=8\) hay \(3b^2-a^2=8\)
Vậy ta có hpt \(\left\{{}\begin{matrix}a+b=2c\\3b^2-a^2=8\\b^2-c^2=4\end{matrix}\right.\) (đến đây từ pt 1 ta có \(c=\dfrac{a+b}{2}\), thế vào pt thứ 3 để tìm ra pt thứ 2 theo 2 ẩn a,b, sau đó kết hợp vs pt thứ 2 để giải tìm a, b và đối chiếu điều kiện, từ đó suy ra x.
c) và d) cách làm cũng tương tự a) và b). Đặt ẩn phụ rồi tìm liên hệ giữa các ẩn phụ đó.