
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2a^2+8b^2-8ab\)
\(=2\left(a^2-4ab+4b^2\right)\)
\(=2\left(a-2b\right)^2\)

a2 + b2 + c2 = ab + bc + ca
<=> 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca = 0
<=> (a2 - 2ab + b2) + (b2 - 2ca + c2) + (c2 - 2ac + a2) = 0
<=> (a - b)2 + (b - c)2 + (c - a)2 = 0
Dễ thấy (a - b)2 + (b - c)2 + (c - a)2 \(\ge0\forall a,b,c\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
Mà a + b + c = 2025
nên \(a=b=c=675\)
a2 + b2 + c2 = ab + bc + ca
<=> 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca = 0
<=> (a2 - 2ab + b2) + (b2 - 2ca + c2) + (c2 - 2ac + a2) = 0
<=> (a - b)2 + (b - c)2 + (c - a)2 = 0
Dễ thấy (a - b)2 + (b - c)2 + (c - a)2 ≥0∀�,�,�≥0∀a,b,c
Dấu "=" xảy ra khi {�−�=0�−�=0�−�=0⇔�=�=�⎩⎨⎧a−b=0b−c=0a−c=0⇔a=b=c
Mà a + b + c = 2025
nên �=�=�=675a=b=c=675

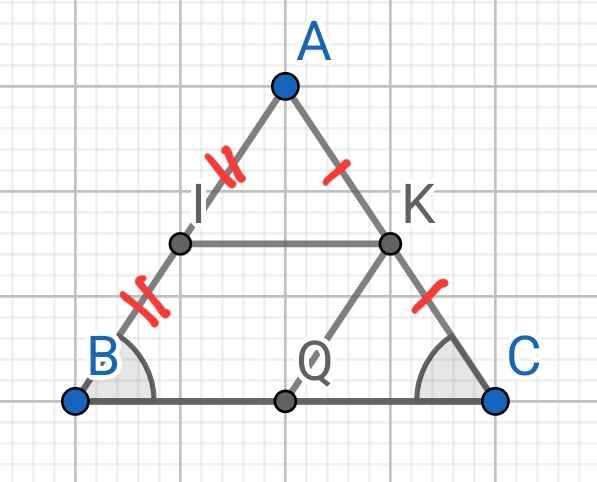
a) Do I là trung điểm AB (gt)
K là trung điểm AC (gt)
⇒ IK là đường trung bình của ∆ABC
⇒ IK // BC
Do ∆ABC cân tại A
⇒ ∠ABC = ∠ACB (hai góc ở đáy)
Tứ giác IKCB có:
IK // BC (cmt)
⇒ IKCB là hình thang
Mà ∠B = ∠C (cmt)
⇒ IKCB là hình thang cân
b) Bổ sung thêm đề ở chỗ KQ // AB (Q ∈ BC)
Do KQ // AB (gt)
⇒ KQ // BI
Lại có IK // BC (cmt)
⇒ IK // BQ
Tứ giác IKQB có:
IK // BQ (cmt)
KQ // BI (cmt)
⇒ IKQB là hình bình hành
c) Do IK là đường trung bình của ∆ABC (cmt)
⇒ IK = BC/2
Mà IKQB là hình bình hành (cmt)
⇒ BQ = IK = BC/2
⇒ Q là trung điểm của BC

13x2 + 9y2 - 30x + 12xy + 25 = 0
<=> (9y2 + 12xy + 4y2) + (9x2 - 30x + 25) = 0
<=> (3y + 2x)2 + (3x - 5)2 = 0
Dễ thấy \(\left(3y+2x\right)^2\ge0;\left(3x-5\right)^2\ge0\forall x,y\)
nên \(\left(3y+2x\right)^2+\left(3x-5\right)^2\ge0\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}3y+2x=0\\3x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{10}{9}\\x=\dfrac{5}{3}\end{matrix}\right.\)

1) \(f\left(x\right)=-3x^2-12x+5\)
\(\Rightarrow f\left(x\right)=-3\left(x^2+4x\right)+5\)
\(\Rightarrow f\left(x\right)=-3\left(x^2+4x+4\right)+5+12\)
\(\Rightarrow f\left(x\right)=-3\left(x+2\right)^2+17\le17\left(-3\left(x+2\right)^2\le0,\forall x\right)\)
\(\Rightarrow GTLN\left(f\left(x\right)\right)=17\left(tạix=-2\right)\)
2) \(f\left(x\right)=-8x^2+20x\)\
\(\Rightarrow f\left(x\right)=-8\left(x^2+\dfrac{5}{2}x\right)\)
\(\Rightarrow f\left(x\right)=-8\left(x^2+\dfrac{5}{2}x+\dfrac{25}{16}\right)+\dfrac{25}{2}\)
\(\Rightarrow f\left(x\right)=-8\left(x+\dfrac{5}{4}\right)^2+\dfrac{25}{2}\le\dfrac{25}{2}\left(-8\left(x+\dfrac{5}{4}\right)^2\le0,\forall x\right)\)
\(\Rightarrow GTLN\left(f\left(x\right)\right)=\dfrac{25}{2}\left(tạix=-\dfrac{5}{4}\right)\)

1) \(f\left(x\right)=6x^2-15x+4\)
\(\Rightarrow f\left(x\right)=6\left(x^2-\dfrac{5}{3}x\right)+4\)
\(\Rightarrow f\left(x\right)=6\left(x^2-\dfrac{5}{3}x+\dfrac{25}{36}-\dfrac{25}{36}\right)+4\)
\(\Rightarrow f\left(x\right)=6\left(x^2-\dfrac{5}{3}x+\dfrac{25}{36}\right)+4-\dfrac{25}{6}\)
\(\Rightarrow f\left(x\right)=6\left(x-\dfrac{5}{6}\right)^2-\dfrac{1}{6}\ge-\dfrac{1}{6}\left(6\left(x-\dfrac{5}{6}\right)^2\ge0,\forall x\right)\)
\(\Rightarrow GTNN\left(f\left(x\right)\right)=-\dfrac{1}{6}\left(tạix=\dfrac{5}{6}\right)\)
2) \(f\left(x\right)=4x^2-13x+5\)
\(\Rightarrow f\left(x\right)=4\left(x^2-\dfrac{13}{4}x\right)+5\)
\(\Rightarrow f\left(x\right)=4\left(x^2-\dfrac{13}{4}x+\dfrac{169}{64}-\dfrac{169}{64}\right)+5\)
\(\Rightarrow f\left(x\right)=4\left(x^2-\dfrac{13}{4}x+\dfrac{169}{64}\right)+5-\dfrac{169}{16}\)
\(\Rightarrow f\left(x\right)=4\left(x-\dfrac{13}{8}\right)^2-\dfrac{89}{16}\ge-\dfrac{89}{16}\left(4\left(x-\dfrac{13}{8}\right)^2\ge0,\forall x\right)\)
\(\Rightarrow GTNN\left(f\left(x\right)\right)=-\dfrac{89}{16}\left(tạix=\dfrac{13}{8}\right)\)

A= (\(x-y\))2 - (y-z)2
A = (\(x-y\) - y + z)(\(x-y\) + y - z)
A = ( \(x\) - 2y + z)(\(x-z\))


Lời giải:
a. $E, F$ là trung điểm của $AB, AC$
$\Rightarrow EF$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow EF\parallel BC$
$\Rightarrow EFCB$ là hình thang
Mà $\widehat{B}=\widehat{C}$ (do $ABC$ cân tại $A$)
$\Rightarrow EFCB$ là hình thang cân.
b. Vì $EFCB$ là htc nên $EC=BF$
Vì $E,F$ là trung điểm $AB,AC$ và $AB=AC$ nên:
$EB=AB:2=AC:2=FC$
Xét tam giác $EBC$ và $FCB$ có:
$EB=FC$
$BC$ chung
$EC=FB$ (cmt)
$\Rightarrow \triangle EBC=\triangle FCB$ (c.c.c)
$\Rightarrow \widehat{ECB}=\widehat{FBC}$
Hay $\widehat{OCB}=\widehat{OBC}$
$\Rightarrow OBC$ là tam giác cân.
c. Xét tam giác $AOB$ và $AOC$ có:
$AO$ chung
$AB=AC$
$OB=OC$ (do tam giác $OBC$ cân tại $O$)
$\Rightarrow \triangle AOB=\triangle AOC$ (c.c.c)
$\Rightarrow \widehat{BAO}=\widehat{CAO}$
$\Rightarrow AO$ là phân giác $\widehat{A} (1)$
Mặt khác: Tam giác $ABC$ cân tại $A$ nên trung tuyến AM đồng thời là phân giác $AM$ của góc $\widehat{A}(2)$
Từ $(1), (2)\Rightarrow A,O,M$ thẳng hàng.
Hình vẽ: