Tính giá trị của M= 1 + \(\dfrac{6}{2x5}\) + \(\dfrac{10}{5x10}\) + \(\dfrac{14}{10x17}\) + \(\dfrac{18}{17x26}\)
giúp mình với các bạn ơi
ghi cả cách giải ra nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: \(\dfrac{1}{x}\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)=\dfrac{1}{99}+\dfrac{2}{98}+\dfrac{3}{97}+...+\dfrac{97}{3}+\dfrac{98}{2}+\dfrac{99}{1}\)
=>\(\dfrac{1}{x}\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)=\left(\dfrac{1}{99}+1\right)+\left(\dfrac{2}{98}+1\right)+...+\left(\dfrac{98}{2}+1\right)+1\)
=>\(\dfrac{1}{x}\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)=\dfrac{100}{99}+\dfrac{100}{98}+...+\dfrac{100}{2}+\dfrac{100}{100}\)
=>\(\dfrac{1}{x}\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)=100\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)\)
=>\(\dfrac{1}{x}=100\)
=>x=1/100

Gọi \(d=ƯC\left(2n+1;4n-2\right)\)
Do \(2n+1\) lẻ \(\Rightarrow d\) lẻ
Ta có: \(\left\{{}\begin{matrix}2n+1⋮d\\4n-2⋮d\end{matrix}\right.\)
\(\Rightarrow2\left(2n+1\right)-\left(4n-2\right)⋮d\)
\(\Rightarrow4⋮d\Rightarrow\left[{}\begin{matrix}d=1\\d=2\\d=4\end{matrix}\right.\)
Mà d lẻ \(\Rightarrow d=1\)
\(\Rightarrow\dfrac{2n+1}{4n-2}\) tối giản

d; \(\dfrac{2x-1}{12}\) = \(\dfrac{5}{3}\)
2\(x\) - 1 = \(\dfrac{5}{3}\).12
2\(x\) - 1 = 20
2\(x\) = 20 + 1
2\(x\) = 21
\(x\) = 21 : 2
\(x=\dfrac{21}{2}\)
Vậy \(x=\dfrac{21}{2}\)
e; \(\dfrac{x}{3}\) - \(\dfrac{1}{4}\) = \(\dfrac{-5}{6}\)
\(\dfrac{x}{3}\) = \(\dfrac{-5}{6}\) + \(\dfrac{1}{4}\)
\(\dfrac{x}{3}\) = - \(\dfrac{7}{12}\)
\(x\) = - \(\dfrac{7}{12}\) x 3
\(x\) = - \(\dfrac{7}{4}\)
Vậy \(x\) = - \(\dfrac{7}{4}\)


b; \(\dfrac{2}{3}\) + \(\dfrac{5}{6}\): 5 - \(\dfrac{1}{18}\).(-3)2
= \(\dfrac{2}{3}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{18}\).9
= \(\dfrac{5}{6}\) - \(\dfrac{1}{2}\)
= \(\dfrac{1}{3}\)
c; \(\dfrac{1}{2}\) + \(\dfrac{-1}{6}\) + \(\dfrac{-1}{12}\) + \(\dfrac{-1}{20}\) + \(\dfrac{-1}{30}\) + \(\dfrac{-1}{42}\)
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\))
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}-\dfrac{1}{7}\))
= \(\dfrac{1}{2}\) - (\(\dfrac{1}{2}\) - \(\dfrac{1}{7}\))
= \(\dfrac{1}{2}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{7}\)
= \(\dfrac{1}{7}\)

Vì A là trung điểm của OM nên
OM = 2OA = 7 x 2 = 14 (cm)
Vì B là trung điểm của ON nên
ON = 2OB = 11 x 2 = 22 (cm)
MN = ON - OM = 22 - 14 = 8 (cm)
Bạn tham khảo:
Để tính độ dài MN, ta sử dụng định lí về trung điểm:
Nếu A là trung điểm của OM và B là trung điểm của ON, thì AB sẽ là đường chính giữa của hình chữ nhật O AMN. Vì AB là đường chính giữa, nên AB sẽ cắt MN tại trung điểm C.
Do đó, ta có MN = 2 X MC
Ta cần tính độ dài MC. Vì M là trung điểm của OA, nên MC = 1/2 OA
Từ đây, ta có:
MC = 1/2 OA = 1/2 7cm = 3.5cm
Do đó:
MN = 2 x MC = 2 x 3.5 = 7cm
Vậy, độ dài MN là 7cm
#hoctot

\(M=1+2.\left(\dfrac{3}{2.5}+\dfrac{5}{5.10}+\dfrac{7}{10.17}+\dfrac{9}{17.26}\right)\)
\(=1+2\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{17}+\dfrac{1}{17}-\dfrac{1}{26}\right)\)
\(=1+2\left(\dfrac{1}{2}-\dfrac{1}{26}\right)\)
\(=1+1-\dfrac{1}{13}=\dfrac{25}{13}\)

Đặt \(A=\dfrac{1}{2^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}\)
\(=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\right)\)
Đặt \(B=1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{50^2}< \dfrac{1}{49\cdot50}=\dfrac{1}{49}-\dfrac{1}{50}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
=>\(B=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}< 2-\dfrac{1}{50}\)
=>\(A=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\right)< \dfrac{1}{2^2}\left(2-\dfrac{1}{50}\right)=\dfrac{1}{2}-\dfrac{1}{200}< \dfrac{1}{2}\)
\(\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}\right)^2+\left(\dfrac{1}{6}\right)^2+...+\left(\dfrac{1}{100}\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}.\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}.\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{2}.\dfrac{1}{50}\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2.\left[1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2\right]\)
Ta có:
\(\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2.2}< \dfrac{1}{2.1}=\dfrac{2-1}{2.1}=\dfrac{2}{2.1}-\dfrac{1}{2.1}=1-\dfrac{1}{2}\)
\(\left(\dfrac{1}{3}\right)^2=\dfrac{1}{3.3}< \dfrac{1}{3.2}=\dfrac{3-2}{3.2}=\dfrac{3}{3.2}-\dfrac{2}{3.2}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\left(\dfrac{1}{50}\right)^2=\dfrac{1}{50.50}< \dfrac{1}{50.49}=\dfrac{50-49}{50.49}=\dfrac{50}{50.49}-\dfrac{49}{50.49}=\dfrac{1}{49}-\dfrac{1}{50}\)
Khi đó
\(1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2< 1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}=2-\dfrac{1}{50}< 2\)
\(=\left(\dfrac{1}{2}\right)^2.\left[1+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2+...+\left(\dfrac{1}{50}\right)^2\right]< \dfrac{1}{4}.2=\dfrac{1}{2}\)
Vậy \(\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{4}\right)^2+\left(\dfrac{1}{6}\right)^2+...+\left(\dfrac{1}{100}\right)^2< \dfrac{1}{2}\left(đpcm\right)\)
Tick cho mk nha :>>

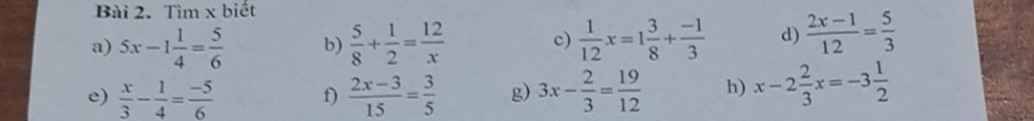
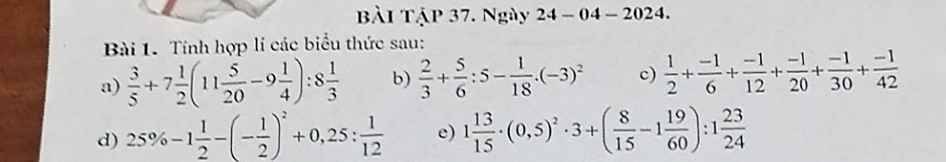
\(M=1+\dfrac{6}{2\cdot5}+\dfrac{10}{5\cdot10}+\dfrac{14}{10\cdot17}+\dfrac{18}{17\cdot26}\)
\(=1+2\left(\dfrac{3}{2\cdot5}+\dfrac{5}{5\cdot10}+\dfrac{7}{10\cdot17}+\dfrac{9}{17\cdot26}\right)\)
\(=1+2\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{17}+\dfrac{1}{17}-\dfrac{1}{26}\right)\)
\(=1+2\left(\dfrac{1}{2}-\dfrac{1}{26}\right)=1+2\cdot\dfrac{12}{26}=1+\dfrac{24}{26}=\dfrac{50}{26}=\dfrac{25}{13}\)