Giúp câu c,d,e với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
17 tháng 3 2024
a) B(x) = 3x² - x³ + 2x² + 4x - 5 + 2x³
= (3x² + 2x²) + (-x³ + 2x³) + 4x - 5
= 5x² + x³ + 4x - 5
=> Vậy, đa thức B(x) sau khi thu gọn là B(x) = x³ + 5x² + 4x - 5.
b) Bậc của đa thức B(x) là 3 và hệ số cao nhất của đa thức B(x) là 1.
AH
Akai Haruma
Giáo viên
17 tháng 3 2024
Lời giải:
a. $B(x)=(-x^3+2x^3)+(3x^2+2x^2)+4x-5$
$=x^3+5x^2+4x-5$
b.
Bậc của đa thức: $3$
Hệ số cao nhất: $1$ (chính là hệ số gắn với $x^3$)
LP
1
17 tháng 3 2024
+ P(2) = 1: Thay x = 2 vào P(x) ta có: a.2 + b = 1
+ P(-1) = -5: Thay x = -1 vào P(x) ta có: a.(-1) + b = -5
Ta có:
3a = 6
=> a = 2
Thay a = 2 vào a.2 + b = 1, ta có:
2.2 + b = 1
=> b = -3
Vậy: a = 2; b = -3
LP
2
KV
17 tháng 3 2024
P(3) = 3² - 6.3 + 9 = 9 - 18 + 9 = 0
P(-3) = (-3)² - 6.(-3) + 9 = 9 + 18 + 9 = 36
P(-1) = (-1)² - 6.(-1) + 9 = 1 + 6 + 9 = 16
17 tháng 3 2024
Sửa đề: AE=1/3AC
Ta có: AE+EC=AC
=>\(EC+\dfrac{1}{3}AC=AC\)
=>\(CE=\dfrac{2}{3}CA\)
Vì AM và AB là hai tia đối nhau
nên A nằm giữa M và B
mà MA=AB
nên A là trung điểm của MB
Xét ΔMBC có
CA là đường trung tuyến
\(CE=\dfrac{2}{3}CA\)
Do đó: E là trọng tâm cuả ΔMBC
Xét ΔMBC có
E là trọng tâm
BE cắt MC tại H
Do đó: H là trung điểm của MC
NV
0
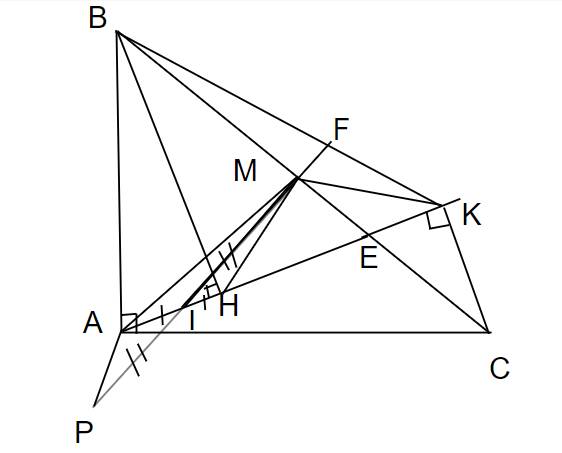
c: Ta có: ΔAEM vuông tại A
=>\(\widehat{AEM}< 90^0\)
mà \(\widehat{CEM}+\widehat{AEM}=180^0\)(hai góc kề bù)
nên \(\widehat{CEM}>90^0\)
Xét ΔCEM có \(\widehat{CEM}>90^0\)
nên CM là cạnh lớn nhất trong ΔCEM
=>CM>ME
e: Xét ΔCAB có AD là phân giác
nên \(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{1}{2}\)
=>CD=2BD