giá trị vô tỉ của phương trình x^5-16x^3=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a\left(ax+1\right)\text{=}x\left(a+2\right)+2\)
\(\Leftrightarrow a^2x-ax-2x\text{=}2-a\)
\(\Leftrightarrow x\left(a^2-a-2\right)\text{=}2-a\)
\(\Leftrightarrow x\left(a+1\right)\left(a-2\right)\text{=}2-a\)
\(\Leftrightarrow x\text{=}\dfrac{-1}{a+1}\)
em mới có lớp 8 nên là em không chắc nữa

*Đường tròn ngoại tiếp tam giác AEJ cắt JF tại K (K khác J).
\(\Rightarrow AJKE\) nội tiếp nên \(\widehat{EKF}=\widehat{JAF}\) (vì \(\widehat{EKF}\) là góc ngoài đỉnh K của tg AJKE).
Xét △EKF và △JAF có: \(\widehat{JFA}\) là góc chung, \(\widehat{EKF}=\widehat{JAF}\).
\(\Rightarrow\)△EKF∼△JAF (g-g).
\(\Rightarrow\dfrac{FE}{JF}=\dfrac{FK}{FA}\Rightarrow FE.FA=FK.FJ\left(1\right)\)
Ta có: A,C,B,E cùng thuộc (O) \(\Rightarrow AEBC\) nội tiếp.
Nên \(\widehat{JAE}=\widehat{JBC}\) (vì \(\widehat{JAE}\) là góc ngoài đỉnh A của tg AEBC).
Mà \(\widehat{JBC}+\widehat{EBF}=180^0\Rightarrow\widehat{JAE}+\widehat{EBF}=180^0\)
\(\Rightarrow\widehat{EKF}+\widehat{EBF}=180^0\) mà \(\widehat{EKF}+\widehat{EKJ}=180^0\)
\(\Rightarrow\widehat{JKE}=\widehat{JBF}\)
Xét △JEK và △JFB có: \(\widehat{JKE}=\widehat{JFB}\), \(\widehat{BJF}\) là góc chung.
\(\Rightarrow\)△JEK∼△JFB (g-g).
\(\Rightarrow\dfrac{JK}{JB}=\dfrac{JE}{JF}\Rightarrow JE.JB=JK.JF\left(2\right)\)
\(\left(1\right)+\left(2\right)\Rightarrow FE.FA+JE.JB=JF\left(JK+JK\right)=JK^2\left(đpcm\right)\)

y = \(\sqrt{2x}\) + 3 ( đk x ≥ 0)
y = 2 ⇔ \(\sqrt{2x}\) + 3 = 2 ⇔ \(\sqrt{2x}\) = 2 - 3 ⇔ \(\sqrt{2x}\) = -1 (vô lý)
Vậy x \(\in\) \(\varnothing\)

ĐKXĐ: a > 0 và a khác 1
\(P=\dfrac{2\left(a^2+2\right)}{\left(1-a\right)\left(1+a+a^2\right)}-\dfrac{\left(1-\sqrt{a}\right)\left(1+a+a^2\right)}{\left(1-a\right)\left(1+a+a^2\right)}-\dfrac{\left(1+\sqrt{a}\right)\left(1+a+a^2\right)}{\left(1-a\right)\left(1+a+a^2\right)}\)\(=\dfrac{2a^2+4-\left(1+a+a^2\right).\left(1-\sqrt{a}+1+\sqrt{a}\right)}{1-a^3}\)
\(=\dfrac{2a^2+4-\left(1+a+a^2\right)}{1-a^3}\)
\(=\dfrac{a^2+a+3}{\left(1-a^3\right)}\)
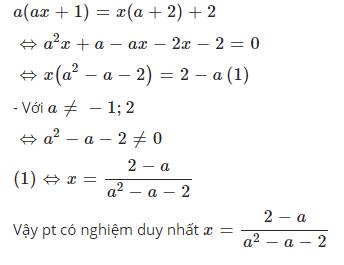
\(x^5-16x^3=0\)
\(\Leftrightarrow x^3.\left(x^2-16\right)=0\)
\(\Leftrightarrow x^3.\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)