
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(A\left(x\right)=2x^3-6x^2-5\left(x^2-2x-5\right)\)
\(=2x^3-6x^2-5x^2+10x+25\)
\(=2x^3-11x^2+10x+25\)
\(B\left(x\right)=x^3-3\left(x^3-2x^2-5x\right)\)
\(=x^3-3x^3+6x^2+15x\)
\(=-2x^3+6x^2+15x\)
b: \(A\left(x\right)=2x^3-11x^2+10x+25\)
Bậc là 2
Hệ số cao nhất là 2
Hệ số tự do là 25
c: A(x)-C(x)=B(x)
=>C(x)=A(x)-B(x)
\(=2x^3-11x^2+10x+25+2x^3-6x^2-15x\)
\(=4x^3-17x^2-5x+25\)
d: Đặt P(x)=0
=>B(x)+2x3=0
=>\(-2x^3+6x^2+15x+2x^3=0\)
=>\(6x^2+15x=0\)
=>3x(2x+5)=0
=>x(2x+5)=0
=>\(\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)

-108 ko thể được số nào mũ 2 được nhé vì âm nhân âm = dương và dương nhân dương= dương

a: Xét ΔDBA vuông tại D và ΔABC vuông tại A có
\(\widehat{DBA}\) chung
Do đó: ΔDBA~ΔABC
b: ΔDBA~ΔABC
=>\(\dfrac{BD}{BA}=\dfrac{BA}{BC}\left(1\right)\)
Xét ΔBAD có BF là phân giác
nên \(\dfrac{BD}{BA}=\dfrac{FD}{FA}\left(2\right)\)
Xét ΔBAC có BE là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AE}{EC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{FD}{FA}=\dfrac{AE}{EC}\)
=>\(FD\cdot EC=AE\cdot FA\)

a: \(\left(\dfrac{1}{4}+\dfrac{-3}{11}\right)+\left(\dfrac{2}{11}+\dfrac{-8}{11}+\dfrac{3}{4}\right)\)
\(=\dfrac{1}{4}+\dfrac{-3}{11}+\dfrac{2}{11}+\dfrac{-8}{11}+\dfrac{3}{4}\)
\(=\left(\dfrac{1}{4}+\dfrac{3}{4}\right)-\dfrac{9}{11}=1-\dfrac{9}{11}=\dfrac{2}{11}\)
b: \(\left(-1\dfrac{1}{3}+1\dfrac{1}{2}\right)+2\dfrac{1}{2}\)
\(=-1-\dfrac{1}{3}+1+\dfrac{1}{2}+2+\dfrac{1}{2}\)
\(=2+1-\dfrac{1}{3}=3-\dfrac{1}{3}=\dfrac{8}{3}\)
c: \(\left(-2\dfrac{1}{4}\right)+\dfrac{5}{2}:3\dfrac{3}{4}\)
\(=-\dfrac{9}{4}+\dfrac{5}{2}:\dfrac{15}{4}\)
\(=-\dfrac{9}{4}+\dfrac{5}{2}\cdot\dfrac{4}{15}=\dfrac{-9}{4}+\dfrac{2}{3}\)
\(=\dfrac{-27+8}{12}=-\dfrac{19}{12}\)
d: \(\dfrac{5}{8}:0,25-\left(0,6-2\dfrac{1}{4}\right):2\dfrac{1}{5}\)
\(=\dfrac{5}{8}:\dfrac{1}{4}-\left(\dfrac{3}{5}-\dfrac{9}{4}\right):\dfrac{11}{5}\)
\(=\dfrac{5}{2}-\dfrac{12-45}{20}\cdot\dfrac{5}{11}\)
\(=\dfrac{5}{2}-\dfrac{5}{20}\cdot\dfrac{-33}{11}=\dfrac{5}{2}+\dfrac{3}{4}=\dfrac{13}{4}\)
e: \(1\dfrac{1}{2}\cdot1\dfrac{1}{3}\cdot...\cdot1\dfrac{1}{999}\)
\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{1000}{999}\)
\(=\dfrac{1000}{2}=500\)
f: \(\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-99}{100}=-\dfrac{1}{100}\)

e: Chiều dài hình chữ nhật là: \(\dfrac{4y^2+4y-3}{2x-1}\left(cm\right)\)
f: Chiều rộng của hình hộp là:
\(\dfrac{3x^3+8x^2-45x-40}{\left(x+5\right)\left(x+1\right)}\)
\(=\dfrac{3x^3+8x^2-45x-40}{x^2+6x+5}\)
\(=\dfrac{3x^3+18x^2+15x-10x^2-60x-50+10}{x^2+6x+5}\)
\(=3x-10+\dfrac{10}{x^2+6x+5}\left(cm\right)\)

a: Thể tích của bể nước là:
\(2\cdot1,5\cdot1,2=3,6\left(m^3\right)=3600\left(lít\right)\)
b: thể tích nước đã chảy vào bể là:
4x600=2400(lít)=2,4m3
Chiều cao của mực nước là:
2,4:2:1,5=1,2:1,5=0,8(m)


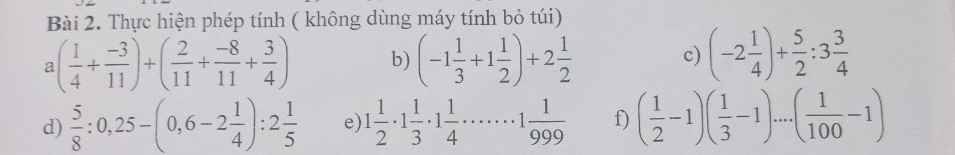


a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔEBC=ΔDCB
b: Ta có: ΔEBC=ΔDCB
=>\(\widehat{ECB}=\widehat{DBC}\)
=>\(\widehat{HBC}=\widehat{HCB}\)
=>ΔHBC cân tại H
Xét ΔBHC có HB+HC>BC
=>BC<2BH
=>\(BH>\dfrac{BC}{2}\)