Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM\(\perp\)BC và AM là phân giác của \(\widehat{BAC}\)

Gọi O là trung điểm của AD

=>O là tâm đường tròn đường kính AD

Vì \(\widehat{AHD}=\widehat{AMD}=\widehat{AKD}=90^0\)

nên A,H,D,M,K cùng thuộc đường tròn đường kính AD

=>A,H,D,M,K cùng thuộc (O)

Xét (O) có

\(\widehat{MHK}\) là góc nội tiếp chắn cung MK

\(\widehat{MAK}\) là góc nội tiếp chắn cung MK

Do đó: \(\widehat{MHK}=\widehat{MAK}\)(2)

Xét (O) có

\(\widehat{MKH}\) là góc nội tiếp chắn cung MH

\(\widehat{MAH}\) là góc nội tiếp chắn cung MH

Do đó: \(\widehat{MKH}=\widehat{MAH}\left(2\right)\)

Ta có: AM là phân giác của góc BAC

=>\(\widehat{BAM}=\widehat{CAM}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\widehat{MHK}=\widehat{MKH}\)

=>ΔMHK cân tại M

=>MH=MK

Đặt f(x)=0

=>2x-2+6=0

=>2x+4=0

=>2x=-4

=>x=-2

a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}+52^0=90^0\)

=>\(\widehat{ABC}=38^0\)

b: Xét ΔMAB vuông tại A và ΔMCD vuông tại C có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

Do đó: ΔMAB=ΔMCD

c: Ta có: ΔMAB=ΔMCD

=>MB=MD

Xét ΔMAD và ΔMCB có

MA=MC

\(\widehat{AMD}=\widehat{CMB}\)(hai góc đối đỉnh)

MD=MB

Do đó: ΔMAD=ΔMCB

=>\(\widehat{MAD}=\widehat{MCB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AD//BC

d: ta có: ΔMAB=ΔMCD

=>AB=CD

mà \(BI=IA=\dfrac{BA}{2};CK=KD=\dfrac{CD}{2}\)

nên BI=IA=CK=KD

Xét ΔMAI vuông tại A và ΔMCK vuông tại C có

MA=MC

AI=CK

Do đó; ΔMAI=ΔMCK

=>\(\widehat{AMI}=\widehat{CMK}\)

mà \(\widehat{AMI}+\widehat{IMC}=180^0\)(hai góc kề bù)

nên \(\widehat{IMC}+\widehat{KMC}=180^0\)

=>I,M,K thẳng hàng

a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔBAD=ΔBHD

b: ta có: ΔBAD=ΔBHD

=>DA=DH

Xét ΔDAK vuông tại A và ΔDHC vuông tại H có

DA=DH

\(\widehat{ADK}=\widehat{HDC}\)(hai góc đối đỉnh)

Do đó: ΔDAK=ΔDHC

=>DK=DC

=>ΔKDC cân tại D

c: Ta có: ΔBAD=ΔBHD

=>BA=BH

Ta có: ΔDAK=ΔDHC

=>AK=HC

Xét ΔBKC có \(\dfrac{BA}{AK}=\dfrac{BH}{HC}\)

nên AH//KC

Sửa đề: x-y=20

5x=9y

=>\(\dfrac{x}{9}=\dfrac{y}{5}\)

mà x-y=20

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{9}=\dfrac{y}{5}=\dfrac{x-y}{9-5}=\dfrac{20}{4}=5\)

=>\(x=5\cdot9=45;y=5\cdot5=25\)

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

AB=AC

\(\widehat{BAD}\) chung

Do đó: ΔADB=ΔAEC

b: Ta có: ΔADB=ΔAEC

=>AD=AE

Xét ΔAEI vuông tại E và ΔADI vuông tại D có

AI chung

AE=AD

Do đó: ΔAEI=ΔADI

=>\(\widehat{EAI}=\widehat{DAI}\)

=>\(\widehat{BAI}=\widehat{CAI}\)

=>AI là đường phân giác của ΔABC

c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)

nên ED//BC

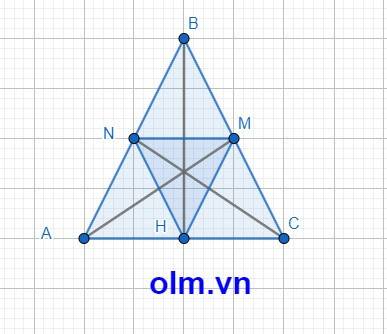
Tam giác MNH đều khi và chỉ HM = HN = MN

Xét tam giác vuông HAB có: HN = \(\dfrac{1}{2}\) AB (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)

Xét tam giác vuông HBC có: HM = \(\dfrac{1}{2}\) BC (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)

  AB = BC (gt) 

⇒ HN = HM  = \(\dfrac{1}{2}\) AB = \(\dfrac{1}{2}\) BC 

Mặt khác ta có : NA = NB; MB = MC nên MN là đường trung bình tam giác ABC

⇒ MN = \(\dfrac{1}{2}\) AC (đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và bằng một nửa cạnh còn lại)

⇒ HN = HM = MN ⇔ \(\dfrac{1}{2}\) AB = \(\dfrac{1}{2}\) BC = \(\dfrac{1}{2}\) AC

⇔ AB = BC = AC

⇔ \(\Delta\)ABC là tam giác đều

Kết luận:  Để tam giác MNH là tam giác đều thì tam giác ABC phải là tam giác đều. 

Cô ơi lớp 7 chưa học đường trung bình ạ