Bài 2: Cho ∆ABC vuông ở A, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
a) Tính góc ADB.
b) Chứng minh tam giác ABD = tam giác BAC.
c) Chứng minh AM = 1/2BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}=90^0\)
=>DE\(\perp\)BC tại E
Xét ΔBEI vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBI}\) chung
Do đó: ΔBEI=ΔBAC
=>BI=BC
=>ΔBIC cân tại B

Câu 3:
a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
b: ΔAIB=ΔAIC
=>\(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC
mà I là trung điểm của BC
nên AI là đường trung trực của BC
c: Xét ΔABC có
AI,BD là các đường trung tuyến
AI cắt BD tại G
Do đó: G là trọng tâm của ΔABC
=>BG=2GD
mà BG>BI(ΔGIB vuông tại I)
nên BI<2GD
Bài 2:
a: \(\dfrac{1}{2}x^2\left(-3x^4+5x^3+6x\right)\)
\(=-\dfrac{1}{2}x^2\cdot3x^4+\dfrac{1}{2}x^2\cdot5x^3+\dfrac{1}{2}x^2\cdot6x\)
\(=-\dfrac{3}{2}x^6+\dfrac{5}{2}x^5+3x^3\)
b: \(\left(x-3\right)\left(2x+5\right)\)
\(=2x^2+5x-6x-15\)
\(=2x^2-x-15\)
c: \(\dfrac{\left(16y^4-20y^3+24y^2\right)}{4y^2}\)
\(=\dfrac{16y^4}{4y^2}-\dfrac{20y^3}{4y^2}+\dfrac{24y^2}{4y^2}\)
\(=4y^2-5y+6\)
d: \(\dfrac{16x^4-1}{4x^2+1}=\dfrac{\left(4x^2-1\right)\left(4x^2+1\right)}{4x^2+1}=4x^2-1\)

a: \(2x\left(5-3x\right)+2x\left(3x-5\right)-3\left(x-7\right)=3\)
=>\(10x-6x^2+6x^2-10x-3x+21=3\)
=>-3x=-18
=>x=6
b: \(3x\left(x+1\right)-2x\left(x+2\right)=-x-1\)
=>\(3x^2+3x-2x^2-4x=-x-1\)
=>\(x^2-x+x+1=0\)
=>\(x^2+1=0\)(vô lý)
=>\(x\in\varnothing\)

Bài 3:
a: \(A\left(x\right)=2x^4-5x^3+7x-5+4x^3+3x^2+2x+3\)
\(=2x^4+\left(-5x^3+4x^3\right)+3x^2+\left(7x+2x\right)-5+3\)
\(=2x^4-x^3+3x^2+9x-2\)
\(B\left(x\right)=5x^4-3x^3+5x-3x^4-2x^3+9-6x\)
\(=\left(5x^4-3x^4\right)+\left(-3x^3-2x^3\right)+\left(5x-6x\right)+9\)
\(=2x^4-5x^3-x+9\)
b: \(A\left(x\right)+B\left(x\right)=2x^4-x^3+3x^2+9x-2+2x^4-5x^3-x+9\)
\(=4x^4-6x^3+3x^2+10x+7\)
\(A\left(x\right)-B\left(x\right)=2x^4-x^3+3x^2+9x-2-2x^4+5x^3+x-9\)
\(=4x^3+3x^2+10x-11\)
c: \(C\left(x\right)=x^4+4x^2+5\)
\(=x^2\left(x^2+4\right)+5>=5\forall x\)
=>C(x)>0 với mọi x
=>C(x) không có nghiệm
Bài 4:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
mà \(\widehat{DHA}=\widehat{HAC}\)(AD//HC)
nên \(\widehat{DAH}=\widehat{DHA}\)
=>ΔDAH cân tại D
=>DA=DH
c: Ta có: \(\widehat{DHA}+\widehat{DHB}=\widehat{AHB}=90^0\)
\(\widehat{DAH}+\widehat{DBH}=90^0\)(ΔAHB vuông tại H)
mà \(\widehat{DHA}=\widehat{DAH}\)
nên \(\widehat{DHB}=\widehat{DBH}\)
=>DB=DH
=>DB=DA
=>D là trung điểm của AB
Xét ΔABC có
CD,AH là các đường trung tuyến
CD cắt AH tại G
Do đó: G là trọng tâm của ΔABC
Xét ΔABC có
G là trọng tâm
E là trung điểm của AC
Do đó: B,G,E thẳng hàng

a: \(A\left(x\right)=3x^3+2x^2+x-4x^2-6\)
\(=3x^3+\left(2x^2-4x^2\right)+x-6\)
\(=3x^3-2x^2+x-6\)
\(B\left(x\right)=-3x^3-3x+2x^2+6x-2\)
\(=-3x^3+2x^2+\left(6x-3x\right)-2\)
\(=-3x^3+2x^2+3x-2\)
b: M(x)=A(x)+B(x)
\(=3x^3-2x^2+x-6-3x^3+2x^2+3x-2\)
=4x-8
Đặt M(x)=0
=>4x-8=0
=>4x=8
=>x=2
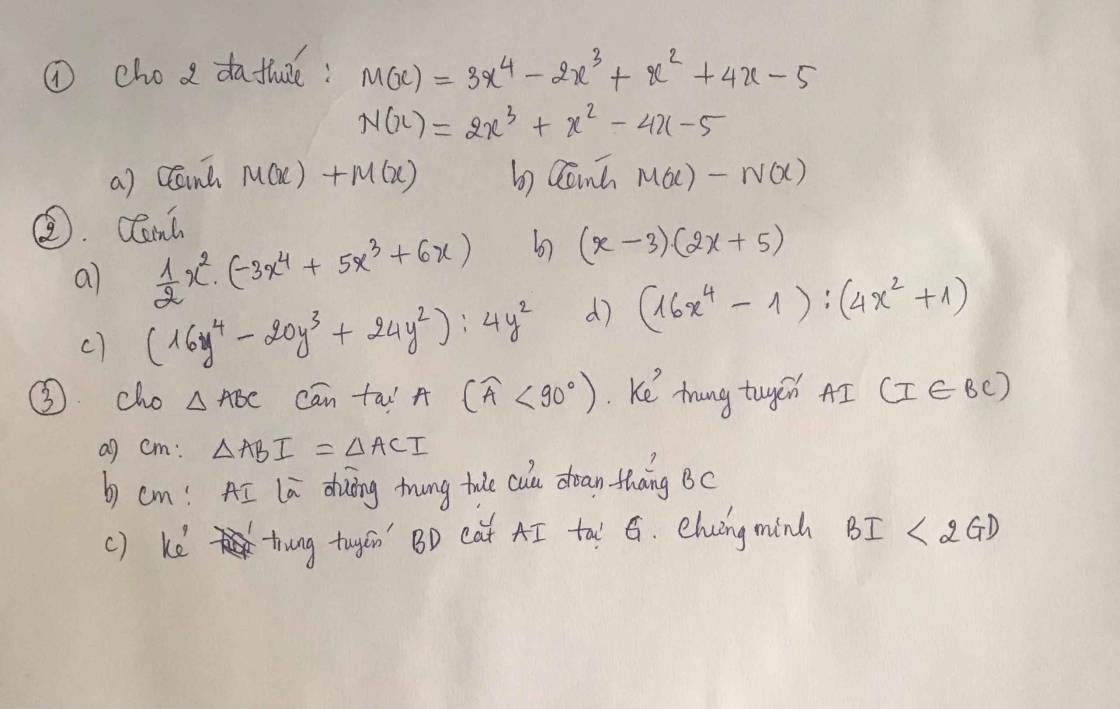

a:
Sửa đề: Tính góc ABD
Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//DB
mà AC\(\perp\)AB
nên DB\(\perp\)AB
=>\(\widehat{DBA}=90^0\)
b: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
Xét ΔABD vuông tại B và ΔBAC vuông tại A có
BA chung
BD=AC(ΔMBD=ΔMCA)
Do đó: ΔABD=ΔBAC
c: Ta có: ΔABD=ΔBAC
=>AD=BC
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)