
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



M=(a+b)(a2-ab+b2)+3ab(1-2ab)+6a2b2
M=a2-ab+b2+3ab
M=(a+b)2=1



\(A=\dfrac{x^2-6x+9}{3}=\dfrac{\left(x-3\right)^2}{3}=\dfrac{1}{3}\left(x-3\right)^2\\ Mà:\left(x-3\right)^2\ge0\forall x\in R\Rightarrow\dfrac{1}{3}\left(x-3\right)^2\ge0\forall x\in R\\ Vậy:min_A=0\Leftrightarrow x=3\\ --\\ B=\dfrac{1}{x^2+10x+25}=\dfrac{1}{\left(x+5\right)^2}\left(ĐKXĐ:x\ne-5\right)\\ Mà:\left(x+5\right)^2\ge0\forall x\in R\\\Rightarrow B_{max}\Leftrightarrow\left(x+5\right)^2min\Leftrightarrow\left(x+5\right)=0\Leftrightarrow x=-5\left(loại\right)\)
Vậy KXĐ giá trị lớn nhất của B và giá trị biến x lúc đó

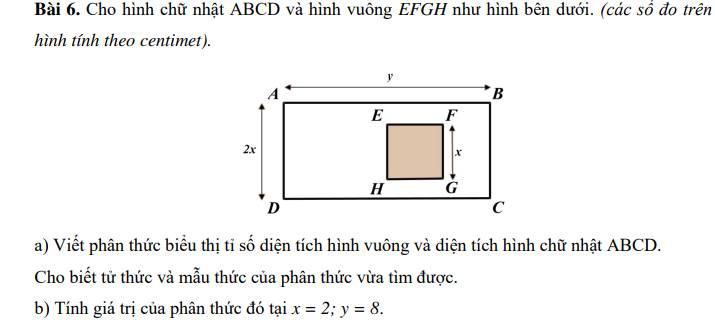
a) Phân thức biểu thị tỉ số diện tích của hình vuông và diện tích hình chữ nhật:
x²/(2xy)
Tử thức là x²
Mẫu thức là 2xy
b) Tại x = 2; y = 8
2²/(2.2.8) = 1/8

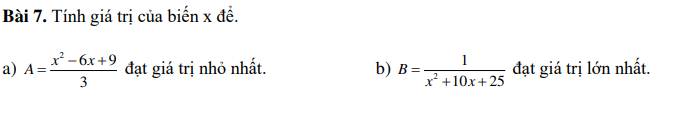
AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
Lại có:
MN ⊥ AH (gt)
⇒ MN // BC
Tứ giác BCMN có:
MN // BC (cmt)
⇒ BCMN là hình thang
b) Do MN // BC (cmt)
⇒ ∠NMB = ∠MBC (so le trong)
Do BM là tia phân giác của ∠ABC (gt)
⇒ ∠ABM = ∠MBC
⇒ ∠NBM = ∠MBC
Mà ∠NMB = ∠MBC (cmt)
⇒ ∠NBM = ∠NMB
∆BMN có:
∠NBM = ∠NMB (cmt)
⇒ ∆BMN cân tại N
⇒ BN = MN