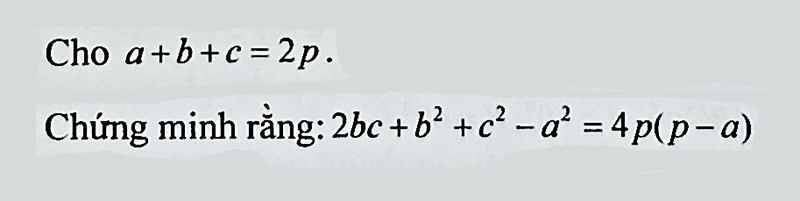
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Do AB < AC (gt)
⇒ ∠C < ∠B (quan hệ giữa góc và cạnh đối diện trong tam giác)
b) Xét hai tam giác vuông: ∆ABM và ∆EBM có:
AB = BE (gt)
BM là cạnh chung
⇒ ∆ABM = ∆EBM (cạnh huyền - cạnh góc vuông)
c) Do ME ⊥ BC (gt)
⇒ NE ⊥ BC
⇒ NE là đường cao của ∆BCN
Do ∆ABC vuông tại A (gt)
⇒ CA ⊥ AB
⇒ CA ⊥ NB
⇒ CA là đường cao thứ hai của ∆BCN
Mà M là giao điểm của NE và CA
⇒ BM là đường cao thứ ba của ∆BCN
⇒ BM ⊥ NC

\(C\left(x\right)=x^3-2x=0\)
\(\Rightarrow x\left(x^2-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^2-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^2=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\pm\sqrt{2}\end{matrix}\right.\)
Vậy nghiệm của đa thức là ...

a: ΔMNQ vuông tại N
=>MQ là cạnh huyền
=>MN<MQ
b: ΔMNP vuông tại N
=>MP là cạnh huyền
=>NP<MP

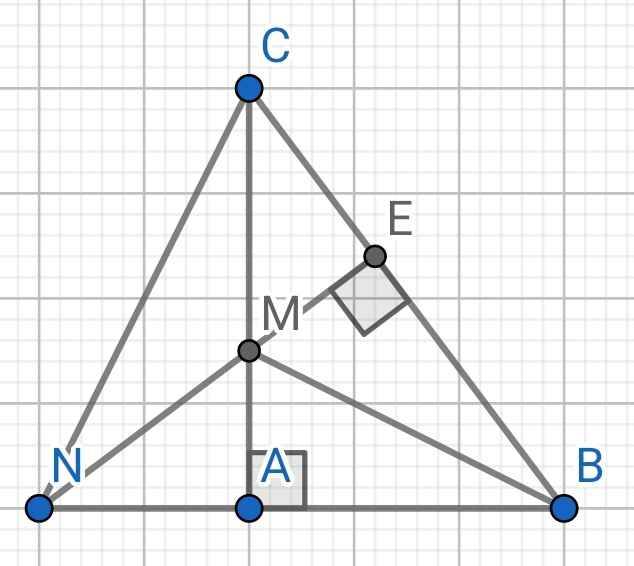
a: Xét ΔABC vuông tại A và ΔAEC vuông tại A có
AB=AE
AC chung
Do đó: ΔABC=ΔAEC
b: Xét ΔCME và ΔCNB có
CM=CN
\(\widehat{MCE}\) chung
CE=CB
Do đó: ΔCME=ΔCNB
=>ME=NB
c:
Ta có: AB=AE
mà A nằm giữa B và E
nên A là trung điểm của BE
Xét ΔCEB có
CA là đường trung tuyến
G là trọng tâm
Do đó: C,G,A thẳng hàng

\(N=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
\(=x^2\left(x+y\right)-2x^2-y\left(x+y\right)+3y+x-1\)
\(=2x^2-2x^2-2y+3y+x-1\)
=x+y-1
=2-1
=1


`a+b+c=2p <=> a^2+b^2+c^2+2(ab+bc+ca)=4p^2`.
`4p(p-a) = 4p^2 - 4pa = a^2+b^2+c^2+2(ab+bc+ca) - 2a(a+b+c)`
`= a^2+b^2+c^2 + 2ab+2bc+2ca-2a^2- 2ab - 2ac`
`= b^2+c^2-a^2+2bc.`