cho tam giác mnp cân tại m (m<900 độ) kẻ góc vuông nh mp (h thuộc mp) pk⊥ mn (k thuộc mn) nh và pk cắt nhau tại E a chứng minh: tam giác mhp = pkn b chứng minh: tam giác enp cân c chứng minh: me là đường phân giác của nmp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(A=\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\)
Khi x=-2 và y=1/3 thì \(A=4\cdot\left(-2\right)^2-\left(\dfrac{1}{3}\right)^2=16-\dfrac{1}{9}=\dfrac{143}{9}\)
b: x(3x-2)-3x2=3/4
=>\(3x^2-2x-3x^2=\dfrac{3}{4}\)
=>\(-2x=\dfrac{3}{4}\)
=>\(x=-\dfrac{3}{4}:2=-\dfrac{3}{8}\)

a: Xét ΔBAH và ΔBIH có
BA=BI
AH=IH
BH chung
Do đó: ΔBAH=ΔBIH
b: Ta có: ΔBAH=ΔBIH
=>\(\widehat{ABE}=\widehat{IBE}\)
Xét ΔBAE và ΔBIE có
BA=BI
\(\widehat{ABE}=\widehat{IBE}\)
BE chung
Do đó: ΔBAE=ΔBIE
=>EA=EI
c: Ta có: ΔBAE=ΔBIE
=>\(\widehat{BAE}=\widehat{BIE}\)
=>\(\widehat{BIE}=90^0\)
=>EI\(\perp\)BC tại I
ta có: EA=EI
mà EA<EM(ΔEAM vuông tại A)
nên EM>EI

a: Xét ΔABC có
AM,BN,CP là các đường trung tuyến
AM,BN,CP cắt nhau tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BN;CG=\dfrac{2}{3}CP;AG=\dfrac{2}{3}AM;AG=2GM\)
=>BG=2GN; CG=2GP
Xét tứ giác BGCQ có
M là trung điểm chung của BC và GQ
=>BGCQ là hình bình hành
=>BQ=CG=2/3CP; BG=CQ=2/3BN
Ta có: AG=2GM
mà GQ=2GM
nên GQ=GA
=>\(GQ=\dfrac{2}{3}AM\)
=>Δcác cạnh của tam giác BQG=2/3 độ dài của các đưòng trung tuyến của tam giác ABC
b: Sửa đề: BM<1/2(BG+BQ)
Xét ΔGBC có GB+GC>BC
=>GB+BQ>2BM
=>\(BM< \dfrac{1}{2}\left(BG+BQ\right)\)
c: Ta có: AG=GQ
=>G là trung điểm của AQ
Các đường trung tuyến của ΔBCQ là GK,QI,BM
Xét ΔQAB có
K,G lần lượt là trung điểm của QB,QA
=>KG là đường trung bình của ΔQAB
=>KG=1/2AB
Ta có: I là trung điểm của BG
=>BI=IG=BG/2
mà GN=BG/2
nên BI=IG=GN
=>G là trung điểm của IN
Xét tứ giác ANQI có
G là trung điểm chung của AQ và NI
=>ANQI là hình bình hành
=>\(QI=AN=\dfrac{AC}{2}\)
Vì M là trung điểm của BC
nên \(BM=\dfrac{1}{2}BC\)
=>ĐPCM

a: Để A(x) có bậc là 2 thì a-5=0
=>a=5
b: Đặt B(x)=0
=>x+1=0
=>x=-1
a: Để A(x) có bậc là 2 thì a-5=0
=>a=5
b: Đặt B(x)=0
=>x+1=0
=>x=-1


\(x^2-9x+20=0\)
=>\(x^2-4x-5x+20=0\)
=>x(x-4)-5(x-4)=0
=>(x-4)(x-5)=0
=>\(\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
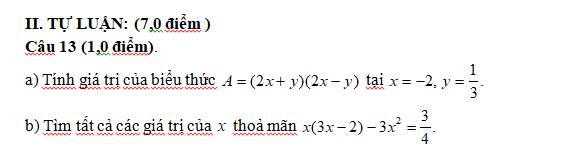




a: Xét ΔKNP vuông tại N và ΔHPN vuông tại H có
NP chung
\(\widehat{KNP}=\widehat{HPN}\)
Do đó: ΔKNP=ΔHPN
b: Ta có;ΔKNP=ΔHPN
=>\(\widehat{KPN}=\widehat{HNP}\)
=>\(\widehat{ENP}=\widehat{EPN}\)
=>ΔENP cân tại E
c: Xét ΔMNE và ΔMPE có
MN=MP
EN=EP
ME chung
Do đó: ΔMNE=ΔMPE
=>\(\widehat{NME}=\widehat{PME}\)
=>ME là phân giác của góc NMP