Tìm GTNN của biểu thức \(y=\frac{x}{2}+\frac{2}{x-1}\) với x>1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

VN
1

NM
Nguyễn Minh Quang
Giáo viên
9 tháng 1 2021
Ta có
\(a^2+b^2+c^2\ge2\left(ab+bc-ac\right)\Leftrightarrow\text{ }a^2+b^2+c^2+2ac-2ab-2bc\ge0\)
\(\Leftrightarrow\left(a+c\right)^2+b^2-2b\left(a+c\right)\ge0\)
\(\Leftrightarrow\left(a+c-b\right)^2\ge0\) luôn đúng
đấu bằng xảy ra khi "a+c-b=0
KM
0

LG
0

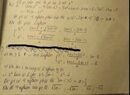

\(\frac{x}{2}+\frac{2}{x-1}\)\(=\frac{x-1}{2}\)\(+\frac{2}{x-1}\)\(+\frac{1}{2}\)\(\ge\sqrt{\frac{x-1}{2}.\frac{2}{x-1}}\)\(+\frac{1}{2}\)\(=...\)
copy nhớ ghi nguồn + viết đầy đủ nhé :))
\(y=\frac{x}{2}+\frac{2}{x-1}=\frac{x-1+1}{2}+\frac{2}{x-1}\)
\(=\frac{x-1}{2}+\frac{1}{2}+\frac{2}{x-1}\)
Theo AM-GM ta có : \(\frac{x-1}{2}+\frac{1}{2}+\frac{2}{x-1}\ge2\sqrt{\frac{x-1}{2}\cdot\frac{2}{x-1}}+\frac{1}{2}=2+\frac{1}{2}=\frac{5}{2}\)
Đẳng thức xảy ra <=> \(\frac{x-1}{2}=\frac{2}{x-1}\)
<=> ( x - 1 )2 = 4
<=> ( x - 1 )2 - 22 = 0
<=> ( x - 3 )( x + 1 ) = 0
<=> x = 3 ( tm ) hoặc x = -1 ( ktm )
=> x = 3
Vậy Min(y) = 5/2, đạt được khi x = 3