 giúp em vớii aa
giúp em vớii aa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


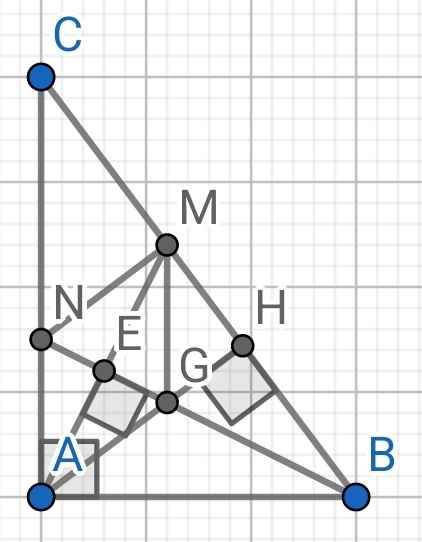
a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:
BA = BM (gt)
BE là cạnh chung
⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)
b) Do ∆ABE = ∆MBE (cmt)
⇒ ∠ABE = ∠MBE (hai góc tương ứng)
⇒ ∠ABN = ∠MBN
Xét ∆ABN và ∆MBN có:
BA = BM (gt)
∠ABN = ∠MBN (cmt)
BN là cạnh chung
⇒ ∆ABN = ∆MBN (c-g-c)
⇒ AN = MN (hai cạnh tương ứng)
c) Do ∆ABN = ∆MBN (cmt)
⇒ ∠BAN = ∠BMN (hai góc tương ứng)
Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ∠BMN = 90⁰
⇒ MN ⊥ BM
⇒ MN ⊥ BC
Lại có AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
Mà MN ⊥ BC (cmt)
⇒ AH // MN
⇒ ∠MGN = ∠ANG (so le trong)

a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-50^0}{2}=65^0\)
Xét ΔABC có \(\widehat{ACB}>\widehat{BAC}\)
mà AB,BC lần lượt là cạnh đối diện của các góc ACB,BAC
nên AB>BC
b: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
c: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
nên EF//BC

a) Ta có:
x² ≥ 0 với mọi x ∈ R
⇒ x² + 4 > 0 với mọi x ∈ R
Vậy đa thức đã cho không có nghiệm
b) Ta có:
⇒ (x - 1)² ≥ 0 với mọi x ∈ R
≺ (x - 1)² + 7 > 0 với mọi x ∈ R
Vậy đa thức đã cho không có nghiệm
c) x² + 2x + 2
= x² + x + x + 1 + 1
= (x² + x) + (x + 1) + 1
= x(x + 1) + (x + 1) + 1
= (x + 1)(x + 1) + 1
= (x + 1)² + 1
Ta có:
(x + 1)² ≥ 0 với mọi x ∈ R
⇒ (x + 1)² + 1 > 0 với mọi x ∈ R
Vậy đa thức đã cho không có nghiệm


a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:
BA = BM (gt)
BE là cạnh chung
⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)
b) Do ∆ABE = ∆MBE (cmt)
⇒ ∠ABE = ∠MBE (hai góc tương ứng)
⇒ ∠ABN = ∠MBN
Xét ∆ABN và ∆MBN có:
BA = BM (gt)
∠ABN = ∠MBN (cmt)
BN là cạnh chung
⇒ ∆ABN = ∆MBN (c-g-c)
⇒ AN = MN (hai cạnh tương ứng)
c) Do ∆ABN = ∆MBN (cmt)
⇒ ∠BAN = ∠BMN (hai góc tương ứng)
Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ∠BMN = 90⁰
⇒ MN ⊥ BM
⇒ MN ⊥ BC
Lại có AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
Mà MN ⊥ BC (cmt)
⇒ AH // MN
⇒ ∠MGN = ∠ANG (so le trong)
Cho tam giác ABC vuông tại A ( AB < AC ). Trên tia đối của tia AB, lấy điểm D sao cho AB = AD
a) Chứng minh tam giác ACB = tam giác ACD từ đó suy ra tam giác BCD cân.
b) Gọi E, F lần lượt là trung điểm của CD và BC, BE cắt CA tại I. Chứng minh, D, I, F thẳng hàng.
c) Kẻ đường thẳng qua D, song song BC và cắt BE tại M. Gọi G là giao điểm của MA và CD. Chứng minh BC = 6GF
Giúp tui câu này nha 🥺

Với n = 1 > 0, ta có:
2ⁿ + 2 = 4
2n + 5 = 7
Mà 4 < 7
⇒ 2ⁿ + 2 > 2n + 5 là vô lí
Em xem lại đề nhé

g: \(\left(3x^4-2x^3+x^2\right):\dfrac{1}{3}x^2\)
\(=\dfrac{3x^4}{\dfrac{1}{3}x^2}-\dfrac{2x^3}{\dfrac{1}{3}x^2}+\dfrac{x^2}{\dfrac{1}{3}x^2}\)
\(=9x^2-6x+3\)
h: \(\dfrac{x^3-3x^2+6x}{-3x}\)
\(=-\dfrac{x^3}{3x}+\dfrac{3x^2}{3x}-\dfrac{6x}{3x}\)
\(=-\dfrac{1}{3}x^2+x-2\)
i: \(\dfrac{2x^2-5x+3}{2x-3}\)
\(=\dfrac{2x^2-3x-2x+3}{2x-3}\)
\(=\dfrac{x\left(2x-3\right)-\left(2x-3\right)}{2x-3}=x-1\)
j: \(\dfrac{x^5+x+1}{x^3-x}\)
\(=\dfrac{x^5-x^3+x^3-x+2x+1}{x^3-x}\)
\(=\dfrac{x^2\left(x^3-x\right)+\left(x^3-x\right)+2x+1}{x^3-x}\)
\(=x^2+1+\dfrac{2x+1}{x^3-x}\)

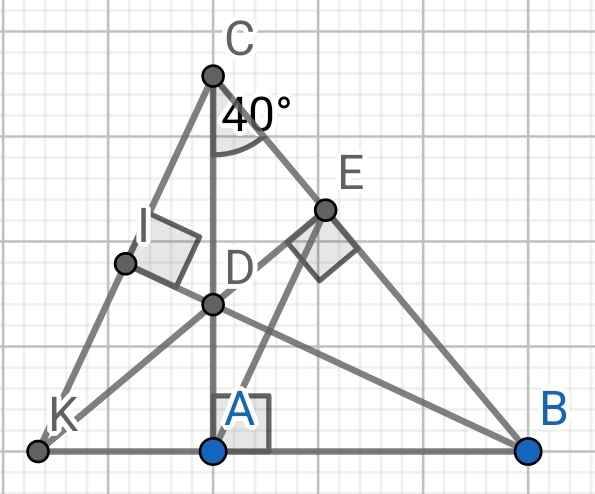
a) ∆ABC vuông tại A (gt)
⇒ ∠CBA + ∠ACB = 90⁰
⇒ ∠CBA = 90⁰ - ∠ACB
= 90⁰ - 40⁰
= 50⁰
b) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét hai tam giác vuông: ∆ABD và ∆EBD có:
BD là cạnh chung
∠ABD = ∠EBD (cmt)
⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)
c) Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
⇒ ∆ADE cân tại D
d) Do CI ⊥ BD (gt)
⇒ BI ⊥ CK
⇒ BI là đường cao của ∆BCK
Do ∆ABC vuông tại A (gt)
⇒ CA ⊥ AB
⇒ CA ⊥ BK
⇒ CA là đường cao thứ hai của ∆BCK
Mà CA và BI cắt nhau tại D
⇒ KD là đường cao thứ ba của ∆BCK
Mà DE ⊥ BC (gt)
⇒ K, D, E thẳng hàng

a) (2x³ - 3x² + x) + (x³ - x² + 2x + 1)
= 2x³ - 3x² + x + x³ - x² + 2x + 1
= (2x³ + x³) + (-3x² - x²) + (x + 2x) + 1
= 3x³ - 4x² + 3x + 1
b) (2x³ - 3x² + x) - (x³ - x² + 2x + 1)
= 2x³ - 3x² + x - x³ + x² - 2x - 1
= (2x³ - x³) + (-3x² + x²) + (x - 2x) - 1
= x³ - 2x² - x - 1
e) (2x + 1)(x³ - 4x + 5)
= 2x.(x³ - 4x + 5) + 1.(x³ - 4x + 5)
= 2x⁴ - 8x² + 10x + x³ - 4x + 5
= 2x⁴ + x³ - 8x² + (10x - 4x) + 5
= 2x⁴ + x³ - 8x² + 6x + 5
f) 3(x² - 2x)(3x + 1)
= (3x² - 6x)(3x + 1)
= 3x²(3x + 1) - 6x(3x + 1)
= 3x².3x + 3x².1 - 6x.3x - 6x.1
= 9x³ + 3x² - 18x² - 6x
= 9x³ + (3x² - 18x²) - 6x
= 9x³ - 15x² - 6x

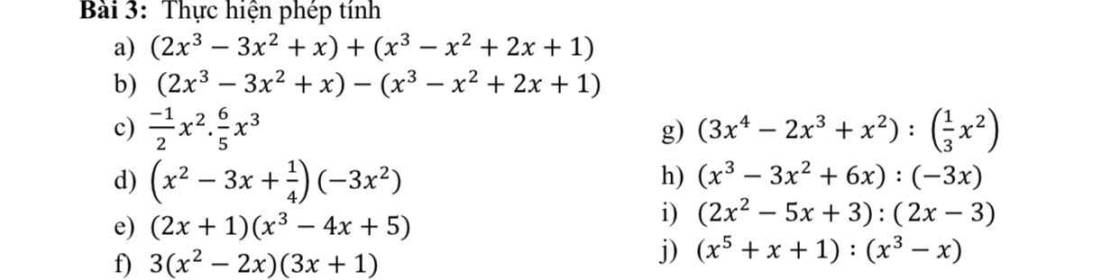

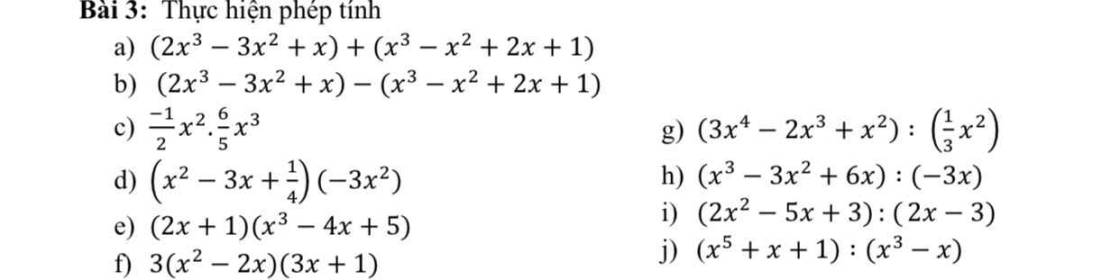
a: g=9x
nên g tỉ lệ thuận với x theo hệ số tỉ lệ là k=9
b: s*h=-130
=>s và h tỉ lệ nghịch với nhau theo hệ số tỉ lệ là k=-130