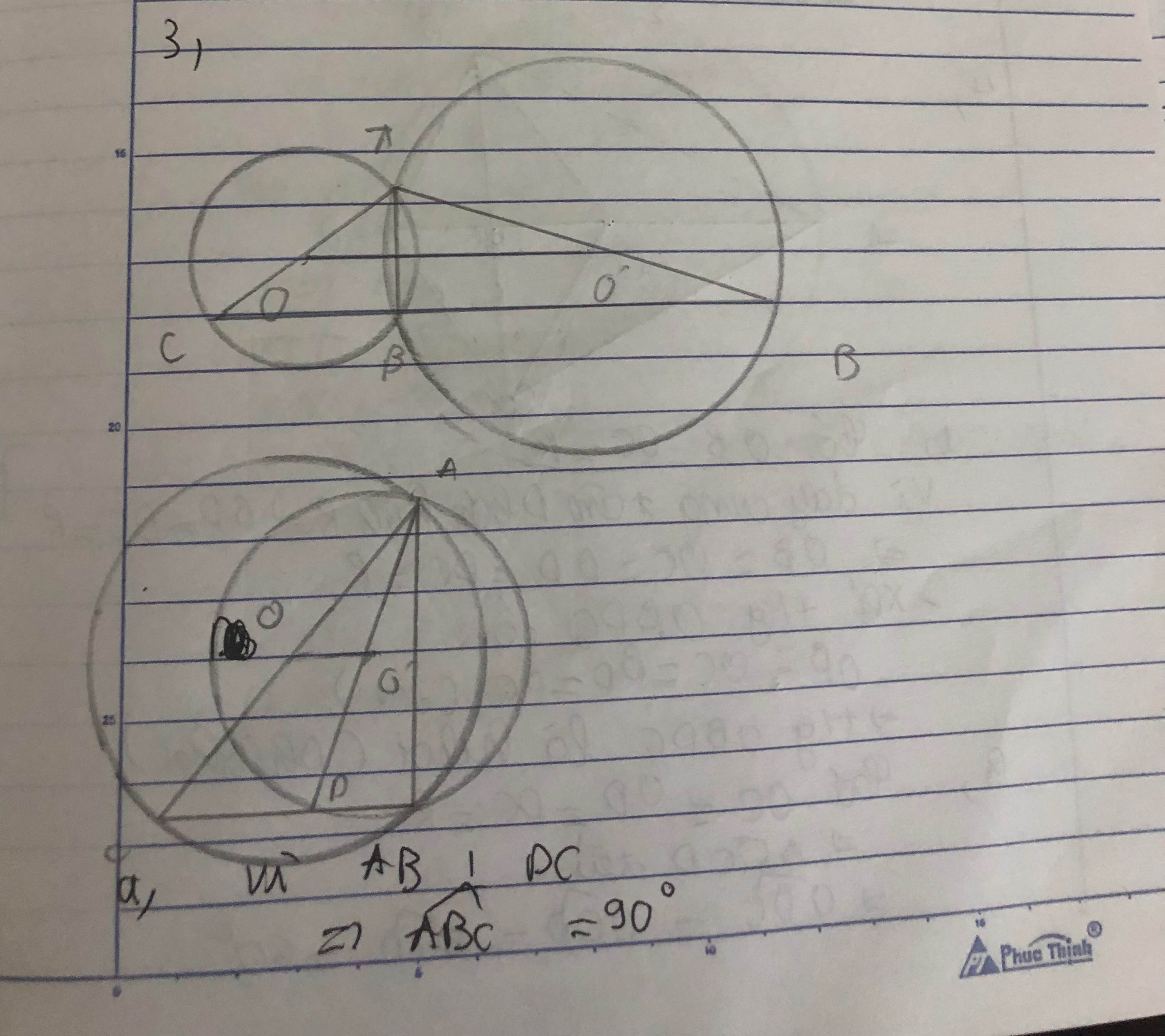
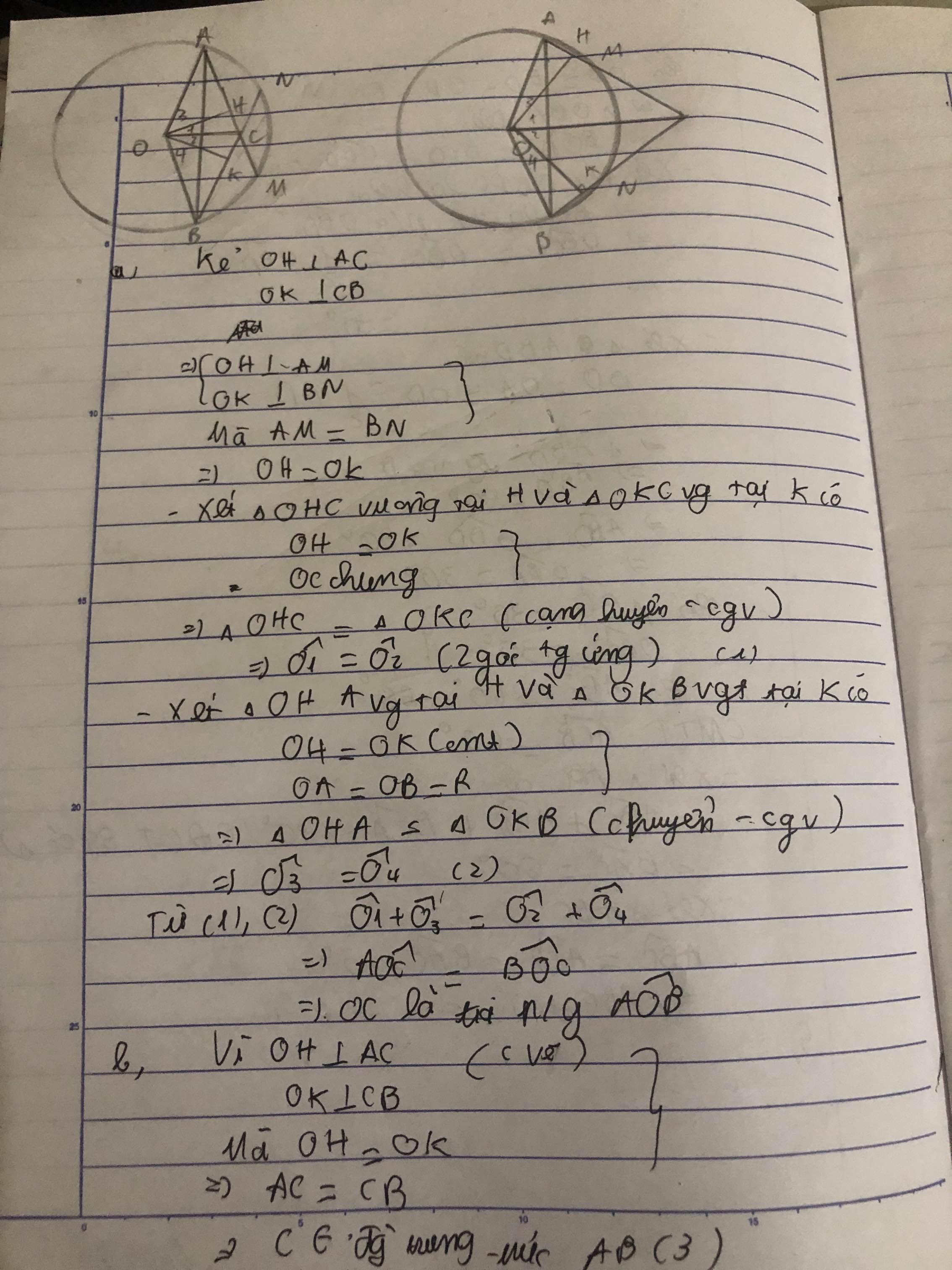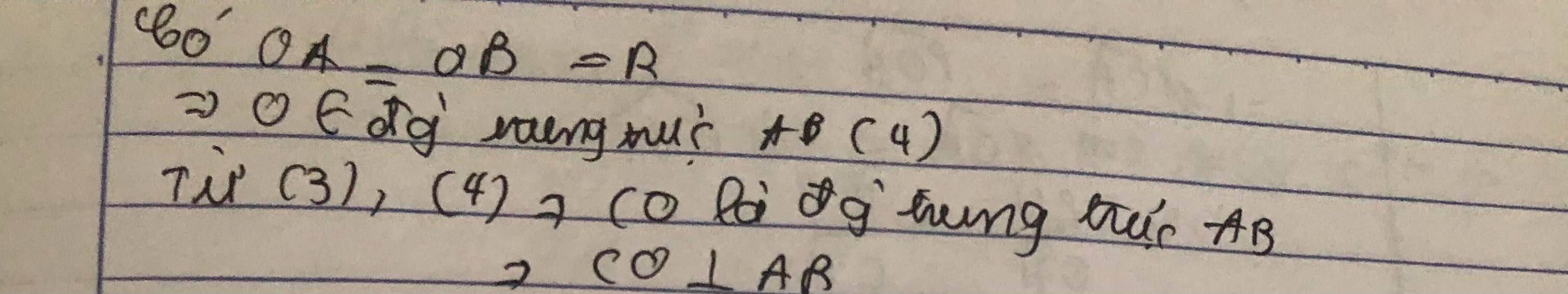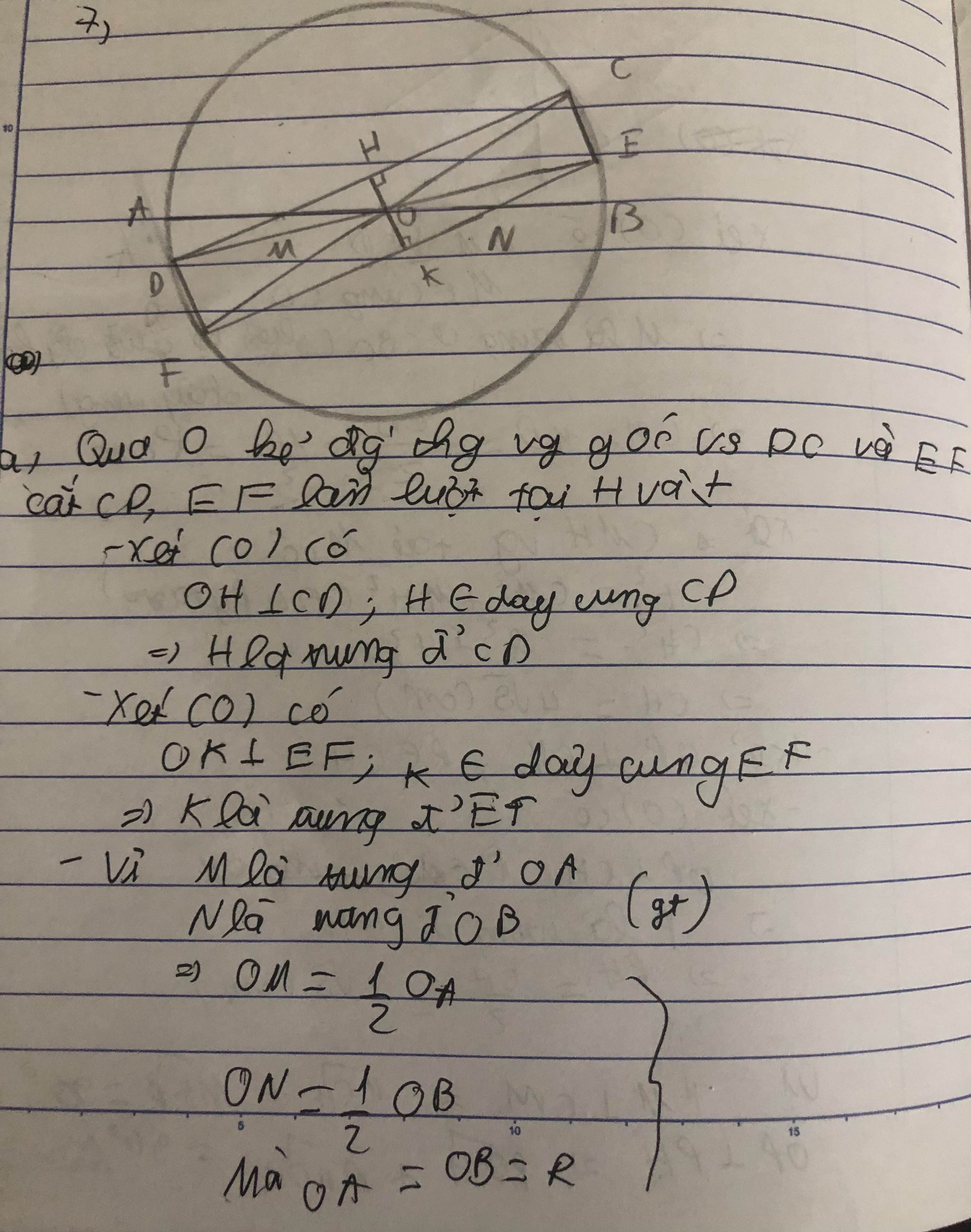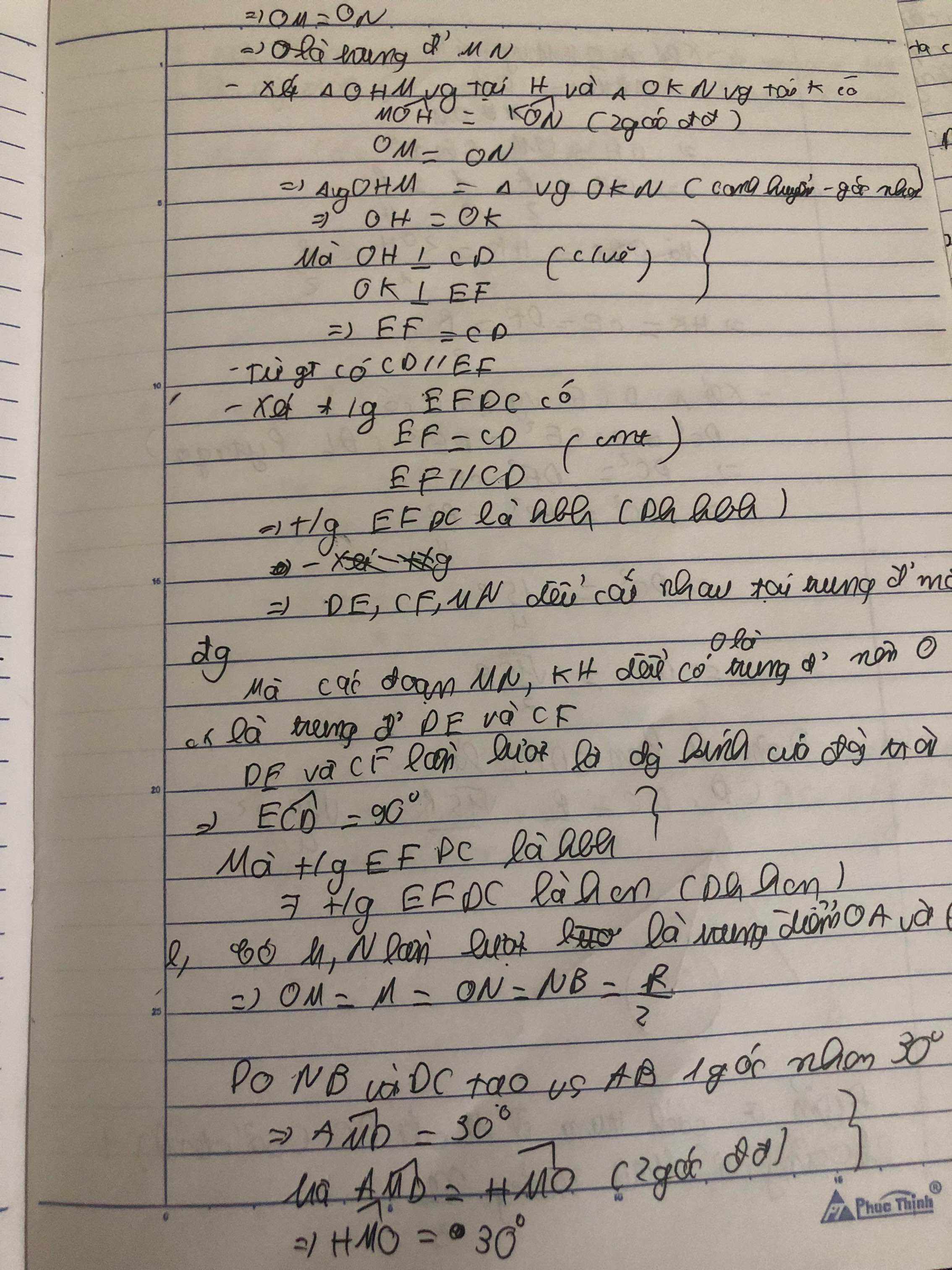Cho hai đường tròn $(O)$ và $(O')$ cắt nhau tại $A$ và $B$. Đường thẳng vuông góc với $AB$ tại B cắt các đường tròn $(O)$ và $(O')$ theo thứ tự tại $C$ và $D$ (khác $B$). Chứng minh rằng \(OO'=\frac{1}{2}CD\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Kẻ OP ⊥ AM, OQ ⊥ BN
Ta có: AM = BN (Giả thiết)
Suy ra: OP = OQ (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OCP và OCQ, ta có:
Góc OPC= góc OQC=90∘
OC chung
OP = OQ (chứng minh trên)
Suy ra: ∆OCP = ∆OCQ (cạnh huyền, cạnh góc vuông)
Góc O1= góc O2
Xét hai tam giác OAP và OBQ, ta có:
Góc OPA= góc OQB=90∘
OA = OB
OP = OQ ( chứng minh trên)
Suy ra: ∆OAP = ∆OBQ (cạnh huyền, cạnh góc vuông)
Góc O3= Góc O4
Suy ra: Góc O1+góc O3= Góc O2+ góc O4 hay Góc AOC= Góc BOC
Vậy OC là tia phân giác của Góc AOB
b) Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao ( tính chất tam giác cân).
Suy ra: OC ⊥ AB.

Ta có : \(\Delta=\left[-2\left(m+1\right)\right]^2-4\left(m^2+3\right)=\left(-2m-2\right)^2-4\left(m^2+3\right)\)
\(=\left(2m+2\right)^2-4\left(m^2+3\right)=4m^2+8m+4-4m^2-12=8m-8\)
Để phương trình có nghiệm \(8m-8>0\Leftrightarrow m< 1\)
\(8m-8=0\Leftrightarrow m=1\)
Theo Vi et ta có \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=\frac{2m+2}{1}=2m+2\\x_1x_1=\frac{c}{a}=m^2+3\end{cases}}\)
\(P=2m+2+m^2+3=m^2+2m+5\)
\(=m^2+2m+1+4=\left(m+1\right)^2+4\ge4\)
Dấu ''='' xảy ra <=> m = -1
Vậy GTNN P là 4 <=> m =-1
Để phương trình 1 có nghiệm \(=>\Delta\ge0\)
\(\Delta=4.\left(m+1\right)^2-4.\left(m^2+3\right)=4m^2+8m+4-4m^2-12=8m-8\ge0=>m\ge1\)

Cho phương trình x2 + ( m - 3 )x - 2m - 1 = 0 (1)
a) Với m = 1, thay vào (1) ta được pt : x2 - 2x - 3 = 0
Dễ thấy pt trên có a - b + c = 1 + 2 - 3 = 0
nên pt có hai nghiệm x1 = -1 ; x2 = -c/a = 3
Vậy với m = 1 thì pt có hai nghiệm x1 = -1 ; x2 = 3
b) Xét Δ ta có :
Δ = b2 - 4ac = ( m - 3 )2 - 4( -2m - 1 )
= m2 - 6m + 9 + 8m + 4
= m2 + 2m + 13
Dễ thấy Δ = m2 + 2m + 13 = ( m + 1 )2 + 12 ≥ 12 > 0 ∀ m
hay (1) luôn có hai nghiệm với mọi m (đpcm)
c) lỗi quá e k nhìn rõ đề
a, Thay m = 1 vào phương trình ta được :
\(x^2-2x-3=0\Leftrightarrow x^2-2x+1-4=0\)
\(\Leftrightarrow\left(x-1\right)^2-4=0\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=-1\end{cases}}\)
Vậy với m = 1 thì x = -1 ; x = 3
b, \(x^2+\left(m-3\right)x-2m-1=0\Leftrightarrow x^2+\left(m-3\right)x-\left(2m+1\right)=0\)
\(\Delta=\left(m-3\right)^2+4\left(2m+1\right)=m^2-6m+9+8m+4\)
\(=m^2+2m+13=m^2+2m+\frac{1}{4}+\frac{51}{4}\)
\(=\left(m+\frac{1}{2}\right)^2+\frac{51}{4}>0\forall m\)
Vậy phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị m

Theo Viet \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=-1\\x_1x_2=\frac{c}{a}=-7\end{cases}}\)
Ta có : \(C=x_1\left(x_2+1\right)+x_2\left(x_1+1\right)\)
\(=x_1x_2+x_1+x_1x_2+x_2=2x_1x_2+x_1+x_2\)
\(\Rightarrow C=-14-1=-15\)
んuリ イ không giải phương trình
Theo hệ thức Vietè ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}\\x_1x_2=\frac{c}{a}\end{cases}}\)
Khi đó : \(C=x_1\left(x_2+1\right)+x_2\left(x_1+1\right)=x_1x_2+x_1+x_1x_2+x_2\)
\(=2x_1x_2+\left(x_1+x_2\right)=\frac{2c}{a}-\frac{b}{a}=\frac{2c-b}{a}=\frac{-14-1}{1}=-15\)
Vậy ...

a) Thay m = -12 vào phương trình ta có
x2 + 5x – 14 = 0
<=> x2 + 7x - 2x - 14 = 0
<=> (x2 + 7x ) - (2x + 14) = 0
<=> x(x + 7) - 2(x + 7) = 0
<=> (x - 2)( x + 7) = 0
<=> x - 2 = 0 hoặc x + 7 = 0
<=> x = 2 hoặc x = -7
Vậy tập nghiệm của phương trình là S={-7 ; 2 }
Em chỉ iết làm câu này câu sau em xin lỗi!
a, Thay m =-12 vào phương trình trên ta được :
\(PT\Leftrightarrow x^2+5x-14=0\)
Ta có : \(\Delta=25-4\left(-14\right)=25+56=81>0\)
Vậy ta có 2 nghiệm phân biệt
\(x_1=\frac{-5-9}{2}=-7;x_2=\frac{-5+9}{2}=2\)
Vậy với m = -12 thì x = -7 ; 2
b, Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=\frac{-5}{2}\\x_1x_2=\frac{c}{a}=\frac{m-2}{2}\end{cases}}\)
Ta có : \(\frac{1}{x_1-1}+\frac{1}{x_2-1}=2\)ĐK : \(x_1\ne1;x_2\ne1\)
Gọi \(x_1=a;x_2=b\)( em đặt cho dễ viết thôi nhé )
\(\frac{1}{a-1}+\frac{1}{b-1}=2\)
\(\Leftrightarrow\frac{b-1+a-1}{\left(a-1\right)\left(b-1\right)}=\frac{2\left(a-1\right)\left(b-1\right)}{\left(a-1\right)\left(b-1\right)}\)
\(\Rightarrow a+b-2=2\left(ab-a-b+1\right)\)
\(\Leftrightarrow a+b-2=2\left[ab-\left(a+b\right)+1\right]\)
hay \(-\frac{5}{2}-2=2\left(\frac{m-2}{2}+\frac{5}{2}+1\right)\)
\(\Leftrightarrow\frac{-9}{2}=2\left(\frac{m+5}{2}\right)\Leftrightarrow\frac{-9}{2}=\frac{2m+10}{2}\)
\(\Rightarrow2m+10=-9\Leftrightarrow m=-\frac{19}{2}\)

1) Thay x=0;y=1 vào (d)=>m=2
Hoành độ giao điểm là nghiệm của phương trình:\(x^2=x+m-1\)
\(x^2-x-m+1=0\)2 điểm phân biệt => \(\Delta>0\)
\(\Delta>0=>1-4.\left(-m+1\right)=4m-3>0=>m>\frac{3}{4}\)
Áp dụng hệ thức Vi-ét:
\(x_1+x_2=1;x_1x_2=-m+1\)
\(4.\left(\frac{1}{x_1}+\frac{1}{x_2}\right)-x_1x_2+3=0=>4.\left(\frac{x_1+x_2}{x_1x_2}\right)-x_1x_2+3=0\)
\(\Rightarrow\frac{4}{-m+1}+m-1+3=0=>\frac{4}{-m+1}+m-2=0=>m^2-3m-2=0\)
Dùng công thức nghiệm được \(\Rightarrow x_1=\frac{3-\sqrt{17}}{2}\left(KTM\right);x_2=\frac{3+\sqrt{17}}{2}\left(TM\right)\)
Vậy...