
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Áp dụng định lý Viet:
$x_1+x_2=\frac{7}{2}$
$x_1x_2=\frac{-3}{2}$
Khi đó:
$B=x_1^2x_2+x_2^2x_1-3x_1x_2=x_1x_2(x_1+x_2)-3x_1x_2$
$=\frac{-3}{2}.\frac{7}{2}-3.\frac{-3}{2}=\frac{-3}{4}$
2.
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m+1)^2-3(2m-1)\geq 0$
$\Leftrightarrow m^2-4m+4\geq 0$
$\Leftrightarrow (m-2)^2\geq 0\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=\frac{2(m+1)}{3}$
$x_1x_2=\frac{2m-1}{3}$
Để PT có 2 nghiệm $x_1,x_2<2$ thì:
\(\left\{\begin{matrix}
x_1+x_2< 4\\
(x_1-2)(x_2-2)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x_1+x_2<4\\
x_1x_2-2(x_1+x_2)+4>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{2(m+1)}{3}<4\\ \frac{2m-1}{3}-2.\frac{2(m+1)}{3}+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m<5\\ m< \frac{7}{2}\end{matrix}\right.\Leftrightarrow m< \frac{7}{2}\)
Vậy..........

Lời giải:
Gọi chiều dài và chiều rộng của khu đất lần lượt là $a$ và $b$ (m)
Theo bài ra ta có:
$ab=96$
$(a-1)(b+2)=ab+14$
$\Leftrightarrow ab+2a-b-2=ab+14$
$\Leftrightarrow 2a-b=16$
$\Leftrightarrow b=2a-16$. Thay vào điều kiện $ab=96$ suy ra:
$a(2a-16)=96$
$\Leftrightarrow a(a-8)=48$
$\Leftrightarrow a^2-8a-48=0$
$\Leftrightarrow (a+4)(a-12)=0$
Do $a>0$ nên $a=12$
$b=96:12=8$
Vậy chiều dài và chiều rộng khu đất lần lượt là $12$ m và $8$ m
Gọi chiều rộng và chiều dài khu đất lần lượt là a(m),b(m)
(Điều kiện: a>0; b>0)
Nếu tăng chiều rộng thêm 2m và giảm chiều dài đi 1m thì diện tích tăng thêm 14m2 nên ta có:
(a+2)(b-1)=ab+14
=>ab-a+2b-2=ab+14
=>-a+2b=16
=>a-2b=-16
=>a=2b-16
Diện tích là 96m2 nên ab=96
=>\(b\left(2b-16\right)=96\)
=>\(b\left(b-8\right)=48\)
=>\(b^2-8b-48=0\)
=>(b-12)(b+4)=0
=>\(\left[{}\begin{matrix}b=12\left(nhận\right)\\b=-4\left(loại\right)\end{matrix}\right.\)
Vậy: Chiều dài là 12m; Chiều rộng là 96:12=8(m)

a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>CD\(\perp\)AB tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)AC tại E
Xét ΔABC có
BE,CD là các đường cao
BE cắt CD tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
Xét tứ giác HECF có \(\widehat{HEC}+\widehat{HFC}=90^0+90^0=180^0\)
nên HECF là tứ giác nội tiếp
=>\(\widehat{HEF}=\widehat{HCF}\)
b: Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)
nên ADHE là tứ giác nội tiếp
=>\(\widehat{DEH}=\widehat{DAH}\)
mà \(\widehat{HEF}=\widehat{HCF}\)
và \(\widehat{DAH}=\widehat{HCF}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{DEB}=\widehat{FEB}\)
=>EB là phân giác của góc DEF

a: Để hàm số y=(m-2)x+m+3 đồng biến thì m-2>0
=>m>2
b: Để đồ thị hàm số y=(m-2)x+m+3 song song với đường thẳng y=2x+7 thì
\(\left\{{}\begin{matrix}m-2=2\\m+3\ne7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=4\\m\ne4\end{matrix}\right.\)
=>\(m\in\varnothing\)
Hàm số y = (m + 2)x + 3 là hàm số bậc nhất khi m + 2 ≠ 0, hay m ≠ – 2.
Vậy ta có điều kiện m ≠ – 2.
a) Đồ thị hàm số đã cho song song với đường thẳng y = –x khi m + 2 = –1, tức là m = –3.
Giá trị này thỏa mãn điều kiện m ≠ – 2.
Vậy giá trị m cần tìm là m = –3.
b) Với m = –3 ta có hàm số y = –x + 3.
Đồ thị hàm số y = –x + 3 là đường thẳng đi qua hai điểm (0; 3) và (3; 0).


\(\left\{{}\begin{matrix}8x-y=6\\x^2-y=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-y-x^2+y=6+6\\8x-y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2-8x=-12\\y=8x-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2-8x+12=0\\y=8x-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x-2\right)\left(x-6\right)=0\\y=8x-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{2;6\right\}\\y=8x-6\end{matrix}\right.\)
Khi x=2 thì \(y=8\cdot2-6=16-6=10\)
Khi x=6 thì \(y=8\cdot6-6=42\)
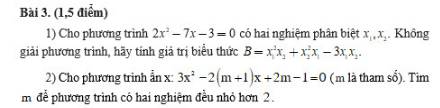

Lời giải:
a.
Vì $MC, MD$ là tiếp tuyến của $(O)$ nên $MC\perp OC, MD\perp OD$
$\Rightarrow \widehat{MCO}=\widehat{MDO}=90^0$
Tứ giác $MCOD$ có tổng 2 góc đối nhau $\widehat{MCO}+\widehat{MDO}=90^0+90^0=180^0$ nên $MCOD$ là tứ giác nội tiếp.
$\Rightarrow M,C,O,D$ cùng thuộc 1 đường tròn (1)
Mặt khác:
$K$ là trung điểm $AB$ nên $OK\perp AB$.
$\Rightarrow \widehat{MKO}=90^0$
Tứ giác $MCKO$ có $\widehat{MCO}=\widehat{MKO}=90^0$ và cùng nhìn cạnh $MO$ nên $MCKO$ là tứ giác nội tiếp.
$\Rightarrow M,C,K,O$ cùng thuộc 1 đường tròn (2)
Từ $(1); (2)\Rightarrow M,C,K,O,D$ cùng thuộc 1 đường tròn.
$\Rightarrow MCKD$ là tứ giác nội tiếp.
b.
Xét tam giác $MCA$ và $MBC$ có:
$\widehat{M}$ chung
$\widehat{MCA}=\widehat{MBC}$ (góc tạo bởi tt và dây cung bằng góc nt chắn cung đó)
$\Rightarrow \triangle MCA\sim \triangle MBC$ (g.g)
$\Rightarrow \frac{MC}{MA}=\frac{MB}{MC}\Rightarrow MC^2=MA.MB(3)$
Mặt khác:
Xét tam giác $MCN$ và $MKC$ có:
$\widehat{M}$ chung
$\widehat{MCN}=\widehat{MCD}=\frac{1}{2}\text{sđc(CD)}=\frac{1}{2}\widehat{COD}=\widehat{COM}=\widehat{MKC}$ (do $MCKO$ là tgnt)
$\Rightarrow \triangle MCN\sim \triangle MKC$ (g.g)
$\Rightarrow \frac{MC}{MK}=\frac{MN}{MC}$
$\Rightarrow MC^2=MK.MN(4)$
Từ $(3); (4)\Rightarrow MA.MB=MK.MN$
Hình vẽ: