3x=7y và x-y=-16 tính x và y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì \(\hept{\begin{cases}\widehat{A}+\widehat{B}=50^o+30^o=180^o\\\widehat{C}+\widehat{B}=40^o+140^o=180^o\end{cases}}\)mà \(\hept{\begin{cases}\widehat{A}\text{ và }\widehat{B}\text{ là 2 góc trong cùng phía}\\\widehat{C}\text{ và }\widehat{B}\text{ là 2 góc trong cùng phía}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}AD//BE\\CD//BE\end{cases}}\Rightarrow AD//CD\)

Ta có :
\(\left(6-x\right).\left(x-\frac{1}{3}\right)< 0\)
\(\Rightarrow6-x\text{ và }x-\frac{1}{3}\)trái dấu
+) Xét \(6-x< x-\frac{1}{3}\)
\(\Rightarrow\hept{\begin{cases}6-x< 0\\x-\frac{1}{3}>0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x>6\\x>\frac{1}{3}\end{cases}}\Leftrightarrow x>6\)
+) Xét \(6-x>x-\frac{1}{3}\)
\(\Rightarrow\hept{\begin{cases}6-x>0\\x-\frac{1}{3}< 0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x< 6\\x< \frac{1}{3}\end{cases}}\Leftrightarrow x< \frac{1}{3}\)

m // n thì M1 + N1 = 180 độ
mà M1 - N1 = 50 độ
=> M1 = 115 độ, N1 = 65 độ
=> M2 = 65 độ, N2 = 115 độ
Toán hình còn tùy vào cách trình bày của giáo viên nữa nhé, đây là làm hơi tắt
Ta có M 1 ^ − N 1 ^ = 50 ° (đề bài) (1)
Lại có n // m nên M 1 ^ + N 1 ^ = 180 ° (2) (hai góc trong cùng phía)
Từ (1) và (2) ⇒ 2 M 1 ^ = 230 ° ⇒ M 1 ^ = 115 ° .
Từ (1) có N 1 ^ = 115 ° − 50 ° = 65 ° .
Do n // m nên : N 2 ^ = M 1 ^ = 115 ° (hai góc so le trong).
N 1 ^ = M 2 ^ = 65 ° (hai góc so le trong)

Tổng các hệ số của đa thức đã cho sau khi khai triển là:
\(A\left(1\right)=\left(3-4.1+1^2\right)^{2004}.\left(3+4.1+1^2\right)^{2005}=0\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\Leftrightarrow a=b=c\).
Khi đó \(\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}=\frac{2a}{a}+\frac{2a}{a}+\frac{2a}{a}=2+2+2=6\).
Chọn C.

Bài 1 :
a) \(-\frac{3}{4}.31\frac{11}{23}-0,75.8\frac{12}{23}\)
\(=\left(-1\right).\frac{3}{4}.31\frac{11}{23}-\frac{3}{4}.8\frac{12}{23}\)
\(=\frac{3}{4}.\left[\left(-1\right).31\frac{11}{23}-8\frac{12}{23}\right]\)
\(=\frac{3}{4}.\left(-31\frac{11}{23}-8\frac{12}{23}\right)\)
\(=\frac{3}{4}.\left(-40\right)=-30\)
b) \(4\frac{5}{9}:\left(-\frac{5}{7}\right)+5\frac{4}{9}:\left(-\frac{5}{7}\right)\)
\(=4\frac{5}{9}.\frac{7}{5}+5\frac{4}{9}.\frac{7}{5}\)
\(=\left(4\frac{5}{9}+5\frac{4}{9}\right).\frac{7}{5}\)
\(=10.\frac{7}{5}=14\)
c) \(\left(\frac{12}{35}-\frac{6}{7}+\frac{18}{14}\right):\frac{6}{-7}-\frac{-2}{5}-\left(-2021\right)^0\)
\(=\left(\frac{12}{35}-\frac{30}{35}+\frac{45}{35}\right):\frac{6}{-7}+\frac{2}{5}-1\)
\(=27.\frac{-7}{6}-\frac{3}{5}\)
\(=\frac{-321}{10}\)
Bài 2 :
a) \(\left(2x-3\right)\left(\frac{3}{4}x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x-3=0\\\frac{3}{4}x+1=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}2x=3\\\frac{3}{4}x=-1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{3}{2}\\x=\frac{-4}{3}\end{cases}}\)
b) \(\frac{2}{3}x+\left(\frac{5}{7}\right)^0=\frac{3}{10}\)
\(\Rightarrow\frac{2}{3}x+1=\frac{3}{10}\)
\(\Rightarrow\frac{2}{3}x=\frac{-7}{10}\)
\(\Rightarrow x=\frac{-7}{10}:\frac{2}{3}=\frac{-21}{20}\)
c) \(\frac{3}{7}+\frac{1}{7}:x=\frac{3}{14}\)
\(\Rightarrow\frac{1}{7}:x=\frac{3}{14}-\frac{3}{7}=\frac{-3}{14}\)
\(\Rightarrow x=\frac{1}{7}:\frac{-3}{14}=\frac{-2}{3}\)
d) \(\frac{x+5}{2005}+\frac{x+6}{2004}+\frac{x+7}{2003}=-3\)
\(\Rightarrow\left(\frac{x+5}{2005}+1\right)+\left(\frac{x+6}{2004}+1\right)+\left(\frac{x+7}{2003}+1\right)=-3+1+1+1\)
\(\Rightarrow\frac{x+2010}{2005}+\frac{x+2010}{2004}+\frac{x+2010}{2003}=0\)
\(\Rightarrow\left(x+2010\right).\left(\frac{1}{2005}+\frac{1}{2004}+\frac{1}{2003}\right)=0\)
\(\Rightarrow x+2010=0\left(\text{ do }\frac{1}{2005}+\frac{1}{2004}+\frac{1}{2003}\ne0\right)\)
=> x = -2010

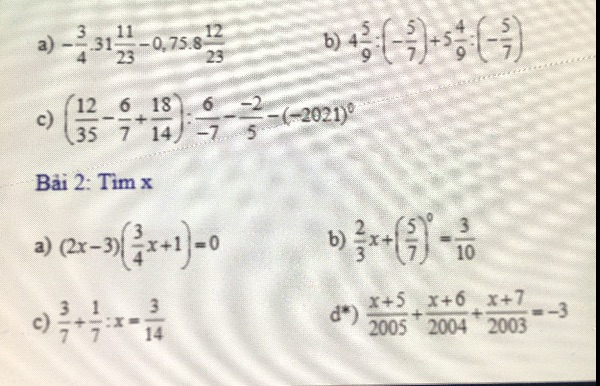
Ta có :
x - y = -16
3x = 7y
\(\Rightarrow\frac{x}{7}=\frac{y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\Rightarrow\frac{x}{7}=\frac{y}{3}=\frac{x-y}{7-3}=\frac{-16}{4}=-4\)
\(\Rightarrow\hept{\begin{cases}x=-4.7=-28\\y=-4.3=-12\end{cases}}\)