Cho tam giác ABC nội tiếp đường tròn (O). Một đường tròn tiếp xúc với AB, AC lần lượt tại E, F và tiếp xúc trong với (O) tại S. SF cắt (O) tại K khác S. BK cắt EF tại I. a) C/m KA=KC. b) C/m KA²=KF×KS. c) C/m I là tâm đg tròn nt tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(B=(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{120})+(\frac{1}{121}+...+\frac{1}{140})+(\frac{1}{141}+....+\frac{1}{160})+(\frac{1}{161}+...+\frac{1}{180})+(\frac{1}{181}+...+\frac{1}{200})\)
\(> \frac{20}{120}+\frac{20}{140}+\frac{20}{160}+\frac{20}{180}+\frac{20}{200}=\frac{1627}{2520}> \frac{5}{8}\)

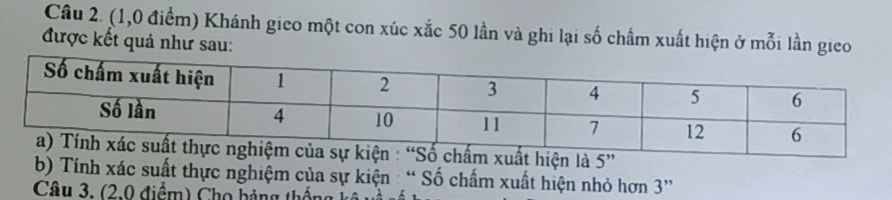
a: Gọi A là biến cố "Số chấm xuất hiện là 5"
=>n(A)=12
=>Xác suất thực nghiệm là \(P_A=\dfrac{12}{50}=0,24\)
b: Gọi B là biến cố "Số chấm xuất hiện nhỏ hơn 3"
=>n(B)=4+10=14
=>Xác suất thực nghiệm là \(P_B=\dfrac{14}{50}=0,28\)

Giả sử dây AB qua C \(\Rightarrow AB\le2R=20\)
Trong trường hợp \(AB\perp OC\), áp dụng định lý Pitago:
\(AB=2AC=2\sqrt{R^2-OC^2}=2\sqrt{19}\)
\(\Rightarrow2\sqrt{19}\le AB\le20\)
\(\Rightarrow AB=\left\{9;10;...;20\right\}\) có 12 dây có độ dài là số nguyên

a: Tổng vận tốc của hai xe là 54+36=90(km/h)
Hai xe gặp nhau sau khi đi được:
144:90=1,6(giờ)
b: Chỗ gặp cách B:
1,6x36=57,6(km)

Không đổi đơn vị độ dài (dm) sang đơn vị diện tích \(\left(m^2\right)\) được em nhé

NC=AN
=>N là trung điểm của AC
Xét ΔABC có
BN,CM là các đường trung tuyến
BN cắt CM tại O
Do đó: O là trọng tâm của ΔBAC
=>\(BO=\dfrac{2}{3}BN\)
=>\(S_{OMB}=\dfrac{2}{3}\times S_{MBN}\)
=>\(S_{MBN}=S_{OMB}:\dfrac{2}{3}=6\left(cm^2\right)\)
Vì M là trung điểm của AB
nên \(AB=2\times BM\)
=>\(S_{ANB}=2\times S_{MBN}=12\left(cm^2\right)\)
Vì N là trung điểm của AC
nên AC=2xAN
=>\(S_{ACB}=2\times S_{ABN}=24\left(cm^2\right)\)