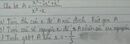
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 1.a. điều kiện xác định của phân thức là \(x^3-8\ne0\Leftrightarrow x\ne2\)
b .ta có \(\frac{3x^2+6x+12}{x^3-8}=\frac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\frac{3}{x+2}\)
bài 2.
\(A=\left(\frac{1}{x-1}-\frac{x}{1-x^3}.\frac{x^2+x+1}{x+1}\right):\frac{2x+1}{x^2+2x+1}\)
\(A=\left(\frac{1}{x-1}-\frac{x}{\left(1-x\right)\left(x^2+x+1\right)}.\frac{x^2+x+1}{x+1}\right).\frac{\left(x+1\right)^2}{2x+1}\)
\(A=\left(\frac{1}{x-1}-\frac{x}{\left(1-x\right)\left(x+1\right)}\right).\frac{\left(x+1\right)^2}{2x+1}\)
\(\Leftrightarrow A=\left(\frac{x+1+x}{\left(x-1\right)\left(x+1\right)}\right).\frac{\left(x+1\right)^2}{2x+1}=\frac{x+1}{x-1}\)
khi \(x=\frac{1}{2}\Rightarrow A=\frac{\frac{1}{2}+1}{\frac{1}{2}-1}=-3\)

bài 1.
a.\(\left(x+4\right)\left(x^2-4x+16\right)=x^3-4^3=x^3-64\)
b.\(\left(x^2-\frac{1}{3}\right)\left(x^4+\frac{1}{3}x^2+\frac{1}{9}\right)=\left(x^2\right)^3-\left(\frac{1}{3}\right)^3=x^6-\frac{1}{27}\)
bài 2.
a.\(892^2+892.216+108^2=892^2+2.892.108+108^2\)
\(=\left(892+108\right)^2=1000^2=1_{ }000_{ }000\)
b.\(36^2+26^2-52.36=36^2+26^2-2.26.36=\left(36-26\right)^2=10^2=100\)

Tương tự mấy phần kia
\(A=\frac{x+3}{x-2}+\frac{x+2}{3-x}+\frac{x+2}{x^2-5x+6}\)
\(=\frac{x+3}{x-2}-\frac{x+2}{x-3}+\frac{x+2}{\left(x-2\right)\left(x-3\right)}\)
\(=\frac{\left(x+3\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}-\frac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}+\frac{x+2}{\left(x-2\right)\left(x-3\right)}\)
\(=\frac{x^2-9-x^2+4+x+2}{\left(x-2\right)\left(x-3\right)}=\frac{-3+x}{\left(x-2\right)\left(x-3\right)}=\frac{-1}{x-2}\)

\(\frac{1}{x-2}-\frac{1}{x+2}+\frac{4x-x^2}{4-x^2}\)
\(=\frac{x+2}{\left(x-2\right)\left(x+2\right)}-\frac{x-2}{\left(x+2\right)\left(x-2\right)}+\frac{4x-x^2}{\left(2-x\right)\left(x+2\right)}\)
\(=\frac{x+2-x+2-4x+x^2}{\left(x+2\right)\left(x-2\right)}=\frac{-4x+4+x^2}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)}=\frac{x-2}{x+2}\)
\(\frac{1}{x-2}-\frac{1}{x+2}+\frac{4x-x^2}{4-x^2}\)
\(=\frac{1}{x-2}-\frac{1}{x+2}+\frac{x^2-4x}{x^2-4}\)
\(=\frac{1}{x-2}-\frac{1}{x+2}+\frac{x^2-4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x+2}{\left(x-2\right)\left(x+2\right)}-\frac{x-2}{\left(x-2\right)\left(x+2\right)}+\frac{x^2-4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x+2-x+2+x^2-4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x^2-4x+4}{\left(x-2\right)\left(x+2\right)}=\frac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\frac{x-2}{x+2}\)

\(\frac{2x^2-1}{x^2-xy}+\frac{1-2y^2}{x^2-xy}=\frac{2x^2-1+1-2y^2}{x^2-xy}\)
\(=\frac{2x^2-2y^2}{x^2-xy}=\frac{2\left(x^2-y^2\right)}{x\left(x-y\right)}\)
\(=\frac{2\left(x-y\right)\left(x+y\right)}{x\left(x-y\right)}=\frac{2\left(x+y\right)}{x}\)
Sửa đề : \(\frac{2x^2-1}{x^2-xy}+\frac{1-2y^2}{x^2-xy}\)
\(=\frac{2x^2-1+1-2y^2}{x^2-xy}=\frac{2x^2-2y^2}{x\left(x-y\right)}=\frac{2\left(x^2-y^2\right)}{x\left(x-y\right)}\)
\(=\frac{2\left(x-y\right)\left(x+y\right)}{x\left(x-y\right)}=\frac{2\left(x+y\right)}{x}\)

a, \(x^2-4x=0\Leftrightarrow x\left(x-4\right)=0\Leftrightarrow x=0;4\)
b, \(x^3+x^2-9x-9=0\Leftrightarrow x^2\left(x+1\right)-9\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-9\right)=0\Leftrightarrow\left(x+1\right)\left(x-3\right)\left(x+3\right)=0\Leftrightarrow x=-1;\pm3\)
c, \(x^2-3x-10=0\Leftrightarrow x^2+2x-5x-10=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+2\right)=0\Leftrightarrow x=5;-2\)

a, \(20x^2y^3-15xy^2=5xy^2\left(4xy-3\right)\)
b, \(3x+3y-x^2-xy=3\left(x+y\right)-x\left(x+y\right)=\left(3-x\right)\left(x+y\right)\)
c, \(9-x^2-y^2+2xy=9-\left(x^2+y^2-2xy\right)\)
\(=3^2-\left(x-y\right)^2=\left(3-x+y\right)\left(3+x-y\right)\)
20x2y3 - 15xy2 = 5xy2( 4xy - 3 )
3x + 3y - x2 - xy = ( 3x + 3y ) - ( x2 + xy ) = 3( x + y ) - x( x + y ) = ( x + y )( 3 - x )
9 - x2 - y2 + 2xy = 9 - ( x2 - 2xy + y2 ) = 32 - ( x - y )2 = ( 3 - x + y )( 3 + x - y )

a)\(A=\frac{x^3-2x^2+x}{x^3-x}=\frac{x\left(x^2-2x+1\right)}{x\left(x^2-1\right)}=\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\frac{x-1}{x+1}\)
ĐKXĐ : \(\hept{\begin{cases}x\ne0\\x\ne\pm1\end{cases}}\)
b) \(\frac{x-1}{x+1}=\frac{x+1-2}{x+1}=1-\frac{2}{x+1}\)
Để A đạt giá trị nguyên => \(\frac{2}{x+1}\)đạt giá trị nguyên
=> 2 ⋮ x + 1
=> x + 1 ∈ Ư(2) = { ±1 ; ±2 }
So với ĐKXĐ ta thấy x = 0 ; x = -2 ; x = -3 thỏa mãn
Vậy x ∈ { -3 ; -2 ; 0 } thì A đạt giá trị nguyên
c) Tại x = -1/3 ( tm ) => A = \(\frac{-\frac{1}{3}-1}{-\frac{1}{3}+1}=-2\)