giúp với ạ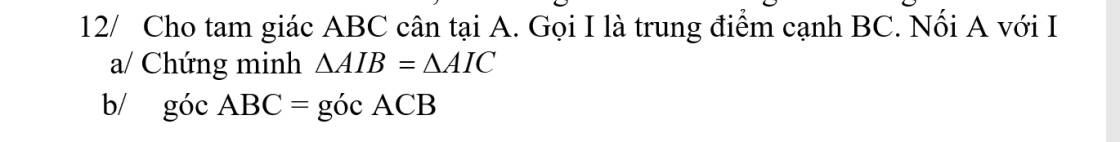
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: \(A\left(x\right)=2x^4+3x^2-x+3-x^2-x^4-6x^3\)
\(=\left(2x^4-x^4\right)-6x^3+\left(3x^2-x^2\right)-x+3\)
\(=x^4-6x^3+2x^2-x+3\)
\(B\left(x\right)=10x^3+3-x^4-4x^3+4x-2x^2\)
\(=-x^4+\left(10x^3-4x^3\right)-2x^2+4x+3\)
\(=-x^4+6x^3-2x^2+4x+3\)
b: M(x)=A(x)+B(x)
\(=x^4-6x^3+2x^2-x+3-x^4+6x^3-2x^2+4x+3\)
=3x+6
N(x)=A(x)-B(x)
\(=x^4-6x^3+2x^2-x+3+x^4-6x^3+2x^2-4x-3\)
\(=2x^4-12x^3+4x^2-5x\)
c: M(x)=0
=>3x+6=0
=>3x=-6
=>x=-2
Bài 3:
a: \(A\left(x\right)=x-5x^3-2x^2+9x^3-\left(x-1\right)-2x^2\)
\(=\left(-5x^3+9x^3\right)+\left(-2x^2-2x^2\right)+\left(x-x\right)+1\)
\(=4x^3-4x^2+1\)
\(B\left(x\right)=-4x^3-2\left(x^2+1\right)+6x+2x^2-9x+2x^3\)
\(=\left(-4x^3+2x^3\right)+\left(-2x^2+2x^2\right)+6x-9x-2\)
\(=-2x^3-3x-2\)
\(C\left(x\right)=2x-6x^2-4+x^3\)
\(=x^3-6x^2+2x-4\)
b: M(x)=A(x)+B(x)-C(x)
\(=4x^3-4x^2+1-2x^3-3x-2-x^3+6x^2-2x+4\)
\(=x^3+2x^2-5x+3\)
c: \(P\left(x\right)=3\cdot M\left(x\right)-3x^3-9\)
\(=3x^3+6x^2-15x+9-3x^3-9=6x^2-15x\)
Đặt P(x)=0
=>\(6x^2-15x=0\)
=>\(2x^2-5x=0\)
=>x(2x-5)=0
=>\(\left[{}\begin{matrix}x=0\\x=\dfrac{5}{2}\end{matrix}\right.\)

Câu 3:
a: Xét ΔACE vuông tại A và ΔKCE vuông tại K có
CE chung
\(\widehat{ACE}=\widehat{KCE}\)
Do đó: ΔACE=ΔKCE
=>CA=CK và EA=EK
Ta có: CA=CK
=>C nằm trên đường trung trực của AK(1)
Ta có: EA=EK
=>E nằm trên đường trung trực của AK(2)
Từ (1),(2) suy ra CE là đường trung trực của AK
=>CE\(\perp\)AK
b: Xét ΔABC vuông tại A có \(cosACB=\dfrac{AC}{BC}\)
=>\(\dfrac{AC}{BC}=cos60=\dfrac{1}{2}\)
=>BC=2AC
Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-60^0=30^0\)
CE là phân giác của góc ACB
=>\(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}=30^0\)
Xét ΔEBC có \(\widehat{EBC}=\widehat{ECB}\left(=30^0\right)\)
nên ΔEBC cân tại E
=>EB=EC
mà EC>AC(ΔEAC vuông tại A)
nên EB>AC
c: Gọi H là giao điểm của BD với CA
Xét ΔCHB có
CD,BA là các đường cao
CD cắt BA tại E
Do đó: E là trực tâm của ΔCHB
=>HE\(\perp\)CB
mà EK\(\perp\)CB
nên H,E,K thẳng hàng
=>CA,EK,BD đồng quy
Bài 4:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>BA=BE
b: Xét ΔABC có AB<AC
mà \(\widehat{ACB};\widehat{ABC}\) lần lượt là góc đối diện của các cạnh AB,AC
nên \(\widehat{ACB}< \widehat{ABC}\)
mà \(\widehat{ACB}=\widehat{AMD}\left(=90^0-\widehat{ABC}\right);\widehat{ABC}=\widehat{ADM}\left(=90^0-\widehat{BME}\right)\)
nên \(\widehat{AMD}< \widehat{ADM}< \widehat{DAM}\)
=>AD<AM<DM
c: Xét ΔDAM vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADM}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAM=ΔDEC
=>DM=DC
=>D nằm trên đường trung trực của MC(1)
ta có: BA+AM=BM
BE+EC=BC
mà BA=BE và AM=EC(ΔDAM=ΔDEC)
nên BM=BC
=>B nằm trên đường trung trực của MC(2)
Ta có: KM=KC
=>K nằm trên đường trung trực của MC(3)
từ (1),(2),(3) suy ra B,D,K thẳng hàng

a: \(f\left(x\right)⋮g\left(x\right)\)
=>\(2x^2-x+2⋮x+1\)
=>\(2x^2+2x-3x-3+5⋮x+1\)
=>\(5⋮x+1\)
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
b: \(f\left(x\right)⋮g\left(x\right)\)
=>\(3x^2-4x+6⋮3x-1\)
=>\(3x^2-x-3x+1+5⋮3x-1\)
=>\(5⋮3x-1\)
=>\(3x-1\in\left\{1;-1;5;-5\right\}\)
=>\(3x\in\left\{2;0;6;-4\right\}\)
=>\(x\in\left\{\dfrac{2}{3};0;2;-\dfrac{4}{3}\right\}\)
mà x nguyên
nên \(x\in\left\{0;2\right\}\)
c: \(f\left(x\right)⋮g\left(x\right)\)
=>\(-2x^3-7x^2-5x+5⋮x+2\)
=>\(-2x^3-4x^2-3x^2-6x+x+2+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)

Đặt A = (x² + 6)/(x² + 1)
Biểu thức đạt giá trị lớn nhất khi x² + 1 nhỏ nhất
Ta có:
x² ≥ 0 với mọi x ∈ R
⇒ x² + 1 ≥ 1 với mọi x ∈ R
⇒ x² + 1 nhỏ nhất là 1 khi x = 0
⇒ Giá trị lớn nhất của A là:
(0 + 6)/(0 + 1) = 6

Bổ sung đề: ΔABC vuông tại A
a: Xét ΔEAB và ΔEND có
EA=EN
\(\widehat{AEB}=\widehat{NED}\)(hai góc đối đỉnh)
EB=ED
Do đó: ΔEAB=ΔEND
=>\(\widehat{EAB}=\widehat{END}\)
=>AB//ND
b: Ta có: AB//ND
AB\(\perp\)AC
Do đó: ND\(\perp\)AC
Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên \(AD=\dfrac{BC}{2}=AB=BD\)
=>ΔABD đều
Ta có: ΔABD đều
mà AE là đường trung tuyến
nên AE\(\perp\)BD
Xét ΔANC có
CE,ND là các đường cao
CE cắt ND tại D
Do đó: D là trực tâm của ΔANC
=>AD\(\perp\)NC

\(Q\left(2\right)=3.2-6=0\)
\(P\left(-1\right)=4.\left(-1\right)+2=-2\)

a) *) P(x) có:
- Bậc 3.
- Hạng tử cao nhất: 1
- Hạng tử tự do: 1
*) Q(x) có:
- Bậc 4
- Hạng tử cao nhất: 1
- Hạng tử tự do: -1
b) P(x).A(x) = Q(x)
A(x) = Q(x) : P(x)
= (x⁴ - 1) : (x³ + x² + x + 1)
= (x² - 1)(x² + 1) : [(x³ + x²) + (x + 1)]
= (x - 1)(x + 1)(x² + 1) : [x²(x + 1) + (x + 1)]
= (x - 1)(x + 1)(x² + 1) : [(x + 1)(x² + 1)]
= (x - 1) . [(x + 1) : (x + 1)] . [(x² + 1) : (x² + 1)]
= x - 1

a: \(P\left(x\right)=9x^4+6x-3x^6+7\)
\(=-3x^6+9x^4+6x+7\)
bậc là 6
b: \(A\left(x\right)=-5x^6+3x-3x^2+5x^3+5x^6-1\)
\(=\left(-5x^6+5x^6\right)+5x^3-3x^2+3x-1\)
\(=5x^3-3x^2+3x-1\)
bậc là 3
c: \(B\left(x\right)=7x^3+5x^4-2x+x^2-3\)
\(=5x^4+7x^3+x^2-2x-3\)
Bậc là 4

a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
b: Xét ΔCFB và ΔCED có
CF=CE
\(\widehat{FCB}\) chung
CB=CD
Do đó: ΔCFB=ΔCED
=>BF=DE
c: ΔCFB=ΔCED
=>CB=CD
=>ΔCBD cân tại C
Ta có: ΔCBD cân tại C
mà CG là đường trung tuyến
nên CG là đường trung trực của BD(1)
Ta có: CF+FD=CD
CE+EB=CB
mà CF=CE và CD=CB
nên FD=EB
Xét ΔFDB và ΔEBD có
FD=EB
BD chung
FB=ED
Do đó: ΔFDB=ΔEBD
=>\(\widehat{IBD}=\widehat{IBD}\)
=>IB=ID
=>I nằm trên đường trung trực của BD(2)
Từ (1),(2) suy ra A,G,I thẳng hàng



a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
b: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)