Cho đa giác lồi \(H\) có diện tích \(S\) và chu vi \(P\). Chứng minh rằng ta có thể vẽ được một đường tròn bán kính \(R=\dfrac{S}{P}\) nằm hoàn toàn trong \(H\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xác suất để viên thứ nhất bắn trúng là 0,6 và viên thứ II trúng là 0,7
a.
Xác suất để cả 2 đều trượt: \(P\left(\overline{M}\right)=0,4.0,3=0,12\)
\(\Rightarrow\) Xác suất để có ít nhất 1 viên trúng: \(P\left(M\right)=1-0,12=0,88\)
b.
Có 2 trường hợp thỏa mãn: I trúng II trượt, I trượt II trúng
Xác suất: \(P\left(N\right)=0,6.0,3+0,4.0,7=0,46\)

Ta thấy \(a=1000^{1001}\)
\(=1000.1000^{1000}\)
\(=1000^{1000}+1000^{1000}+...+1000^{1000}\) (1000 lần)
\(>1^1+2^2+...+1000^{1000}\)
Nên \(a>c\)
Lại có \(2^{2^{64}}=2^{2^4.2^{60}}=\left(2^{2^4}\right)^{2^{60}}\) \(>\left(2^{10}\right)^{2^{10}}=1024^{1024}>1000^{1001}\) nên \(b>a\)
Vậy \(b>a>c\)


a.
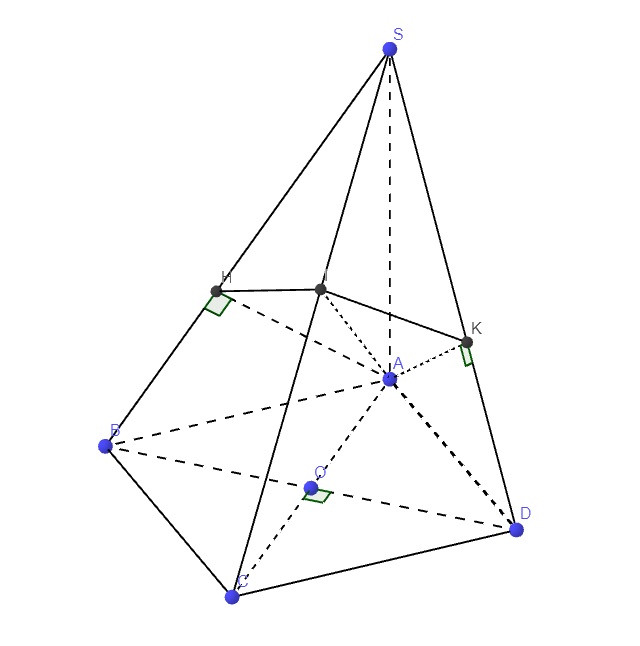
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{ hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow BD\perp\left(SAC\right)\)
Mà (SAC) đi qua trung điểm O của BD
\(\Rightarrow\left(SAC\right)\) là mp trung trực của BD
c.
Theo câu a ta có: \(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\\AH\in\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\left(gt\right)\)
\(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\)
Lại có \(AI\perp SC\left(gt\right)\)
\(\Rightarrow SC\perp\left(AIH\right)\) (1)
Tương tự, ta chứng minh được \(AK\perp\left(SCD\right)\Rightarrow AK\perp SC\)
\(\Rightarrow SC\perp\left(AIK\right)\) (2)
(1);(2) \(\Rightarrow\left(AIH\right)\) trùng \(\left(AIK\right)\) hay 3 đường AH, AI, AK cùng nằm trong 1 mp

chịu thôi anh ạ em mứi lớp 5 thôi ạ anh thông cảm nhé
ko thì anh lên google nhé
nhân tiện em chúc anh mừng năm mới vui vẻ nhé