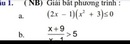
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: l = 1745,25m ± 0,01m có độ chính xác đến hàng phần trăm (độ chính xác là 0,01) nên ta quy tròn số đến hàng phần chục.
Vậy số quy tròn của 1745,25m là 1745,3 m.

Ta có: l = 1745,25m ± 0,01m có độ chính xác đến hàng phần trăm (độ chính xác là 0,01) nên ta quy tròn số đến hàng phần chục.
Vậy số quy tròn của 1745,25m là 1745,3 m.


để phương trình bậc 2 có hai nghiệm trái dấu thì điều kiện duy nhất là :
\(m^2-9< 0\Leftrightarrow-3< m< 3\Rightarrow m=\left\{-2,-1,0,1,2\right\}\)
nên tổng các phần tử của S=0 nên khoanh B

Vectro chỉ phương là (2,-1) nhé ( là phần hệ số của tham số t ấy bạn)

(a+b) + (b+c) - (c-a) = a+b+b+c-a+a = (a+a)+(b+b)+(c-c) = 2a+2b = 2.(a+b)

ĐK: \(x\ge-3\).
\(2\sqrt{x+3}=4x^3+3x-3\)
\(\Leftrightarrow2\left(\sqrt{x+3}-2\right)=4x^3+3x-7\)
\(\Leftrightarrow2\frac{x+3-4}{\sqrt{x+3}+2}=\left(x-1\right)\left(4x^2+4x+7\right)\)
\(\Leftrightarrow\frac{2\left(x=1\right)}{\sqrt{x+3}+2}=\left(x-1\right)\left(4x^2+4x+7\right)\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\left(1\right)\\\frac{2}{\sqrt{x+3}+2}=4x^2+4x+7\left(2\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow x=1\left(tm\right)\)
\(\left(2\right)\)có \(VT\le1,VP\ge6\)do đó vô nghiệm.

 giúp mình với ah
giúp mình với ah giúp mình với ja
giúp mình với ja
a. ta có \(x^2+3>0\text{ nên }\left(2x-1\right)\left(x^2+1\right)\le0\Leftrightarrow2x-1\le0\Leftrightarrow x\le\frac{1}{2}\)
b. ta có \(\frac{x+9}{x-1}>5\Leftrightarrow\frac{x+9-5x+5}{x-1}>0\Leftrightarrow\frac{14-4x}{x-1}>0\)
\(\hept{\begin{cases}14-4x>0\\x-1>0\end{cases}\Leftrightarrow\frac{7}{2}>x>1}\) hoặc \(\hept{\begin{cases}14-4x< 0\\x-1< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>\frac{7}{2}\\x< 1\end{cases}}}\) vô lí
vậy \(1< x< \frac{7}{2}\)
a) \(\left(2x-1\right)\left(x^2+3\right)\le0\)
\(\Leftrightarrow\hept{\begin{cases}2x-1\le0\\x^2+3\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}2x-1\ge0\\x^2+3\le0\end{cases}}\)
mà \(x^2+3>0\forall x\)
nên \(\hept{\begin{cases}2x-1\le0\\x^2+3>0\end{cases}}\)
\(\Leftrightarrow x\le\frac{1}{2}\)
Vậy nghiệm của BPT là \(x\le\frac{1}{2}\)
b) Đề bị che mất mẫu số nên không đọc được đề =))