Lời giải:

Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$

$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$

Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.

$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)

Mặt khác:

Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.

$\Rightarrow \widehat{MKO}=90^0$

Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.

$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)

Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.

Hình vẽ:

Lời giải:

Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$

$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$

Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.

$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)

Mặt khác:

Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.

$\Rightarrow \widehat{MKO}=90^0$

Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.

$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)

Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.

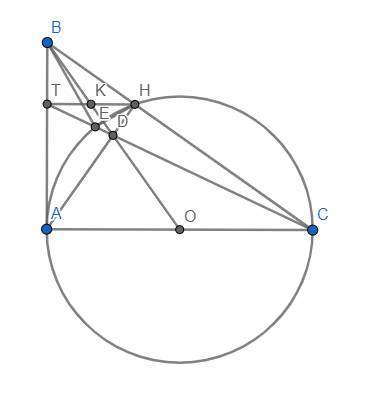
 Gọi T là giao điểm của CD và AB. Khi đó xét tứ giác ACHT, ta có:

O (trung điểm AC), D (giao điểm của 2 đường chéo) và B (giao điểm của 2 đường thẳng chứa 2 cạnh đối) thẳng hàng nên ACHT là hình thang. (bổ đề hình thang quen thuộc)

 \(\Rightarrow\) HT//AC \(\Rightarrow\) H, K, T thẳng hàng.

 Lại có \(\widehat{CEH}=\widehat{CAH}\) (góc nội tiếp cùng chắn cung AH)

 Mà \(\widehat{CAH}=\widehat{B}\) (cùng phụ với góc C)

 \(\Rightarrow\widehat{CEH}=\widehat{B}\)

 \(\Rightarrow\) Tứ giác BTEH nội tiếp \(\Rightarrow\widehat{BEH}=\widehat{BTH}\)

Mà \(\widehat{BTH}=90^o\) nên \(\widehat{BEH}=90^o\). Ta có đpcm.

A B C E O D H M N

a/

Xét tg ABD và tg ACE có

\(\widehat{BAC}\) chung

\(\widehat{ABD}=\widehat{ACE}\) (góc nội tiếp cùng chắn cung DE)

=> tg ABD đồng dạng với tg ACE (g.g.g)

\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\Rightarrow AD.AC=AE.AB\)

b/

\(\widehat{BEC}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow CE\perp AB\)

\(\widehat{BDC}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow BD\perp AC\)

=> H là trực tâm của tg ABC \(\Rightarrow AH\perp BC\) (trong tg 3 đường cao đồng quy)

a) Tứ giác BCDE nội tiếp nên \(\widehat{ABD}=\widehat{ACE}\). Từ đó dễ dàng chứng minh \(\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrow AD.AC=AB.AE\) (đpcm)

b) Đường tròn (O) có đường kính BC nên \(\widehat{BEC}=\widehat{BDC}=90^o\) (góc nội tiếp chắn nửa đường tròn)

 \(\Rightarrow BD\perp AC,CE\perp AB\) \(\Rightarrow\) H là trực tâm tam giác ABC

 \(\Rightarrow AH\perp BC\) (đpcm)

c) Hạ \(HS\perp AO\) tại S. \(\Rightarrow S\in\left(AH\right)\). Khi đó tứ giác OKHS nội tiếp nên \(AS.AO=AH.AK=AD.AC=AN^2\) .

 Từ đây dễ dàng chứng minh \(\Delta ASN~\Delta ANO\left(c.g.c\right)\) \(\Rightarrow\widehat{ASN}=\widehat{ANO}\). Ta có \(\widehat{ANO}=90^o\Rightarrow\widehat{ASN}=90^o\) hay \(SN\perp AO\) tại S

 Hoàn toàn tương tự, ta chứng minh được \(SM\perp AO\) tại S

 Lại có \(HS\perp AO\) tại S nên H, M, N thẳng hàng (đpcm).

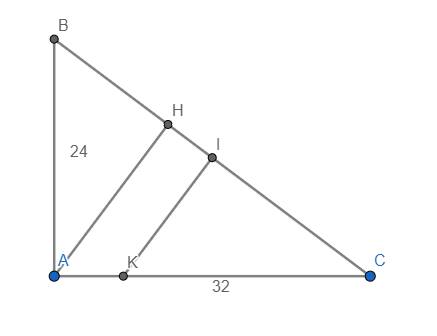
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\)) 

Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)

Nên \(\widehat{HAC}\approx53,13^o\)

Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm

\(\Rightarrow IB=IC=20cm\)

Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\) 

\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)

Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)

Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)

\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)

Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)

Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)

\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)

Biểu thức đã cho lớn nhất khi x + √x + 1 nhỏ nhất

ĐKXĐ: x ≥ 0

⇒ x + √x + 1 ≥ 1

⇒ x + √x + 1 nhỏ nhất là 1 khi x = 0

Vậy giá trị lớn nhất của biểu thức đã cho là 5/1 = 5 khi x = 0

Biểu thức đã cho lớn nhất khi x + √x + 1 nhỏ nhất

ĐKXĐ: x ≥ 0

⇒ x + √x + 1 ≥ 1

⇒ x + √x + 1 nhỏ nhất là 1 khi x = 0

Vậy giá trị lớn nhất của biểu thức đã cho là 5/1 = 5 khi x = 0

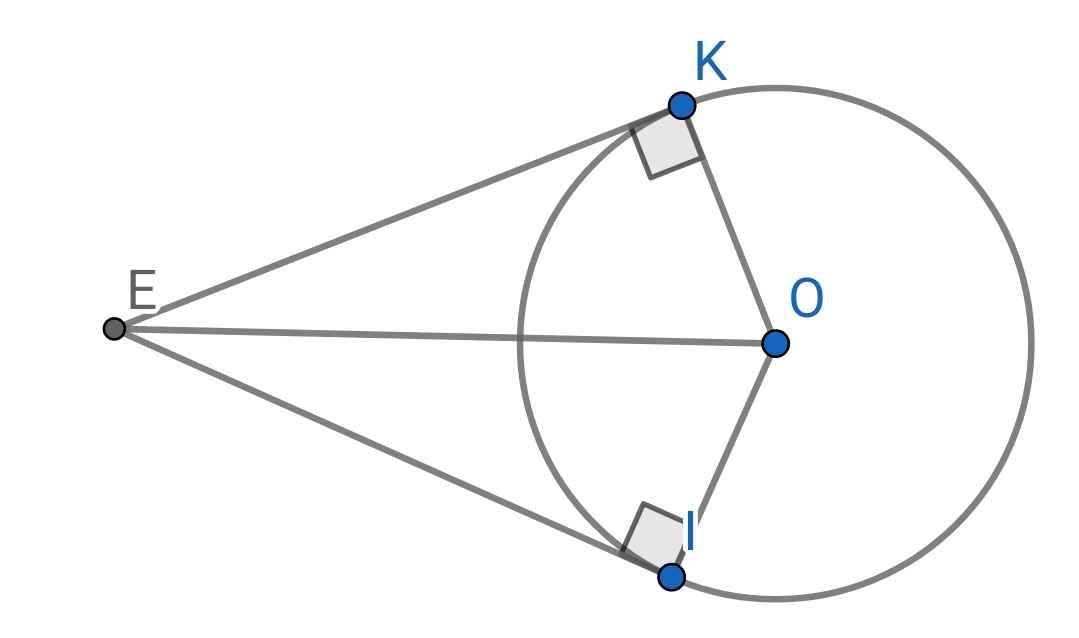  Do EI là tiếp tuyến của (O) tại I

⇒ EI OI

⇒ ∆OEI vuông tại I

⇒ O, E, I cùng thuộc đường tròn đường kính OE  (1)

Do EK là tiếp tuyến của (O) tại K

⇒ EK OK

⇒ ∆OEK vuông tại K

⇒ O, E, K cùng thuộc đường tròn đường kính OE  (2)

Từ (1) và (2) suy ra E, I, O, K cùng thuộc đường tròn đường kính OE