13x 9- 26x 12+ 13x 18+ 39x 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải
Nếu kéo đáy thêm thì diện tích tăng :
\(\dfrac{4x10}{2}\)= 20 ( m2 )
Đ/s : 20 m2


| HGFEW23RTHJHGTREERTHT | E4567UIKJHGTFREWQWERTYU |
| asdcbnjkl;';loiuytrewq | ERTYUIOP;POIU7Y6T5REWQqưer5t6y7u8i9oiuytrewqQ |
| RT6Y7UIUYTREWQWERTYUIUYTR | ƯUYTREERTYUIUYTREWQWERTYUI |

Đây là toán nâng cao chuyên đề trung bình cộng, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng toán tổng hiệu như sau:
Giải:
Tổng số xăng của hàng bán được trong hai tuần là:
11500 x 2 = 23000 (l)
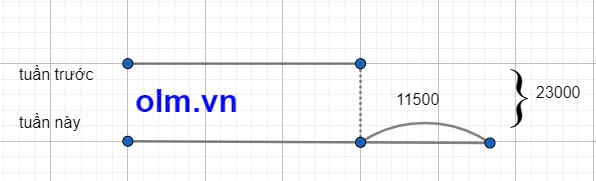
Ta có sơ đồ:
Theo sơ đồ ta có:
Số xăng tuần này bán được là: (23000 + 11500) : 2 = 17250 (l)
Số xăng tuần trước bán được là: 23000 - 17250 = 5750 (l)
Đáp số: Tuần trước bán 5750 l xăng
Tuần này bán 17250 l xăng


Giải:
Bên đĩa cân đặt các quả cân có số cân nặng là:
500 + 200 + 100 = 800 (gam)
Vì cân thăng bằng nên 4 quả táo nặng là 800 gam
Chọn B.800 gam

Giải:
Vì 34 : 6 = 5 dư 4
Vậy lớp 3 có ít nhất số nhóm là:
5 + 1 = 6 (nhóm)
Trong đó có 1 nhóm có 4 học sinh, số nhóm còn lại mỗi nhóm có 5 học sinh
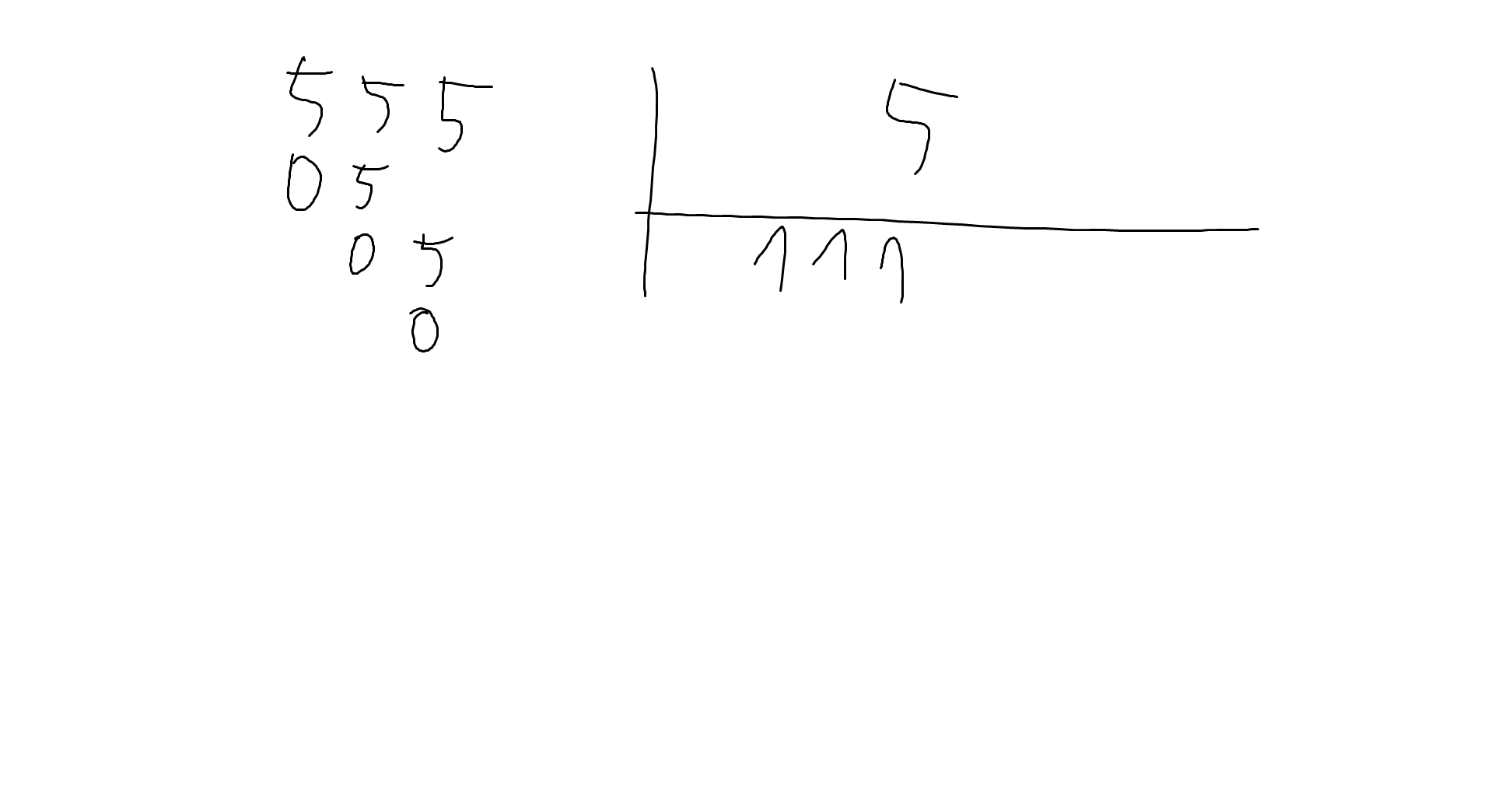
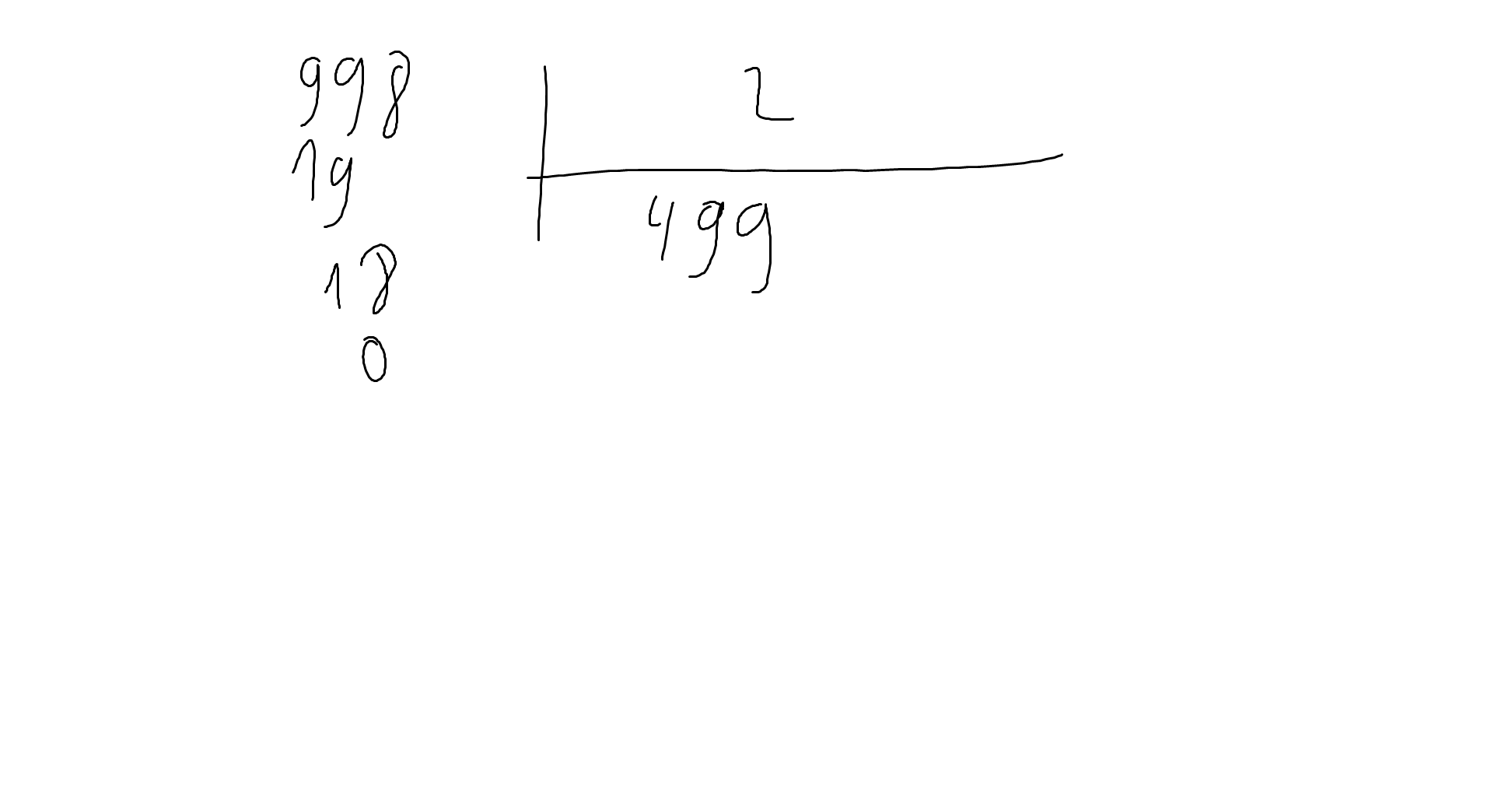
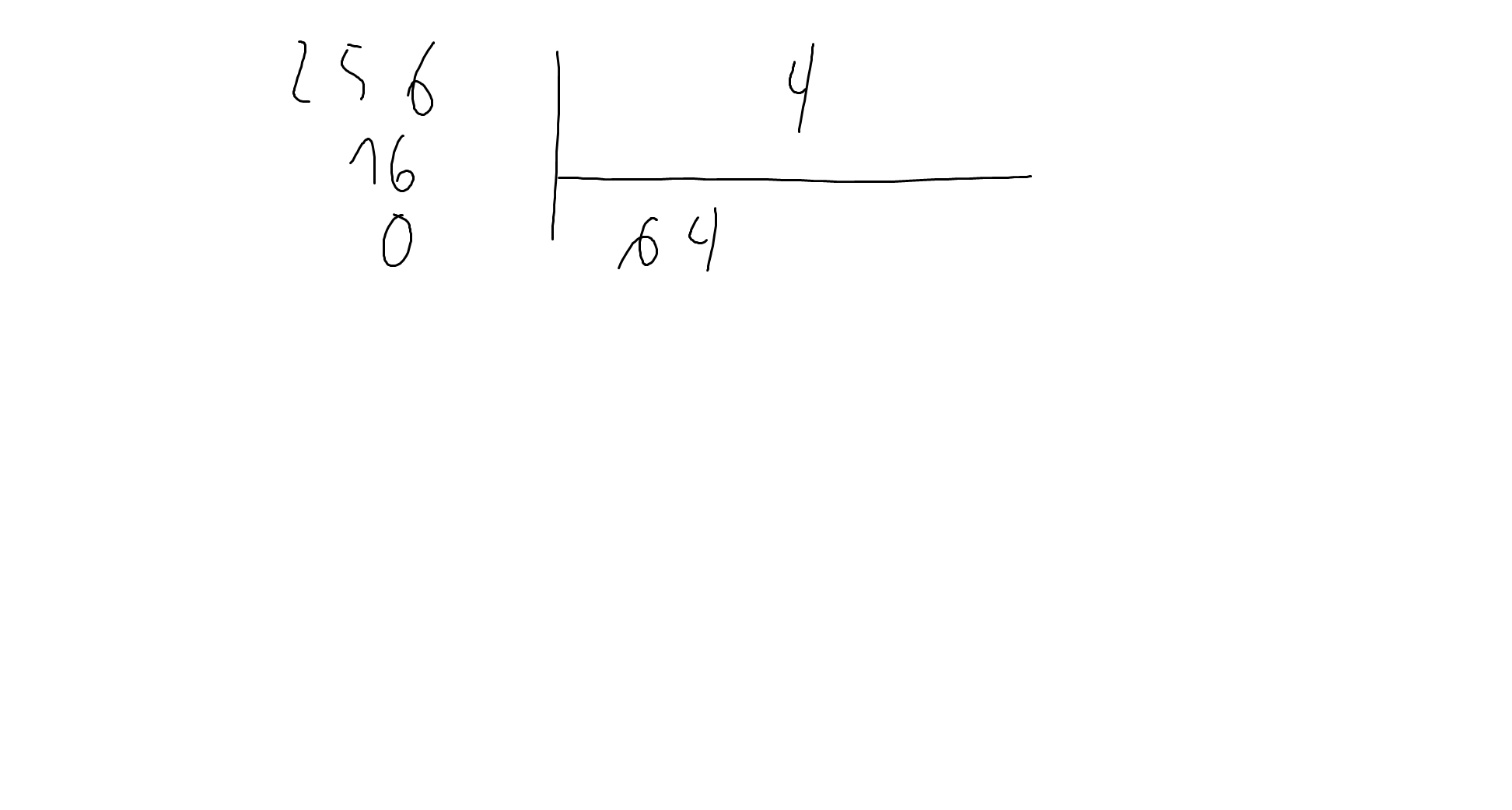
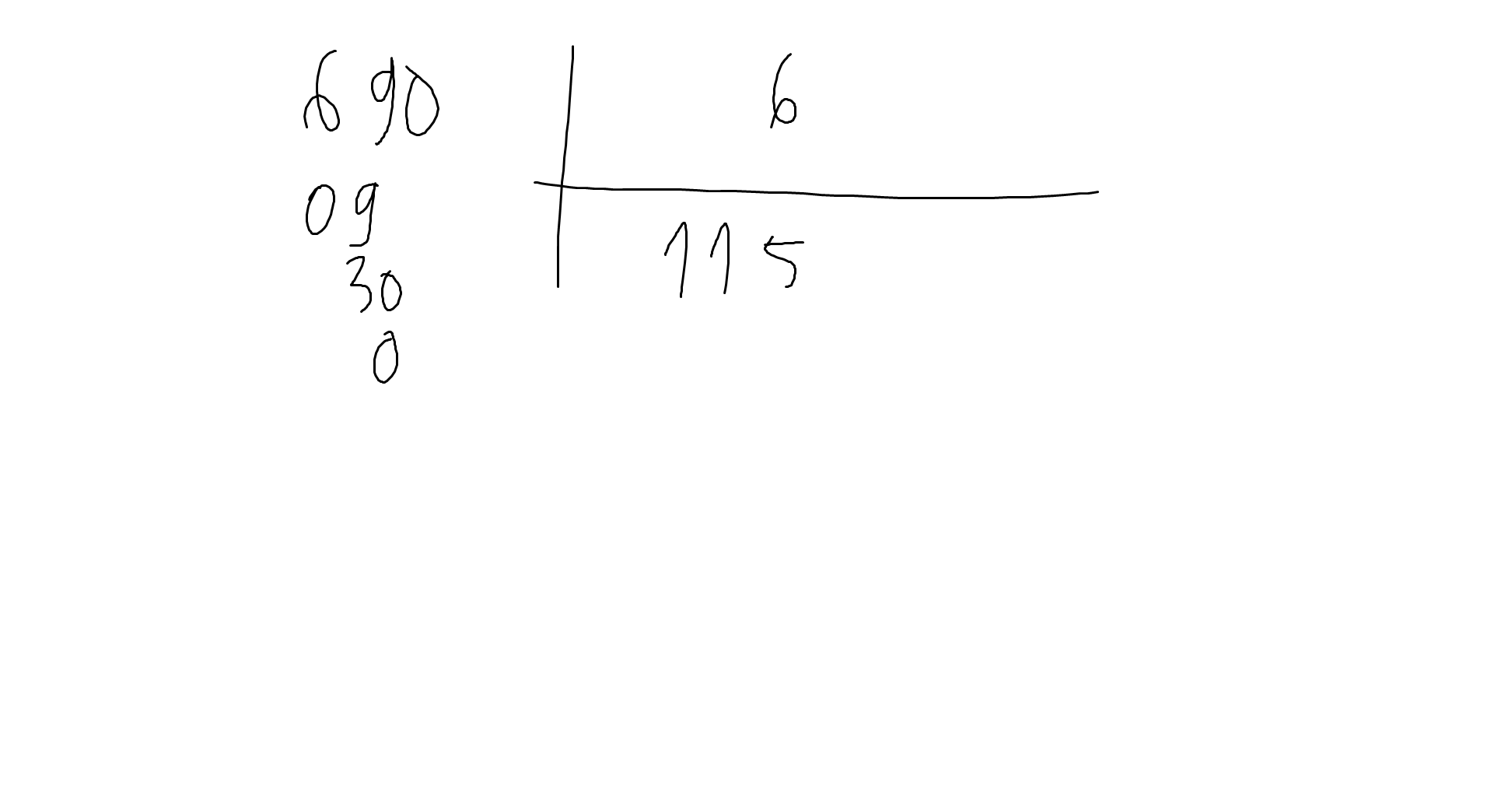
13x9-26x12+13x18+39x9
=13x9-13x24+13x18+13x27
=13x(9-24+18+27)
=13x(-15+45)
=13x30
=390
13 x 9 - 26 x 12 + 13 x 18 + 39 x 9
= 13 x 9 - 13 x 2 x 12 + 13 x 18 + 13 x 3 x 9
= 13 x (9 - 2 x 12 + 18 + 3 x 9)
= 13 x (9 - 24 + 18 + 27)
= 13 x [(27 - 24)+ (9 + 18)]
= 13 x [3 + 27]
= 13 x 30
= 390