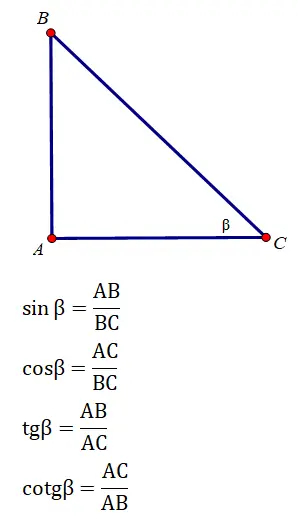
Cho tam giác ABC vuông tại A có 2 cạnh góc vuông có tỉ lệ là 5:6.Tính tỉ số lượng giác của góc B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LT
3
CV
1
PN
7 tháng 8 2020
bạn có thể dùng bđt phụ này :
\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
và đây là cách chứng minh
Bất đẳng thức tương đương :
\(a^2+b^2+a^2+b^2\ge a^2+b^2+2ab\)
\(< =>a^2+b^2\ge2ab\)
\(< =>\left(a-b\right)^2\ge0\)*đúng*
M
0
LT
2
TT
6 tháng 8 2020
Sửa đề :
\(P=\sqrt{x+5+2\sqrt{x+4}}-\sqrt{x+5-2\sqrt{x+4}}\)\(\left(x\ge-4\right)\)
\(=\sqrt{\left(x+4\right)+2\sqrt{x+4}+1}-\sqrt{\left(x+4\right)-2\sqrt{x+4}+1}\)
\(=\sqrt{\left(\sqrt{x+4}+1\right)^2}-\sqrt{\left(\sqrt{x+4}-1\right)^2}\)
\(=\left|\sqrt{x+4}+1\right|-\left|\sqrt{x+4}-1\right|\)
\(=\sqrt{x+4}+1-\sqrt{x+4}+1=2\)
Vậy \(P=2\)
6 tháng 8 2020
\(A=\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}\)
\(A=\sqrt{5-2\sqrt{5}+1}-\sqrt{5+2\sqrt{5}+1}\)
\(A=\sqrt{\left(\sqrt{5}-1\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(A=\sqrt{5}-1-\sqrt{5}-1\)
\(A=-2\)
\(B=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(B=\sqrt{5+4\sqrt{5}+4}-\sqrt{5-4\sqrt{5}+4}\)
\(B=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(B=\sqrt{5}+2-\sqrt{5}+2\)
\(B=4\)
Học tốt
6 tháng 8 2020
Bài làm:
a) \(A=\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}\)
\(A=\sqrt{5-2\sqrt{5}+1}-\sqrt{5+2\sqrt{5}+1}\)
\(A=\sqrt{\left(\sqrt{5}-1\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(A=\sqrt{5}-1-\sqrt{5}-1=-2\)
b) \(B=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(B=\sqrt{4+4\sqrt{5}+5}-\sqrt{4-4\sqrt{5}+5}\)
\(B=\sqrt{\left(2+\sqrt{5}\right)^2}-\sqrt{\left(2-\sqrt{5}\right)^2}\)
\(B=2+\sqrt{5}-\sqrt{5}+2\)
\(B=4\)
LT
2
6 tháng 8 2020
Bài làm:
a) \(\sqrt{x^2+6x+9}=4\)
\(\Leftrightarrow\sqrt{\left(x+3\right)^2}=4\)
\(\Leftrightarrow\left|x+3\right|=4\)
\(\Leftrightarrow\orbr{\begin{cases}x+3=4\\x+3=-4\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-7\end{cases}}\)
b) \(\sqrt{x^2+4x+4}=x-3\)
\(\Leftrightarrow\sqrt{\left(x+2\right)^2}=x-3\)
\(\Leftrightarrow\left|x+2\right|=x-3\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=x-3\\x+2=3-x\end{cases}}\Leftrightarrow\orbr{\begin{cases}0x=-5\left(vl\right)\\2x=1\end{cases}}\Rightarrow x=\frac{1}{2}\)
PN
6 tháng 8 2020
cách khác
a,\(\sqrt{x^2+6x+9}=4\)
\(< =>x^2+6x+9=16\)
\(< =>x^2-x+7x-7=0\)
\(< =>x\left(x-1\right)+7\left(x-1\right)=0\)
\(< =>\left(x+7\right)\left(x-1\right)=0\)
\(< =>\orbr{\begin{cases}x=-7\\x=1\end{cases}}\)
b,\(\sqrt{x^2+4x+4}=x-3\)
\(< =>x^2+4x+4=x^2-6x+9\)
\(< =>x^2+4x+4-x^2+6x-9=0\)
\(< =>10x-5=0< =>x=\frac{1}{2}\)