2 người cùng làm chung 1 công việc thì 4 ngày xong nhưng làm được 2 ngày đầu thì người thứ nhất chuyển đi, người 2 tiếp tục nhưng 6 ngày nữa mới xong. Hỏi làm 1 mình thì bao lâu nữa mới xong?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1:
a: ĐKXĐ: \(x\notin\left\{-2;2;0\right\}\)
\(\dfrac{0,5x^2+x+2}{1+0,5x}:\dfrac{x^3-8}{x+2}+\dfrac{2}{x\left(2-x\right)}\)
\(=\dfrac{0,5\left(x^2+2x+4\right)}{0,5\left(x+2\right)}\cdot\dfrac{x+2}{\left(x-2\right)\left(x^2+2x+4\right)}-\dfrac{2}{x\left(x-2\right)}\)
\(=\dfrac{1}{x-2}-\dfrac{2}{x\left(x-2\right)}=\dfrac{x-2}{x\left(x-2\right)}=\dfrac{1}{x}\)
b: \(P< =\dfrac{1}{1-x}\)
=>\(\dfrac{1}{x}< =\dfrac{1}{1-x}\)
=>\(\dfrac{1}{x}-\dfrac{1}{1-x}< =0\)
=>\(\dfrac{1-x-x}{x\left(1-x\right)}< =0\)
=>\(\dfrac{2x-1}{x\left(x-1\right)}< =0\)
TH1: \(\left\{{}\begin{matrix}2x-1< =0\\x\left(x-1\right)>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{1}{2}\\\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow x< 0\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< 0\\x\ne-2\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}2x-1>=0\\x\left(x-1\right)< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{2}\\0< x< 1\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}< =x< 1\)

a: Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 4 chấm" là: \(\dfrac{22}{40}=\dfrac{11}{20}\)
b: Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc sắc là mặt 6 chấm" là \(\dfrac{10}{18}=\dfrac{5}{9}\)
c: Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc sắc là mặt 1 chấm" là \(\dfrac{18}{40}=\dfrac{9}{20}\)
d: Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc sắc là mặt 3 chấm" là \(\dfrac{14}{20}=\dfrac{7}{10}\)
e: Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc sắc là mặt 5 chấm" là \(\dfrac{15}{45}=\dfrac{1}{3}\)
f: Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc sắc là mặt 2 chấm" là \(\dfrac{6}{24}=\dfrac{1}{4}\)

a.
Xét hai tam giác AHB và CAB có:
\(\left\{{}\begin{matrix}\widehat{B}-chung\\\widehat{AHB}=\widehat{CAB}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta AHB\sim\Delta CAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BH}{AB}\Rightarrow AB^2=BH.BC\)
b.
Do H là trung điểm BM, trong tam giác ABM có AH vừa là đường cao đồng thời là trung tuyến
\(\Rightarrow\Delta ABM\) cân tại A \(\Rightarrow\widehat{ABH}=\widehat{AMH}\)
Mà \(\widehat{AMH}=\widehat{CMK}\) (đối đỉnh)
\(\Rightarrow\widehat{ABH}=\widehat{CMK}\)
Xét hai tam giác ABH và CMK có:
\(\left\{{}\begin{matrix}\widehat{ABH}=\widehat{CMK}\left(cmt\right)\\\widehat{AHB}=\widehat{CKM}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABH\sim\Delta CMK\left(g.g\right)\)
c.
Xét hai tam giác AMH và CMK có:
\(\left\{{}\begin{matrix}\widehat{AHM}=\widehat{CKM}=90^0\\\widehat{AMH}=\widehat{CMK}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMH\sim\Delta CMK\left(g.g\right)\Rightarrow\dfrac{AM}{CM}=\dfrac{MH}{MK}\)
\(\Rightarrow\dfrac{AM}{MH}=\dfrac{CM}{MK}\)
Xét hai tam giác AMC và HMK có:
\(\left\{{}\begin{matrix}\dfrac{AM}{MH}=\dfrac{CM}{MK}\left(cmt\right)\\\widehat{AMC}=\widehat{HMK}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMC\sim\Delta HMK\left(c.g.c\right)\)
\(\Rightarrow\dfrac{AM}{MH}=\dfrac{AC}{HK}\Rightarrow MH.AC=AM.HK\)
Mà H là trung điểm BM \(\Rightarrow MH=\dfrac{1}{2}BM\)
\(\Rightarrow\dfrac{1}{2}BM.AC=AM.HK\Rightarrow BM.AC=2AM.HK\)
d.
Từ câu c, do \(\Delta AMC\sim \Delta HMK\Rightarrow \widehat{ACM}=\widehat{HKM}\)
Mà \(\left\{{}\begin{matrix}\widehat{ACM}+\widehat{CAI}=90^0\\\widehat{HKM}+\widehat{HKI}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{CAI}=\widehat{HKI}\)
Xét hai tam giác CAI và HKI có:
\(\left\{{}\begin{matrix}\widehat{I}-chung\\\widehat{CAI}=\widehat{HKI}\end{matrix}\right.\) \(\Rightarrow\Delta CAI\sim\Delta HKI\left(g.g\right)\)
\(\Rightarrow\dfrac{CI}{HI}=\dfrac{AI}{KI}\Rightarrow KI.CI=HI.AI\)
Ta có:
\(AC^2=AK^2+KC^2=AI^2-IK^2+KC^2\)
\(=AI\left(AH+HI\right)-IK^2+KC^2\)\(=AH.AI+AI.HI-IK^2+KC^2\)
\(=AH.AI+KI.CI-IK^2+KC^2=AH.AI+KI\left(CI-IK\right)+KC^2\)
\(=AH.AI+KI.CK+KC^2=AH.AI+CK.\left(KI+CK\right)\)
\(=AH.AI+CK.CI\) (đpcm)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
b: Xét ΔABM có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABM cân tại A
=>\(\widehat{AMB}=\widehat{ABM}\)
mà \(\widehat{AMB}=\widehat{CMK}\)(hai góc đối đỉnh)
nên \(\widehat{ABM}=\widehat{CMK}\)
Xét ΔHBA vuông tại H và ΔKMC vuông tại K có
\(\widehat{HBA}=\widehat{KMC}\)
Do đó: ΔHBA~ΔKMC
d: Gọi N là giao điểm của IM với CA
Xét ΔCAI có
AK,CH là các đường cao
AK cắt CH tại M
Do đó: M là trực tâm của ΔCAI
=>IM\(\perp\)CA tại N
Xét ΔCKA vuông tại K và ΔCNI vuông tại N có
\(\widehat{KCA}\) chung
Do đó: ΔCKA~ΔCNI
=>\(\dfrac{CK}{CN}=\dfrac{CA}{CI}\)
=>\(CK\cdot CI=CA\cdot CN\)
Xét ΔAHC vuông tại H và ΔANI vuông tại N có
\(\widehat{HAC}\) chung
Do đó: ΔAHC~ΔANI
=>\(\dfrac{AH}{AN}=\dfrac{AC}{AI}\)
=>\(AH\cdot AI=AN\cdot AC\)
\(CK\cdot CI+AH\cdot AI\)
\(=AN\cdot AC+CN\cdot AC\)
\(=AC\left(AN+CN\right)=AC^2\)

Gọi độ dài quãng đường AB là x (km) với x>0
Thời gian người đó đi từ A đến B là: \(\dfrac{x}{35}\) giờ
Do lúc về đi con đường khác dài hơn đường cũ 8km nên độ dài quãng đường về là: \(x+8\) (km)
Vận tốc lúc về lớn hơn lúc đi là 5km/h nên vận tốc lúc về là: \(35+5=40\) (km/h)
Thời gian về là: \(\dfrac{x+8}{40}\) gờ
Do thời gian về ít hơn thời gian đi là 3 phút =1/20 giờ nên ta có pt:
\(\dfrac{x}{35}-\dfrac{x+8}{40}=\dfrac{1}{20}\)
\(\Leftrightarrow x\left(\dfrac{1}{35}-\dfrac{1}{40}\right)=\dfrac{8}{40}+\dfrac{1}{20}\)
\(\Leftrightarrow\dfrac{x}{280}=\dfrac{1}{4}\)
\(\Leftrightarrow x=\dfrac{280}{4}=70\left(km\right)\)

\(A=2010\left(\dfrac{4x-3}{x^2+1}\right)=2010\left(\dfrac{-4\left(x^2+1\right)+4x^2+4x+1}{x^2+1}\right)\)
\(=2010\left(-4+\dfrac{\left(2x+1\right)^2}{x^2+1}\right)\ge-4.2010=-8040\)
\(A_{min}=-8040\) khi \(2x+1=0\Rightarrow x=-\dfrac{1}{2}\)

Giải phương trình bậc nhất một ẩn có dạng ax + b = 0 có thể gặp một số khó khăn tùy thuộc vào giá trị của các hệ số a và b. Dưới đây là một số khó khăn phổ biến:
1.Phương trình vô nghiệm: Nếu hệ số a = 0 và b ≠ 0, phương trình sẽ không có nghiệm vì không thể chia một số khác không. Trong trường hợp này, phương trình biểu diễn một mệnh đề vô lí.
2.Vô số nghiệm: Nếu cả a và b đều bằng 0, phương trình có vô số nghiệm vì mọi giá trị của x đều là nghiệm.
3.Chia cho 0: Khi a = 0 và b = 0, bạn sẽ phải chia cho 0 khi cố gắng giải phương trình. Điều này không xác định và không có nghiệm.
4.Dạng phức của nghiệm: Nếu các hệ số a và b là số phức, phương trình có thể có nghiệm ở dạng số phức, điều này có thể tạo thêm khó khăn cho việc giải bằng phương pháp truyền thống.
5.Tính biến đổi: Trong một số trường hợp, phương trình có thể được biến đổi thành dạng khác, khiến cho quá trình giải trở nên phức tạp hơn.
Mặc dù giải phương trình bậc nhất là một công việc đơn giản, nhưng cần lưu ý đến những trường hợp đặc biệt và cẩn thận khi xử lý để tránh sai sót và hiểu rõ về tự nhiên của các nghiệm có thể xuất hiện.
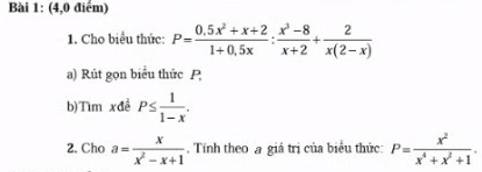








Gọi thời gian người 1 và người 2 hoàn thành công việc khi làm một mình lần lượt là x(ngày) và y(ngày)
(ĐK: x>0; y>0)
Trong 1 ngày, người 1 làm được \(\dfrac{1}{x}\left(côngviệc\right)\)
Trong 1 ngày, người 2 làm được \(\dfrac{1}{y}\left(côngviệc\right)\)
Trong 1 ngày, hai người làm được \(\dfrac{1}{4}\left(côngviệc\right)\)
Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Trong 2 ngày, người 1 làm được \(\dfrac{2}{x}\)(công việc)
Trong 2+6=8 ngày, người 2 làm được \(\dfrac{8}{y}\)(công việc)
Vì làm được 2 ngày thì người 1 chuyển đi, người 2 làm tiếp trong 6 ngày thì xong công việc nên ta có: \(\dfrac{2}{x}+\dfrac{8}{y}=1\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{2}{x}+\dfrac{8}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{2}\\\dfrac{2}{x}+\dfrac{8}{y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{6}{y}=-\dfrac{1}{2}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\\dfrac{1}{x}=\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{1}{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=6\\y=12\end{matrix}\right.\)(nhận)
Vậy: thời gian người 1 và người 2 hoàn thành công việc khi làm một mình lần lượt là 6 ngày và 12 ngày
Giải:
Trong một ngày hai người cùng làm được:
1 : 4 = \(\dfrac{1}{4}\) (công việc)
Hai ngày hai người cùng làm được:
\(\dfrac{1}{4}\) x 2 = \(\dfrac{1}{2}\) (công việc)
Trong 6 ngày người thứ hai làm một mình được:
1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\) (công việc)
Trong một ngày người thứ hai làm một mình được:
\(\dfrac{1}{2}\) : 6 = \(\dfrac{1}{12}\) (công việc)
Trong một ngày người thứ nhất làm một mình được:
\(\dfrac{1}{4}\) - \(\dfrac{1}{12}\) = \(\dfrac{1}{6}\) (công việc)
Người thứ nhất làm một mình sẽ hoàn thành công việc sau:
1 : \(\dfrac{1}{6}\) = 6 (ngày)
Kết luận: người thứ nhất làm một mình sẽ xong công việc sau 6 ngày