Cho tứ giác ABCD có AC và BD cắt nhau tại I. Qua I, kẻ đường thẳng song song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F. a) Chứng minh FE // BD. b) Từ 1 kẻ đường thẳng song song với AB cắt BC tại G và đường thẳng song song với AD cắt CE tại H. Chứng minh rằng CG.DH = BG.CH.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Ta có: AK=KO=OH
=>\(AK=KO=OH=\dfrac{1}{3}AH\)
=>\(AO=\dfrac{2}{3}AH;AK=\dfrac{1}{3}AH\)
Xét ΔAHB có EK//BH
nên \(\dfrac{AE}{AB}=\dfrac{AK}{AH}\)
=>\(\dfrac{AE}{AB}=\dfrac{1}{3}\)
Xét ΔABH có MO//BH
nên \(\dfrac{AM}{AB}=\dfrac{AO}{AH}\)
=>\(\dfrac{AM}{AB}=\dfrac{2}{3}\)
Xét ΔABC có EF//BC
nên \(\dfrac{EF}{BC}=\dfrac{AE}{AB}\)
=>\(\dfrac{EF}{BC}=\dfrac{1}{3}\)
=>\(EF=\dfrac{BC}{3}=\dfrac{30}{3}=10\left(cm\right)\)
Xét ΔABC có MP//BC
nên \(\dfrac{MP}{BC}=\dfrac{AM}{AB}\)
=>\(\dfrac{MP}{30}=\dfrac{2}{3}\)
=>\(MP=20\left(cm\right)\)
b: Xét ΔAMP và ΔABC có
\(\widehat{AMP}=\widehat{ABC}\)(hai góc đồng vị, MP//BC)
\(\widehat{MAP}\) chung
Do đó: ΔAMP~ΔABC
=>\(\dfrac{S_{AMP}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2\)
=>\(\dfrac{S_{AMP}}{10.8}=\dfrac{4}{9}\)
=>\(S_{AMP}=4,8\left(dm^2\right)\)
Xét ΔAEF và ΔABC có
\(\widehat{AEF}=\widehat{ABC}\)(hai góc đồng vị, EF//BC)
\(\widehat{FAE}\) chung
Do đó: ΔAEF~ΔABC
=>\(\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=\dfrac{1}{9}\)
=>\(S_{AEF}=\dfrac{10.8}{9}=1,2\left(dm^2\right)\)
Ta có: \(S_{AEF}+S_{MEFP}=S_{AMP}\)
=>\(S_{MEFP}+1,2=4,8\)
=>\(S_{MEFP}=3,6\left(dm^2\right)\)

\(A=\dfrac{2}{6x-5-9x^2}\)
\(=\dfrac{2}{-9x^2+6x-5}\)
\(=\dfrac{2}{-\left(9x^2-6x+5\right)}\)
\(=\dfrac{2}{-\left(9x^2-6x+1+4\right)}\)
\(=\dfrac{2}{-\left(3x-1\right)^2-4}\)
\(\left(3x-1\right)^2>=0\forall x\)
=>\(-\left(3x-1\right)^2< =0\forall x\)
=>\(-\left(3x-1\right)^2-4< =-4\forall x\)
=>\(A=\dfrac{2}{-\left(3x-1\right)^2-4}>=\dfrac{2}{-4}=-\dfrac{1}{2}\forall x\)
Dấu '=' xảy ra khi 3x-1=0
=>3x=1
=>\(x=\dfrac{1}{3}\)

a: Xét ΔAEH vuông tại E và ΔAHC vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHC
b: Ta có: ΔAEH vuông tại E
=>\(EH^2+EA^2=AH^2\)
=>\(EH^2=10^2-6^2=64=8^2\)
=>EH=8(cm)
Xét ΔAHE có AM là phân giác
nên \(\dfrac{MH}{AH}=\dfrac{ME}{AE}\)
=>\(\dfrac{MH}{10}=\dfrac{ME}{6}\)
=>\(\dfrac{MH}{5}=\dfrac{ME}{3}\)
mà MH+ME=EH=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MH}{5}=\dfrac{ME}{3}=\dfrac{MH+ME}{5+3}=\dfrac{8}{8}=1\)
=>MH=5(cm); ME=3(cm)
c: Xét ΔHEC có HN là phân giác
nên \(\dfrac{EN}{NC}=\dfrac{EH}{HC}\left(1\right)\)
Xét ΔAHE có AM là phân giác
nên \(\dfrac{EM}{MH}=\dfrac{EA}{AH}\left(2\right)\)
Xét ΔEHA vuông tại E và ΔHCA vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔEHA~ΔHCA
=>\(\dfrac{EA}{HA}=\dfrac{EH}{HC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{EM}{MH}=\dfrac{EN}{NC}\)
Xét ΔEHC có \(\dfrac{EM}{MH}=\dfrac{EN}{NC}\)
nên MN//HC
=>MN//BC
mà AH\(\perp\)BC
nên HA\(\perp\)MN
Xét ΔAHN có
NM,HE là các đường cao
NM cắt HE tại M
Do đó: M là trực tâm của ΔAHN
=>AM\(\perp\)HN

Gọi số tự nhiên ban đầu là X
Viết thêm chữ số 2 vào bên trái và một chữ số 2 vào bên phải thì số mới sẽ là 10X+2000+2=10X+2002
Số mới gấp 153 lần số ban đầu nên ta có:
10X+2002=153X
=>143X=2002
=>\(X=\dfrac{2002}{143}=14\left(nhận\right)\)
Vậy: Số cần tìm là 14

Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian dự kiến ban đầu là \(\dfrac{x}{40}\left(giờ\right)\)
Thời gian đi nửa quãng đường ban đầu là \(\dfrac{x}{2}:40=\dfrac{x}{80}\left(giờ\right)\)
vận tốc trên nửa quãng đường còn lại là 40+10=50(km/h)
Thời gian đi nửa quãng đường còn lại là \(\dfrac{x}{2}:50=\dfrac{x}{100}\left(giờ\right)\)
Tổng thời gian là 11h30p-6h30p-30p=4h30p=4,5(giờ)
Theo đề, ta có phương trình:
\(\dfrac{x}{80}+\dfrac{x}{100}=4,5\)
=>\(\dfrac{9x}{400}=4,5\)
=>\(9x=400\cdot4,5=1800\)
=>\(x=\dfrac{1800}{9}=200\left(nhận\right)\)
vậy: Quãng đường AB là 200km

a: \(P=\dfrac{x}{x-2}+\dfrac{2-x}{x+2}+\dfrac{8-6x}{x^2-4}\)
\(=\dfrac{x}{x-2}-\dfrac{x-2}{x+2}+\dfrac{8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x+2\right)-\left(x-2\right)^2+8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x-x^2+4x-4+8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{x^2-4}\)
b: Thay x=3 vào P, ta được:
\(P=\dfrac{4}{3^2-4}=\dfrac{4}{5}\)
Thay x=-1/2 vào P, ta được:
\(P=\dfrac{4}{\left(-\dfrac{1}{2}\right)^2-4}=\dfrac{4}{\dfrac{1}{4}-4}=4:\dfrac{-15}{4}=\dfrac{-16}{15}\)
c: Để P là số nguyên thì \(4⋮x^2-4\)
=>\(x^2-4\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x^2\in\left\{5;3;6;2;8;0\right\}\)
mà x nguyên
nên x^2=0
=>x=0(nhận)

Gọi thời gian người 1 và người 2 hoàn thành công việc khi làm một mình lần lượt là x(ngày) và y(ngày)
(ĐK: x>0; y>0)
Trong 1 ngày, người 1 làm được \(\dfrac{1}{x}\left(côngviệc\right)\)
Trong 1 ngày, người 2 làm được \(\dfrac{1}{y}\left(côngviệc\right)\)
Trong 1 ngày, hai người làm được \(\dfrac{1}{4}\left(côngviệc\right)\)
Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Trong 2 ngày, người 1 làm được \(\dfrac{2}{x}\)(công việc)
Trong 2+6=8 ngày, người 2 làm được \(\dfrac{8}{y}\)(công việc)
Vì làm được 2 ngày thì người 1 chuyển đi, người 2 làm tiếp trong 6 ngày thì xong công việc nên ta có: \(\dfrac{2}{x}+\dfrac{8}{y}=1\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{2}{x}+\dfrac{8}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{2}\\\dfrac{2}{x}+\dfrac{8}{y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{6}{y}=-\dfrac{1}{2}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\\dfrac{1}{x}=\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{1}{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=6\\y=12\end{matrix}\right.\)(nhận)
Vậy: thời gian người 1 và người 2 hoàn thành công việc khi làm một mình lần lượt là 6 ngày và 12 ngày
Giải:
Trong một ngày hai người cùng làm được:
1 : 4 = \(\dfrac{1}{4}\) (công việc)
Hai ngày hai người cùng làm được:
\(\dfrac{1}{4}\) x 2 = \(\dfrac{1}{2}\) (công việc)
Trong 6 ngày người thứ hai làm một mình được:
1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\) (công việc)
Trong một ngày người thứ hai làm một mình được:
\(\dfrac{1}{2}\) : 6 = \(\dfrac{1}{12}\) (công việc)
Trong một ngày người thứ nhất làm một mình được:
\(\dfrac{1}{4}\) - \(\dfrac{1}{12}\) = \(\dfrac{1}{6}\) (công việc)
Người thứ nhất làm một mình sẽ hoàn thành công việc sau:
1 : \(\dfrac{1}{6}\) = 6 (ngày)
Kết luận: người thứ nhất làm một mình sẽ xong công việc sau 6 ngày

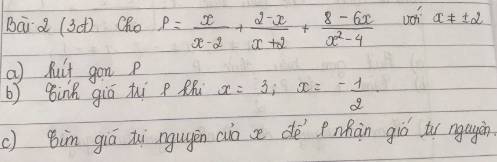
a: Xét ΔABC có EI//BC
nên \(\dfrac{AE}{AB}=\dfrac{AI}{AC}\left(1\right)\)
Xét ΔADC có FI//DC
nên \(\dfrac{AI}{AC}=\dfrac{AF}{AD}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AE}{AB}=\dfrac{AF}{AD}\)
Xét ΔABD có \(\dfrac{AE}{AB}=\dfrac{AF}{AD}\)
nên EF//BD
b: Xét ΔCBA có GI//AB
nên \(\dfrac{CG}{BG}=\dfrac{CI}{IA}\left(3\right)\)
Xét ΔCAD có IH//AD
nên \(\dfrac{CI}{IA}=\dfrac{CH}{HD}\left(4\right)\)
Từ (3),(4) suy ra \(\dfrac{CG}{BG}=\dfrac{CH}{HD}\)
=>\(CG\cdot HD=BG\cdot CH\)