\(11x+42-2x=100-9x-22\\ 11x-2x+9x=100-22-42\\ 18x=36\\ x=\dfrac{36}{18}=2\)

x=2

1: Xét ΔADH vuông tại D và ΔAHB vuông tại H có

\(\widehat{DAH}\) chung

Do đó: ΔADH~ΔAHB

2: Xét ΔEHA vuông tại E và ΔECH vuông tại E có

\(\widehat{EHA}=\widehat{ECH}\left(=90^0-\widehat{EHC}\right)\)

Do đó: ΔEHA~ΔECH

=>\(\dfrac{EH}{EC}=\dfrac{EA}{EH}\)

=>\(EH^2=EA\cdot EC\)

3: Xét ΔAEH vuông tại E và ΔAHC vuông tại H có

\(\widehat{EAH}\) chung

Do đó: ΔAEH~ΔAHC

=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)

=>\(AE\cdot AC=AH^2\left(1\right)\)

Ta có: ΔADH~ΔAHB

=>\(\dfrac{AD}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AD\cdot AB\left(2\right)\)

Từ (1) và (2) suy ra \(AE\cdot AC=AD\cdot AB\)

=>\(\dfrac{AE}{AD}=\dfrac{AB}{AC}\)

Xét ΔAEB và ΔADC có

\(\dfrac{AE}{AD}=\dfrac{AB}{AC}\)

\(\widehat{EAB}\) chung

Do đó: ΔAEB~ΔADC

=>\(\widehat{ABE}=\widehat{ACD}\)

Xét ΔMBD và ΔMCE có

\(\widehat{MBD}=\widehat{MCE}\)

\(\widehat{DMB}=\widehat{EMC}\)(hai góc đối đỉnh)

Do đó: ΔMBD~ΔMCE

 a) Tam giác MNP có các đường cao MK, NI cắt nhau tại H nên H là trực tâm tam giác MNP => PH vuông góc MN hay PA vuông góc MN tại A.

 b) Xét 2 tam giác MIN và MAP, ta có:

 \(\widehat{MIN}=\widehat{MAP}=90^o\); \(\widehat{NMP}\) chung

 \(\Rightarrow\Delta MIN\sim\Delta MAP\left(g.g\right)\)

 c) Tương tự câu b), ta chứng minh được \(\Delta PIN\sim\Delta PKM\)

 \(\Rightarrow\dfrac{PI}{PK}=\dfrac{PN}{PM}\Rightarrow\dfrac{PI}{PN}=\dfrac{PK}{PM}\)

 Xét tam giác PIK và PNM, ta có:

 \(\dfrac{PI}{PN}=\dfrac{PK}{PM};\widehat{MPN}\) chung

 \(\Rightarrow\Delta PIK\sim\Delta PNM\left(c.g.c\right)\)

 \(\Rightarrow\widehat{PKI}=\widehat{PMN}\) 

 d) Xét tam giác MIH và MKP, ta có:

 \(\widehat{MIH}=\widehat{MKP}=90^o\); \(\widehat{KMP}\) chung

 \(\Rightarrow\Delta MIH\sim\Delta MKP\left(g.g\right)\)

 \(\Rightarrow\dfrac{MI}{MK}=\dfrac{MH}{MP}\)

 \(\Rightarrow MK.MH=MI.MP\)

 e) Từ c), suy ra \(PK.PN=PI.PM\)

 Do đó \(MH.MK+PK.PN\)

 \(=MI.MP+PI.PM\)

 \(=MP\left(MI+PI\right)\)

 \(=MP^2\), ta có đpcm.

 f) Từ câu d), ta có \(\widehat{PIK}=\widehat{PNM}\)

 Tương tự câu d), ta cũng chứng minh được \(\Delta MIA\sim\Delta MNP\)

 \(\Rightarrow\widehat{MIA}=\widehat{MNP}\)

 \(\Rightarrow90^o-\widehat{MIA}=90^o-\widehat{MNP}\)

 \(\Rightarrow\widehat{AIN}=\widehat{KIN}\)

 \(\Rightarrow\) IN là tia phân giác \(\widehat{AIK}\)

 g) Xét tam giác MBK và MKN, ta có:

 \(\widehat{MBK}=\widehat{MKN}=90^o\); \(\widehat{NMK}\) chung

 \(\Rightarrow\Delta MBK\sim\Delta MKN\left(g.g\right)\)

 \(\Rightarrow\dfrac{MB}{MK}=\dfrac{MK}{MN}\)

 \(\Rightarrow MK^2=MB.MN\)

 Tương tự, ta cũng có \(MK^2=MC.MP\)

 \(\Rightarrow MB.MN=MC.MP\left(=MK^2\right)\)

 \(\Rightarrow\dfrac{MN}{MC}=\dfrac{MP}{MB}\)

 Xét tam giác MNP và MCB, ta có:

 \(\dfrac{MN}{MC}=\dfrac{MP}{MB};\) \(\widehat{NMP}\) chung

 \(\Rightarrow\Delta MNP\sim\Delta MCB\left(c.g.c\right)\)

 \(\Rightarrow\widehat{MNP}=\widehat{MCB}\)

 Theo cmt, ta có \(\widehat{MIA}=\widehat{MNP}\)

 \(\Rightarrow\widehat{MIA}=\widehat{MCB}\)

 \(\Rightarrow\) IA//BC (2 góc đồng vị bằng nhau)

a: Xét ΔMNP có

NI,MK là các đường cao

NI cắt MK tại H

Do đó: H là trực tâm của ΔMNP

=>PH\(\perp\)MN tại A

b: Xét ΔMIN vuông tại I và ΔMAP vuông tại A có

\(\widehat{IMN}\) chung

Do đó: ΔMIN~ΔMAP

c: Xét ΔPKM vuông tại K và ΔPIN vuông tại I có

\(\widehat{KPM}\) chung

Do đó: ΔPKM~ΔPIN

=>\(\dfrac{PK}{PI}=\dfrac{PM}{PN}\)

=>\(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)

Xét ΔPIK và ΔPNM có 

\(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)

\(\widehat{IPK}\) chung

Do đó: ΔPIK~ΔPNM

=>\(\widehat{PKI}=\widehat{PMN}\)

d: Xét ΔMIH vuông tại H và ΔMKP vuông tại K có

\(\widehat{IMH}\) chung

Do đó: ΔMIH~ΔMKP

=>\(\dfrac{MI}{MK}=\dfrac{MH}{MP}\)

=>\(MI\cdot MP=MK\cdot MH\)

e: \(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)

=>\(PI\cdot PM=PN\cdot PK\)

\(MH\cdot MK+PK\cdot PN\)

\(=MI\cdot MP+IP\cdot MP\)

=MP(MI+IP)

=MP^2

a

ta có: MN\(\perp\)AC

AB\(\perp\)AC

Do đó: MN//AB

ta có: MP\(\perp\)AB

AC\(\perp\)AB

Do đó: MP//AC

Xét ΔBMP vuông tại P và ΔMCN vuông tại N có

\(\widehat{MBP}=\widehat{CMN}\)(hai góc đồng vị, MN//AB)

Do đó: ΔBMP~ΔMCN

b: Xét ΔBAC có MP//AC

nên \(\dfrac{MP}{AC}=\dfrac{BM}{BC}\)

=>\(\dfrac{MP}{12}=\dfrac{6}{15}=\dfrac{2}{5}\)

=>\(MP=12\cdot\dfrac{2}{5}=4,8\left(cm\right)\)

Xét ΔCAB có MN//AB

nên \(\dfrac{MN}{AB}=\dfrac{CM}{CB}\)

=>\(\dfrac{MN}{9}=\dfrac{9}{15}=\dfrac{3}{5}\)

=>MN=9*3/5=5,4(cm)

Xét tứ giác APMN có \(\widehat{APM}=\widehat{ANM}=\widehat{PAN}=90^0\)

nên APMN là hình chữ nhật

=>\(AM^2=MN^2+MP^2=5,4^2+4,8^2=52,2\)

=>\(AM=\sqrt{52,2}\left(cm\right)\)

a) \(4x^2-1=\left(2x+1\right)\left(3x-5\right)\)

\(\Leftrightarrow\left(2x\right)^2-1^2=\left(2x+1\right)\left(3x-5\right)\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1\right)-\left(2x+1\right)\left(3x-5\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1-3x+5\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(4-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\4=x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=4\end{matrix}\right.\)

Vậy: ...

b) \(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}=10\)

\(\Leftrightarrow\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}-10=0\)

\(\Leftrightarrow\left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0\)

\(\Leftrightarrow\dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\)

\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\)

\(\Leftrightarrow x-100=0\)

\(\Leftrightarrow x=100\)

Vậy: ... 

a) Bảng giá trị

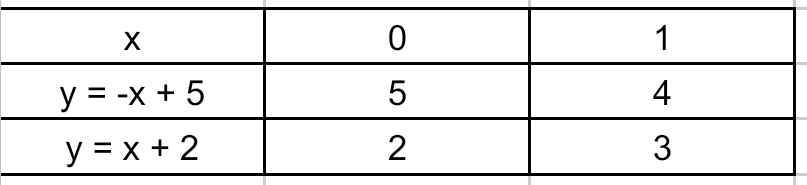  Đồ thị:

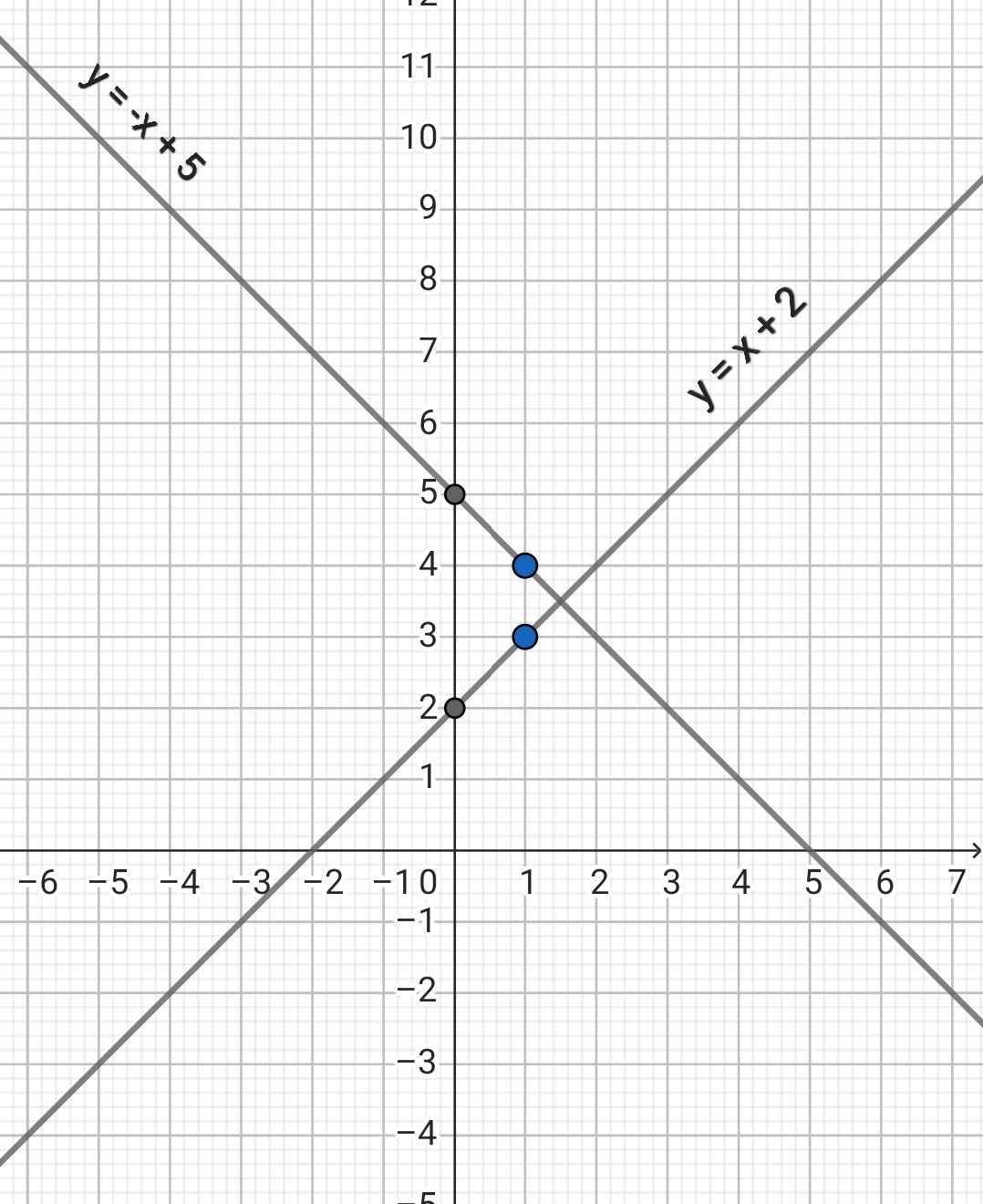
b) Phương trình hoành độ giao điểm của (d₁) và (d₂):

-x + 5 = x + 2

-x - x = 2 - 5

-2x = -3

x = 3/2

Thay x = 3/2 vào (d₂), ta có:

y = 3/2 + 2 = 7/2

Vậy tọa độ giao điểm M(3/2; 7/2)

c) Gọi (d₃): y = ax + b (a ≠ 0) là đồ thị của hàm số cần tìm

Do (d₃) // (d₁) nên a = -1

⇒ (d₃): y = -x + b

Do (d₃) đi qua K(-4; 2) nên thay tọa độ của K(-4; 2) vào (d₃), ta có:

-(-4) + b = 2

b = 2 - 4

b = -2

Vậy hàm số cần tìm là:

y = -x - 2

a) Đồ thị hs:`y=-2x+5` cắt `Ox(5/2;0)` và cắt `Oy(0;5)` 

Đồ thị hs: `y=x+2` cắt `Ox(-2;0)` và cắt `Oy(0;2)` 

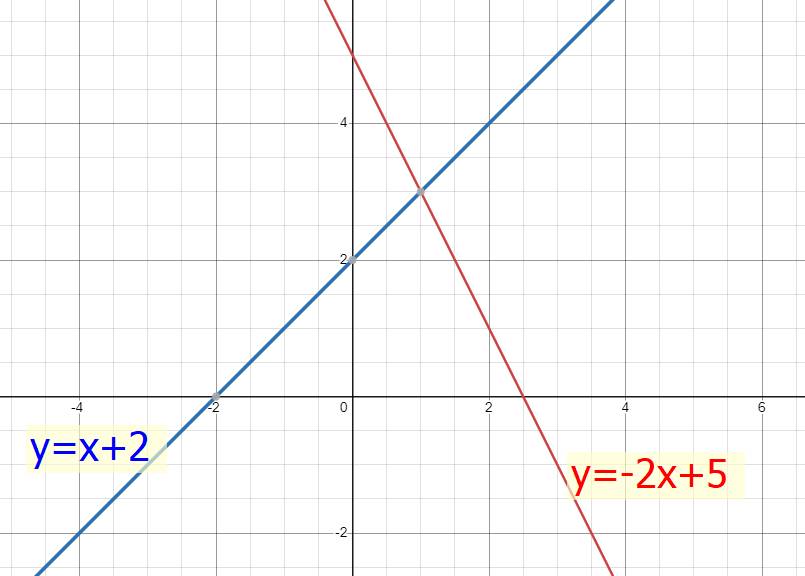
b) Ta có pt hoành độ giao điểm của (d₁) và (d₂): 

\(-2x+5=x+2\)

\(\Leftrightarrow x+2x=5-2\)

\(\Leftrightarrow3x=3\)

\(\Leftrightarrow x=1\)

Thay `x=1` vào `(d_2)` ta có: \(y=1+2=3\)

`=>M(1;3)` 

c) Hàm số `y=ax+b` có đồ thị song song với `(d_1):y=-2x+5` 

`=>a=-2` 

`=>y=-2x+b` 

Mà hàm số này đi qua điểm `K(-4;2)` ta thay `x=-4` và `y=2` vào ta có:

`2=-2*(-4)+b`

`<=>2=8+b`

`<=>b=2-8=-6` 

Vậy hàm số đó là: `y=-2x-6` 

ĐKXĐ: x ≠ 1; x ≠ -1

4/(x - 1) - A = 8/(x² - 1)

⇒ A = 4/(x - 1) - 8/(x² - 1)

= 4(x + 1)/(x² - 1) - 8/(x² - 1)

= (4x + 4 - 8)/(x² - 1)

= (4x - 4)/(x² - 1)

= 4(x - 1)/[(x - 1)(x + 1)]

= 4/(x + 1)

mình đang cần gấp

a: Xét ΔAFB và ΔCFI có

\(\widehat{FAB}=\widehat{FCI}\)(hai góc so le trong, AB//CI)

\(\widehat{AFB}=\widehat{CFI}\)(hai góc đối đỉnh)

Do đó: ΔAFB~ΔCFI

b: Xét ΔEAB và ΔEKD có

\(\widehat{EAB}=\widehat{EKD}\)(hai góc so le trong, AB//KD)

\(\widehat{AEB}=\widehat{KED}\)(hai góc đối đỉnh)

Do đó: ΔEAB~ΔEKD

=>\(\dfrac{AB}{KD}=\dfrac{AE}{KE}\)

=>\(AB\cdot KE=AE\cdot KD\)