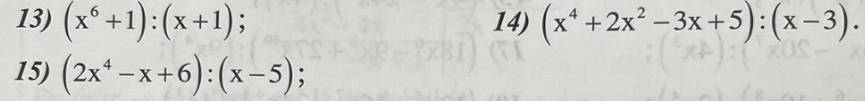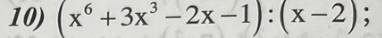Cho tam giác ABC(AB <AC) I là giao điểm của các đường phân giác trong tam giác ABC. Tia phân giác ngoài tại đỉnh B cắt AI tại J. Gọi giao điểm của AI và BC là D. a) Chứng minh 1/ai+1/aj+1/ad b) Kẻ AH vuông góc BC. Chứng minh Hc là phân giác của góc IHJ c) Kẻ Ik vuông góc BC. Chứng minh JK đi qua trung điểm AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔAFC
b: Ta có: ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{EAF}\) chung
Do đó: ΔAEF~ΔABC
=>\(\widehat{AFE}=\widehat{ACB}\)
c: Gọi O là trung điểm của AK
Ta có: BICK là hình bình hành
=>BI//CK và BK//CI
ta có: BI//CK
BI\(\perp\)AC
Do đó: CK\(\perp\)CA
=>ΔCKA vuông tại C
=>C nằm trên đường tròn đường kính AK
=>C nằm trên (O)(1)
Ta có: CI//BK
CI\(\perp\)BA
Do đó: BK\(\perp\)BA
=>ΔBKA vuông tại B
=>B nằm trên đường tròn đường kính AK
=>B nằm trên (O)(2)
Từ (1),(2) suy ra ABKC là tứ giác nội tiếp đường tròn (O), đường kính AK
Gọi H là giao điểm của AI với BC
Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại I
Do đó: I là trực tâm của ΔABC
=>AI\(\perp\)BC tại H
Xét (O) có
\(\widehat{CBK}\) là góc nội tiếp chắn cung CK
\(\widehat{CAK}\) là góc nội tiếp chắn cung CK
Do đó: \(\widehat{CBK}=\widehat{CAK}\)
mà \(\widehat{CBK}=\widehat{ICB}\)(hai góc so le trong, IC//BK)
và \(\widehat{ICB}=\widehat{FAI}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{FAI}=\widehat{CAK}\)
Xét ΔFAI vuông tại F và ΔCAK vuông tại C có
\(\widehat{FAI}=\widehat{CAK}\)
Do đó: ΔFAI~ΔCAK
=>\(\dfrac{FA}{CA}=\dfrac{FI}{CK}\)
=>\(\dfrac{FA}{FI}=\dfrac{CA}{CK}\)
=>\(\dfrac{FI}{FA}=\dfrac{CK}{CA}\)

c: Ta có: KD=KA
mà ΔAKD vuông tại K
nên ΔAKD vuông cân tại K
=>\(\widehat{KAD}=\widehat{KDA}=45^0\)
Ta có: ED//AK
AK\(\perp\)BC
Do đó: ED\(\perp\)BC
Xét tứ giác AEDB có \(\widehat{EAB}+\widehat{EDB}=90^0+90^0=180^0\)
nên AEDB là tứ giác nội tiếp
=>\(\widehat{ADB}=\widehat{AEB}\)
=>\(\widehat{AEB}=45^0\)
Xét ΔAEB vuông tại A có \(\widehat{AEB}=45^0\)
nên ΔAEB vuông cân tại A
=>AE=AB

13: \(\dfrac{x^6+1}{x+1}\)
\(=\dfrac{x^6+x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x-x-1+2}{x+1}\)
\(=x^5-x^4+x^3-x^2+x-1+\dfrac{2}{x+1}\)
14: \(\dfrac{x^4+2x^2-3x+5}{x-3}\)
\(=\dfrac{x^4-3x^3+3x^3-9x^2+11x^2-33x+30x-90+95}{x-3}\)
\(=x^3+3x^2+11x+30+\dfrac{95}{x-3}\)
15: \(\dfrac{2x^4-x+6}{x-5}\)
\(=\dfrac{2x^4-10x^3+10x^3-50x^2+50x^2-250x+249x-1245+1251}{x-5}\)
\(=2x^3+10x^2+50x+249+\dfrac{1251}{x-5}\)

1: Thay x=4 vào A, ta được:
\(A=\dfrac{4-10}{4-2}=\dfrac{-6}{2}=-3\)
2: \(B=\dfrac{x}{x-2}+\dfrac{2}{x+2}+\dfrac{8}{x^2-4}\)
\(=\dfrac{x}{x-2}+\dfrac{2}{x+2}+\dfrac{8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x+2\right)+2\left(x-2\right)+8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x+2x-4+8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)
3: P=A+B
\(=\dfrac{x+2}{x-2}+\dfrac{x-10}{x-2}=\dfrac{2x-8}{x-2}\)
Để P nguyên thì \(2x-8⋮x-2\)
=>\(2x-4-4⋮x-2\)
=>\(-4⋮x-2\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{3;1;4;0;6\right\}\)

1: Vận tốc của xe máy lúc về từ B đến A là x+10(km/h)
2: Thời gian lúc đi là \(\dfrac{60}{x}\left(giờ\right)\)
Thời gian lúc về là \(\dfrac{60}{x+10}\left(giờ\right)\)
Tổng thời gian cả đi và về (tính cả thời gian nghỉ) là:
\(\dfrac{60}{x}+\dfrac{60}{x+10}+\dfrac{1}{2}=\dfrac{60x+600+60x}{x\left(x+10\right)}+\dfrac{1}{2}\)
\(=\dfrac{120x+600}{x\left(x+10\right)}+\dfrac{1}{2}\)
\(=\dfrac{2\left(120x+600\right)+x^2+10x}{2x\left(x+10\right)}\)
\(=\dfrac{x^2+250x+1200}{2x\left(x+10\right)}\)
3: Tổng thời gian cả đi lẫn về, nghỉ là:
\(\dfrac{30^2+250\cdot30+1200}{2\cdot30\left(30+10\right)}=4\left(giờ\right)\)
=>Người đó trở lại A lúc 7h+4h=11h

\(\dfrac{x^6+3x^3-2x-1}{x-2}\)
\(=\dfrac{x^6-2x^5+2x^5-4x^4+4x^4-8x^3+11x^3-22x^2+22x^2-44x+42x-84+83}{x-2}\)
\(=\dfrac{x^5\left(x-2\right)+2x^4\left(x-2\right)+4x^3\left(x-2\right)+11x^2\left(x-2\right)+22x\left(x-2\right)+42\left(x-2\right)+83}{x-2}\)
\(=x^5+2x^4+4x^3+11x^2+22x+42+\dfrac{83}{x-2}\)

1: Xét ΔCFE vuông tại F và ΔCAB vuông tại A có
\(\widehat{FCE}\) chung
Do đó: ΔCFE~ΔCAB
=>\(\dfrac{CF}{CA}=\dfrac{CE}{CB}\)
=>\(\dfrac{CF}{CE}=\dfrac{CA}{CB}\)
=>\(CF\cdot CB=CA\cdot CE\)
2: Xét ΔCFA và ΔCEB có
\(\dfrac{CE}{CE}=\dfrac{CA}{CB}\)
\(\widehat{FCA}\) chung
Do đó: ΔCFA~ΔCEB
=>\(\widehat{CAF}=\widehat{CBE}\)
3: Xét ΔEHA vuông tại H và ΔEAB vuông tại A có
\(\widehat{HEA}\) chung
Do đó: ΔEHA~ΔEAB
=>\(\dfrac{EH}{EA}=\dfrac{EA}{EB}\)
=>\(EA^2=EH\cdot EB\)
mà EA=EC
nên \(CE^2=EH\cdot EB\)

Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)
=>\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos45=\dfrac{\sqrt{2}\cdot AB\cdot AC}{AB+AC}\)
=>\(\dfrac{AD}{\sqrt{2}}=\dfrac{AB\cdot AC}{AB+AC}\)
=>\(\dfrac{\sqrt{2}}{AD}=\dfrac{AB+AC}{AB\cdot AC}=\dfrac{1}{AB}+\dfrac{1}{AC}\)
=>Không có câu nào đúng


Gọi T là giao điểm của MN và AC. Qua K kẻ đường thẳng song song với AH cắt BC tại S và cắt AN tại R.
Ta dễ dàng chứng minh 3 cặp tam giác bằng nhau:
\(\Delta IAM=\Delta IAK,\Delta IBM=\Delta IBN,\Delta ICN=\Delta ICK\)
\(\Rightarrow AM=AK,BM=BN,CN=CK\)
\(\Rightarrow\dfrac{MA}{MB}.\dfrac{NB}{NC}.\dfrac{KC}{KA}=1\)
Áp dụng định lý Menelaus cho tam giác ABC, cát tuyến MNT, ta có:
\(\dfrac{MA}{MB}.\dfrac{NB}{NC}.\dfrac{TC}{TA}=1\)
Do đó \(\dfrac{KC}{KA}=\dfrac{TC}{TA}\) \(\Rightarrow\dfrac{TA}{KA}=\dfrac{TC}{KC}\) (1)
Áp dụng định lý Thales trong tam giác ANT, ta có:
\(\dfrac{TA}{KA}=\dfrac{TN}{RK}\) (2)
Áp dụng định lý Thales trong tam giác CNT, ta có:
\(\dfrac{TC}{KC}=\dfrac{TN}{KS}\) (3)
Từ (1), (2) và (3), suy ra \(RK=KS\) (4)
Áp dụng định lý Thales cho tam giác NKR, ta có:
\(\dfrac{AE}{RK}=\dfrac{NE}{NK}\) (5)
Áp dụng định lý Thales cho tam giác NKS, ta có:
\(\dfrac{EH}{SK}=\dfrac{NE}{NK}\) (6)
Từ (4), (5) và (6), suy ra \(AE=EH\) \(\Rightarrow\) E là trung điểm AH.
CMTT \(\Rightarrow\) DE là đường trung bình của tam giác AQH (đpcm)