
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: Ta có: KD=KA
mà ΔAKD vuông tại K
nên ΔAKD vuông cân tại K
=>\(\widehat{KAD}=\widehat{KDA}=45^0\)
Ta có: ED//AK
AK\(\perp\)BC
Do đó: ED\(\perp\)BC
Xét tứ giác AEDB có \(\widehat{EAB}+\widehat{EDB}=90^0+90^0=180^0\)
nên AEDB là tứ giác nội tiếp
=>\(\widehat{ADB}=\widehat{AEB}\)
=>\(\widehat{AEB}=45^0\)
Xét ΔAEB vuông tại A có \(\widehat{AEB}=45^0\)
nên ΔAEB vuông cân tại A
=>AE=AB

13: \(\dfrac{x^6+1}{x+1}\)
\(=\dfrac{x^6+x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2+x-x-1+2}{x+1}\)
\(=x^5-x^4+x^3-x^2+x-1+\dfrac{2}{x+1}\)
14: \(\dfrac{x^4+2x^2-3x+5}{x-3}\)
\(=\dfrac{x^4-3x^3+3x^3-9x^2+11x^2-33x+30x-90+95}{x-3}\)
\(=x^3+3x^2+11x+30+\dfrac{95}{x-3}\)
15: \(\dfrac{2x^4-x+6}{x-5}\)
\(=\dfrac{2x^4-10x^3+10x^3-50x^2+50x^2-250x+249x-1245+1251}{x-5}\)
\(=2x^3+10x^2+50x+249+\dfrac{1251}{x-5}\)

1: Thay x=4 vào A, ta được:
\(A=\dfrac{4-10}{4-2}=\dfrac{-6}{2}=-3\)
2: \(B=\dfrac{x}{x-2}+\dfrac{2}{x+2}+\dfrac{8}{x^2-4}\)
\(=\dfrac{x}{x-2}+\dfrac{2}{x+2}+\dfrac{8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x+2\right)+2\left(x-2\right)+8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x+2x-4+8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)
3: P=A+B
\(=\dfrac{x+2}{x-2}+\dfrac{x-10}{x-2}=\dfrac{2x-8}{x-2}\)
Để P nguyên thì \(2x-8⋮x-2\)
=>\(2x-4-4⋮x-2\)
=>\(-4⋮x-2\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{3;1;4;0;6\right\}\)

1: Vận tốc của xe máy lúc về từ B đến A là x+10(km/h)
2: Thời gian lúc đi là \(\dfrac{60}{x}\left(giờ\right)\)
Thời gian lúc về là \(\dfrac{60}{x+10}\left(giờ\right)\)
Tổng thời gian cả đi và về (tính cả thời gian nghỉ) là:
\(\dfrac{60}{x}+\dfrac{60}{x+10}+\dfrac{1}{2}=\dfrac{60x+600+60x}{x\left(x+10\right)}+\dfrac{1}{2}\)
\(=\dfrac{120x+600}{x\left(x+10\right)}+\dfrac{1}{2}\)
\(=\dfrac{2\left(120x+600\right)+x^2+10x}{2x\left(x+10\right)}\)
\(=\dfrac{x^2+250x+1200}{2x\left(x+10\right)}\)
3: Tổng thời gian cả đi lẫn về, nghỉ là:
\(\dfrac{30^2+250\cdot30+1200}{2\cdot30\left(30+10\right)}=4\left(giờ\right)\)
=>Người đó trở lại A lúc 7h+4h=11h

\(\dfrac{x^6+3x^3-2x-1}{x-2}\)
\(=\dfrac{x^6-2x^5+2x^5-4x^4+4x^4-8x^3+11x^3-22x^2+22x^2-44x+42x-84+83}{x-2}\)
\(=\dfrac{x^5\left(x-2\right)+2x^4\left(x-2\right)+4x^3\left(x-2\right)+11x^2\left(x-2\right)+22x\left(x-2\right)+42\left(x-2\right)+83}{x-2}\)
\(=x^5+2x^4+4x^3+11x^2+22x+42+\dfrac{83}{x-2}\)

1: Xét ΔCFE vuông tại F và ΔCAB vuông tại A có
\(\widehat{FCE}\) chung
Do đó: ΔCFE~ΔCAB
=>\(\dfrac{CF}{CA}=\dfrac{CE}{CB}\)
=>\(\dfrac{CF}{CE}=\dfrac{CA}{CB}\)
=>\(CF\cdot CB=CA\cdot CE\)
2: Xét ΔCFA và ΔCEB có
\(\dfrac{CE}{CE}=\dfrac{CA}{CB}\)
\(\widehat{FCA}\) chung
Do đó: ΔCFA~ΔCEB
=>\(\widehat{CAF}=\widehat{CBE}\)
3: Xét ΔEHA vuông tại H và ΔEAB vuông tại A có
\(\widehat{HEA}\) chung
Do đó: ΔEHA~ΔEAB
=>\(\dfrac{EH}{EA}=\dfrac{EA}{EB}\)
=>\(EA^2=EH\cdot EB\)
mà EA=EC
nên \(CE^2=EH\cdot EB\)

Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)
=>\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos45=\dfrac{\sqrt{2}\cdot AB\cdot AC}{AB+AC}\)
=>\(\dfrac{AD}{\sqrt{2}}=\dfrac{AB\cdot AC}{AB+AC}\)
=>\(\dfrac{\sqrt{2}}{AD}=\dfrac{AB+AC}{AB\cdot AC}=\dfrac{1}{AB}+\dfrac{1}{AC}\)
=>Không có câu nào đúng


Gọi T là giao điểm của MN và AC. Qua K kẻ đường thẳng song song với AH cắt BC tại S và cắt AN tại R.
Ta dễ dàng chứng minh 3 cặp tam giác bằng nhau:
\(\Delta IAM=\Delta IAK,\Delta IBM=\Delta IBN,\Delta ICN=\Delta ICK\)
\(\Rightarrow AM=AK,BM=BN,CN=CK\)
\(\Rightarrow\dfrac{MA}{MB}.\dfrac{NB}{NC}.\dfrac{KC}{KA}=1\)
Áp dụng định lý Menelaus cho tam giác ABC, cát tuyến MNT, ta có:
\(\dfrac{MA}{MB}.\dfrac{NB}{NC}.\dfrac{TC}{TA}=1\)
Do đó \(\dfrac{KC}{KA}=\dfrac{TC}{TA}\) \(\Rightarrow\dfrac{TA}{KA}=\dfrac{TC}{KC}\) (1)
Áp dụng định lý Thales trong tam giác ANT, ta có:
\(\dfrac{TA}{KA}=\dfrac{TN}{RK}\) (2)
Áp dụng định lý Thales trong tam giác CNT, ta có:
\(\dfrac{TC}{KC}=\dfrac{TN}{KS}\) (3)
Từ (1), (2) và (3), suy ra \(RK=KS\) (4)
Áp dụng định lý Thales cho tam giác NKR, ta có:
\(\dfrac{AE}{RK}=\dfrac{NE}{NK}\) (5)
Áp dụng định lý Thales cho tam giác NKS, ta có:
\(\dfrac{EH}{SK}=\dfrac{NE}{NK}\) (6)
Từ (4), (5) và (6), suy ra \(AE=EH\) \(\Rightarrow\) E là trung điểm AH.
CMTT \(\Rightarrow\) DE là đường trung bình của tam giác AQH (đpcm)

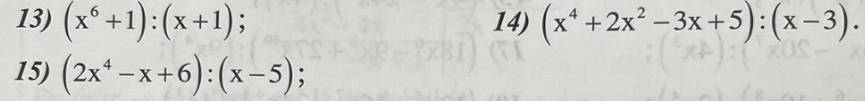


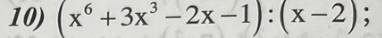


a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔAFC
b: Ta có: ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{EAF}\) chung
Do đó: ΔAEF~ΔABC
=>\(\widehat{AFE}=\widehat{ACB}\)
c: Gọi O là trung điểm của AK
Ta có: BICK là hình bình hành
=>BI//CK và BK//CI
ta có: BI//CK
BI\(\perp\)AC
Do đó: CK\(\perp\)CA
=>ΔCKA vuông tại C
=>C nằm trên đường tròn đường kính AK
=>C nằm trên (O)(1)
Ta có: CI//BK
CI\(\perp\)BA
Do đó: BK\(\perp\)BA
=>ΔBKA vuông tại B
=>B nằm trên đường tròn đường kính AK
=>B nằm trên (O)(2)
Từ (1),(2) suy ra ABKC là tứ giác nội tiếp đường tròn (O), đường kính AK
Gọi H là giao điểm của AI với BC
Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại I
Do đó: I là trực tâm của ΔABC
=>AI\(\perp\)BC tại H
Xét (O) có
\(\widehat{CBK}\) là góc nội tiếp chắn cung CK
\(\widehat{CAK}\) là góc nội tiếp chắn cung CK
Do đó: \(\widehat{CBK}=\widehat{CAK}\)
mà \(\widehat{CBK}=\widehat{ICB}\)(hai góc so le trong, IC//BK)
và \(\widehat{ICB}=\widehat{FAI}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{FAI}=\widehat{CAK}\)
Xét ΔFAI vuông tại F và ΔCAK vuông tại C có
\(\widehat{FAI}=\widehat{CAK}\)
Do đó: ΔFAI~ΔCAK
=>\(\dfrac{FA}{CA}=\dfrac{FI}{CK}\)
=>\(\dfrac{FA}{FI}=\dfrac{CA}{CK}\)
=>\(\dfrac{FI}{FA}=\dfrac{CK}{CA}\)