Cho nửa đường tròn (o,r) đường kính AB. Trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn (o,r) vẽ các tiếp tuyến ax, by với nửa đường tròn. Gọi M là một điểm bất kì trên nửa đường tròn (O,R), tiếp tuyến của nửa đường tròn tại M cắt Ax, By lần lượt tại C và D. Kẻ MN vuông góc AB, BC cắt MN tại I. Chứng minh I là trung điểm MN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H9
HT.Phong (9A5)
CTVHS
24 tháng 1 2024
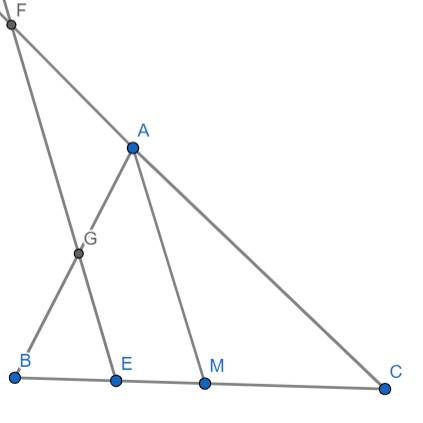
Ta có: \(EF//AM\left(gt\right)\)
\(\Rightarrow\widehat{FEC}=\widehat{AMC}\) (đồng vị)
Xét hai tam giác FEC và AMC có:
\(\widehat{FCE}\) chung
\(\widehat{FEC}=\widehat{AMC}\) (cmt)
\(\Rightarrow\Delta FEC\sim\Delta AMC\) (g.g)
\(\Rightarrow\dfrac{EF}{AM}=\dfrac{CE}{CM}\Rightarrow\dfrac{CM}{AM}=\dfrac{CE}{EF}\) (1)
Chứng minh tương tự ta có: \(\Delta BEG\sim\Delta BMA\left(g.g\right)\)
\(\Rightarrow\dfrac{EG}{AM}=\dfrac{BE}{BM}\Rightarrow\dfrac{CM}{AM}=\dfrac{BE}{EG}\) (vì \(CM=BM\)) (2)
Từ (1) và (2) ta có:
\(\dfrac{CE}{EF}=\dfrac{BE}{EG}\Rightarrow EG\cdot CE=EF\cdot BE\)
\(\Rightarrow EG\cdot\left(BC-BE\right)=EF\cdot BE\)
\(\Rightarrow EG\cdot BC-EG\cdot BE=EF\cdot BE\)
\(\Rightarrow EF\cdot BE+EG\cdot BE=EG\cdot BC\)
\(\Rightarrow EF+EG=\dfrac{EG\cdot BC}{BE}\left(3\right)\)
Từ (2) ta có: \(\dfrac{EG}{AM}=\dfrac{BE}{BM}\)
\(\Rightarrow BM\cdot EG=BE\cdot AM\Rightarrow\dfrac{1}{2}BC\cdot EG=BE\cdot AM\)
\(\Rightarrow EG\cdot BC=2AM\cdot BE\)
\(\Rightarrow2AM=\dfrac{EG\cdot BC}{BE}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow EF+EG=2AM\) (đpcm)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 1 2024
E A B C D M O N
a/
Ta có M và A cùng nhìn OC dưới 1 góc \(90^o\) => ACMO là tứ giác nội tiếp
b/
Xét tg vuông BED và tg vuông AEC có \(\widehat{BED}\) chung
=> tg BED đồng dạng với tg AEC (g.g.g)
\(\Rightarrow\dfrac{DB}{CA}=\dfrac{DE}{CE}\)
Mà
\(DB=DM;CA=CM\) (Hai tiếp tuyến cùng xp từ 1 điểm...)\(\Rightarrow\dfrac{DB}{CA}=\dfrac{DM}{CM}=\dfrac{DE}{CE}\Rightarrow DM.CE=CM.DE\)
c/
Ta có
\(CA\perp AB\left(gt\right);DB\perp AB\left(gt\right)\) => CA//DB
\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DB}{CA}\) (Talet)
Mà \(\dfrac{DM}{CM}=\dfrac{DB}{CA}\left(cmt\right)\)
\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DM}{CM}\) => MN//BD (Talet đảo trong tam giác)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 1 2024
A B H K C E I M
Xét \(\Delta ABE\) có
\(AE=AB\Rightarrow\Delta ABE\) cân tại A
Ta có \(MB=ME\left(gt\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{EAM}=\dfrac{\widehat{BAC}}{2}=\dfrac{90^o}{2}=45^o\) và \(AM\perp BE\)(Trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao và đường phân giác của góc ở đỉnh tg cân)
Ta có M và H cùng nhìn AB dưới một góc \(90^o\) => ABHM là tứ giác nội tiếp
\(\Rightarrow\widehat{ABE}=\widehat{AHM}=45^o\) (góc nt cùng chắn cung AM)
\(\Rightarrow\widehat{CHM}=\widehat{AHC}-\widehat{AHM}=90^o-45^o=45^o\)
\(\Rightarrow\widehat{AHM}=\widehat{CHM}=45^o\) => HM là phân giác của \(\widehat{AHC}\)