Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>PA\(\perp\)BD tại A
Xét tứ giác ACHD có \(\widehat{CHD}+\widehat{CAD}=90^0+90^0=180^0\)
nên ACHD là tứ giác nội tiếp đường tròn đường kính CD
Tâm là trung điểm của CD
b: Xét ΔPHC vuông tại H và ΔPAD vuông tại A có
\(\widehat{HPC}\) chung
Do đó: ΔPHC~ΔPAD
=>\(\dfrac{PH}{PA}=\dfrac{PC}{PD}\)
=>\(PH\cdot PD=PA\cdot PC\)
c: Xét (O) có
ΔCIB nội tiếp
BC là đường kính
Do đó: ΔCIB vuông tại I
=>CI\(\perp\)BP tại I
Xét ΔBDP có
BH,PA là các đường cao
BH cắt PA tại C
Do đó: C là trực tâm của ΔBDP
=>DC\(\perp\)BP
mà CI\(\perp\)BP
và DC,CI có điểm chung là C
nên D,C,I thẳng hàng

ĐKXĐ: x<>0 và y<>0
\(\left\{{}\begin{matrix}\dfrac{210}{x}-\dfrac{210}{y}=\dfrac{7}{4}\\4x+\dfrac{9}{4}y=210\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{30}{x}-\dfrac{30}{y}=\dfrac{1}{4}\\16x+9y=840\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}30\left(\dfrac{1}{x}-\dfrac{1}{y}\right)=\dfrac{1}{4}\\16x=840-9y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{120}\\x=\dfrac{840-9y}{16}\end{matrix}\right.\)
\(\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{120}\)
=>\(\dfrac{16}{840-9y}-\dfrac{1}{y}=\dfrac{1}{120}\)
=>\(\dfrac{16y-840+9y}{y\left(840-9y\right)}=\dfrac{1}{120}\)
=>\(y\left(840-9y\right)=120\left(25y-840\right)\)
=>\(-9y^2+840y-3000y+100800=0\)
=>\(-9y^2-2160y+100800=0\)
=>\(y^2+240y-11200=0\)
=>\(\left[{}\begin{matrix}y=40\left(nhận\right)\\y=-280\left(nhận\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{840-9\cdot40}{16}=\dfrac{840-360}{16}=30\left(nhận\right)\\x=\dfrac{840-9\cdot\left(-280\right)}{16}=210\left(nhận\right)\end{matrix}\right.\)

a: Theo Vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=2;x_1x_2=-4\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=2^2-2\cdot\left(-4\right)=4+8=12\)
b: \(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=2^2-4\cdot\left(-4\right)=20\)
=>\(x_1-x_2=\pm2\sqrt{5}\)
c: \(\left|x_1^2-x_2^2\right|\)
\(=\left|\left(x_1-x_2\right)\left(x_1+x_2\right)\right|\)
\(=\left|2\sqrt{5}\cdot2\right|=4\sqrt{5}\)
d: \(x_1^3\cdot x_2+x_1\cdot x_2^3\)
\(=x_1x_2\left(x_1^2+x_2^2\right)\)
\(=-4\cdot12=-48\)

\(x_1+x_2=-\dfrac{b}{a}=-5;x_1x_2=2\)
\(x_1^2\cdot x_2^3+x_2^2\cdot x_1^3\)
\(=\left(x_1x_2\right)^2\cdot\left(x_1+x_2\right)\)
\(=2^2\cdot\left(-5\right)=-20\)

Pt: \(x^2+5x+2=0\)
Theo vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-5}{1}=-5\\x_1x_2=\dfrac{2}{1}=2\end{matrix}\right.\)
a) \(x^2_1+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-5\right)^2-2\cdot2=25-4=21\)
b) \(x_1^3+x_2^3=\left(x_1+x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\right]\)
\(=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-3x_1x_2\right]=\left(-5\right)\cdot\left[\left(-5\right)^2-3\cdot2\right]=-95\)
c) \(\left|x_1-x_2\right|=\sqrt{\left|x_1-x_2\right|^2}=\sqrt{x_1^2+x_2^2-2\left|x_1x_2\right|}\)
\(=\sqrt{\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|}=\sqrt{\left(-5\right)^2-2\cdot2-2\cdot\left|2\right|}=\sqrt{17}\)
d) \(x_1^2x_2^3+x_2^2x_1^3=x_1^2x_2^2\left(x_1+x_2\right)=\left(x_1x_2\right)^2\cdot\left(x_1+x_2\right)=2^2\cdot\left(-5\right)=-20\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=2\end{matrix}\right.\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-5\right)^2-2.2=21\)
\(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\left(-5\right)^3-3.2.\left(-5\right)=-95\)
\(\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{\left(-5\right)^2-4.2}=\sqrt{17}\)
\(x_1^2x_2^3+x_1^3x_2^2=\left(x_1x_2\right)^2\left(x_1+x_2\right)=2^2.\left(-5\right)=-20\)

a:
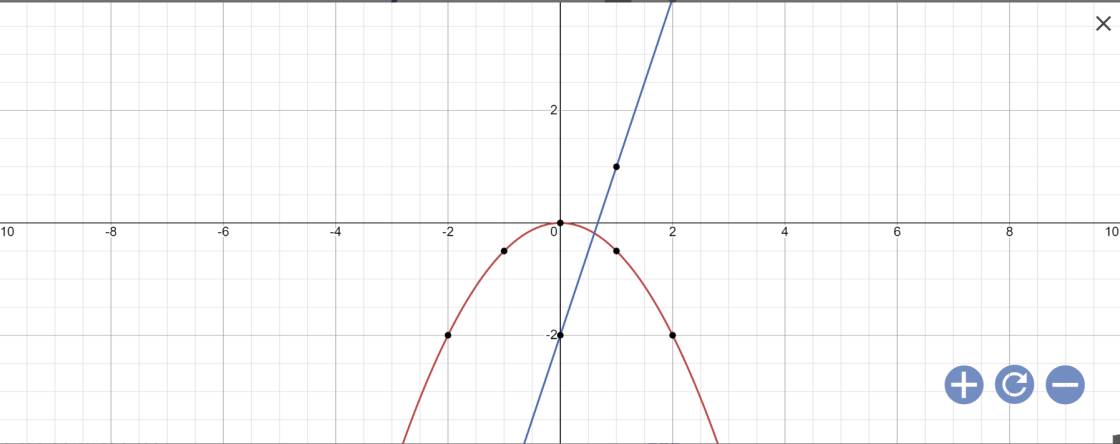
Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x^2=3x-2\)
=>\(-x^2=6x-4\)
=>\(x^2+6x-4=0\)
=>\(\left(x+3\right)^2-13=0\)
=>\(\left(x+3\right)^2=13\)
=>\(\left[{}\begin{matrix}x+3=\sqrt{13}\\x+3=-\sqrt{13}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{13}-3\\x=-\sqrt{13}-3\end{matrix}\right.\)
Thay \(x=\sqrt{13}-3\) vào y=3x-2, ta được:
\(y=3\left(\sqrt{13}-3\right)-2=3\sqrt{13}-11\)
Thay \(x=-\sqrt{13}-3\) vào y=3x-2, ta được:
\(y=3\left(-\sqrt{13}-3\right)-2=-3\sqrt{13}-11\)
Vậy: (P) cắt (d) tại \(C\left(\sqrt{13}-3;3\sqrt{13}-11\right);D\left(-\sqrt{13}-3;-3\sqrt{13}-11\right)\)
b: Thay x=-4 vào (P), ta được:
\(y=-\dfrac{1}{2}\cdot\left(-4\right)^2=-\dfrac{1}{2}\cdot16=-8\)
Vậy: A(3;1); B(-4;-8)
Thay x=3 và y=1 vào (d'), ta được:
\(3\cdot a+b=1\)(1)
Thay x=-4 và y=-8 vào (d'), ta được:
\(a\cdot\left(-4\right)+b=-8\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=1\\-4a+b=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7a=9\\3a+b=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{9}{7}\\b=1-3a=1-\dfrac{27}{7}=-\dfrac{20}{7}\end{matrix}\right.\)




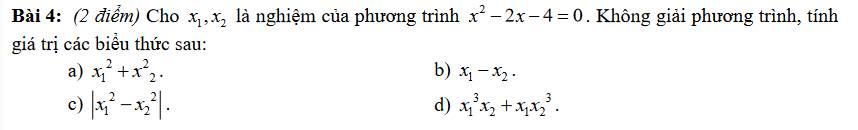

- Với cửa hàng A:
Giá bán trà sữa từ ly thứ 5 trở đi: \(25000.85\%=21250\) (đồng/ly)
An mua đúng 20 lý nên có 4 ly giá 25000 đồng và 16 ly giá 21250 đồng.
Do đó tổng số tiền phải trả nếu mua ở cửa hàng A là:
\(4.25000+16.21250=440000\) (đồng)
- Với cửa hàng B:
Khi mua 15 ly sẽ được tặng \(15:5=3\) ly, do đó An cần mua thêm 2 ly nữa để đủ 20 ly.
Do đó An cần trả tiền cho \(15+2=17\) ly trà sữa
Số tiền mua ở cửa hàng B là:
\(17.25000=425000\) (đồng)
Vậy An nên mua ở cửa hàng B để tiết kiệm hơn.
Số tiền tiết kiệm được là:
\(440000-425000=15000\) (đồng)