 giúp em 2 bài này với , em đang cần gấp ạ , em cảm ơn
giúp em 2 bài này với , em đang cần gấp ạ , em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mona Lisa:
Tác giả: Leonardo da Vinci
Thời điểm: 1503 - 1519
Nơi trưng bày: Bảo tàng Louvre, Paris, Pháp
Nổi tiếng từ: Thế kỷ 19
Màu sắc: Chủ yếu là màu nâu, vàng, đỏ và xanh lá
The Scream (Tiếng Thét):
Tác giả: Edvard Munch
Thời điểm: 1893 (bản đầu tiên), 1910 (bản sơn)
Nơi trưng bày:
Bản sơn: Phòng trưng bày Quốc gia, Oslo, Na Uy
Bản phấn màu: Bảo tàng Munch, Oslo, Na Uy
Nổi tiếng từ: Đầu thế kỷ 20
Màu sắc: Chủ yếu là màu đỏ, cam, vàng và xanh lam
Lưu ý:
Mona Lisa được vẽ bằng sơn dầu trên gỗ dương.
The Scream có 4 phiên bản: 2 bản vẽ bằng phấn màu và 2 bản vẽ bằng sơn.
Cả hai bức tranh đều được coi là những tác phẩm nghệ thuật biểu tượng và có giá trị cao.

Gọi thời gian làm riêng 1 mình xong việc của tổ 1 và tổ 2 lần lượt là x và y giờ (với x;y>0)
Trong 1h tổ 1 làm được \(\dfrac{1}{x}\) phần công việc và tổ 2 làm được \(\dfrac{1}{y}\) phần công việc
Do 2 tổ làm chung trong 12 giờ thì xong việc nên:
\(12\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\) (1)
2 tổ làm chung trong 3 giờ được: \(3\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=\dfrac{3}{x}+\dfrac{3}{y}\) phần việc
Tô2 1 làm trong 7 giờ được: \(\dfrac{7}{x}\) phần việc
Do 2 tổ làm chung trong 3 giờ sau đó tổ 1 làm 1 mình trong 7 giờ được 7/12 công việc nên ta có:
\(\dfrac{3}{x}+\dfrac{3}{y}+\dfrac{7}{x}=\dfrac{7}{12}\Leftrightarrow\dfrac{10}{x}+\dfrac{3}{y}=\dfrac{7}{12}\) (2)
Từ (1) và (2) ta được hệ:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{10}{x}+\dfrac{3}{y}=\dfrac{7}{12}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{21}\\\dfrac{1}{y}=\dfrac{1}{28}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=21\\y=28\end{matrix}\right.\)
+ Tổ 1 làm riêng thì sau 18 giờ sẽ hoàn thành công việc.
+ Tổ 2 làm riêng thì sau 24 giờ sẽ hoàn thành công việc.

Giải:
Gọi thời gian tổ một làm một mình xong công việc là \(x\) (giờ); \(x>0\)
Thì một giờ tổ một làm một mình được:
1 : \(x\) = \(\dfrac{1}{x}\) (công việc)
Trong một giờ cả hai tổ cùng làm được:
1 : \(\dfrac{1}{12}\) (công việc)
Tổ hai làm một mình trong một giờ được:
\(\dfrac{1}{12}\) - \(\dfrac{1}{x}\) (công việc)
Trong 7 giờ tổ 1 làm được:
\(\dfrac{1}{x}\) x 7 = \(\dfrac{7}{x}\) (công việc)
Theo bài ra ta có:
\(\dfrac{1}{12}\) x 3 + \(\dfrac{7}{x}\) = \(\dfrac{7}{12}\)
\(\dfrac{7}{x}\) = \(\dfrac{7}{12}\) - \(\dfrac{1}{4}\)
\(\dfrac{7}{x}\) = \(\dfrac{1}{3}\)
\(x\) = 7 : \(\dfrac{1}{3}\)
\(x=21\)
Vậy đội một làm xong công việc trong 21 giờ nếu làm một mình
Nếu làm một mình, đội hai làm xong công việc trong:
1: (\(\dfrac{1}{12}-\dfrac{1}{21}\)) = 28 (giờ)
Kết luận:...

a. Em tự giải
b.
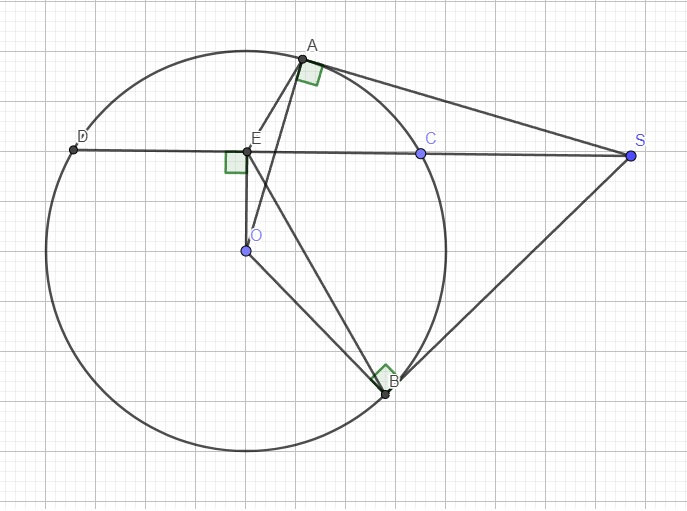
Từ câu a ta có SAOB nội tiếp
Mà \(SA=SB\) (t/c hai tiếp tuyến cắt nhau)
\(\Rightarrow\widehat{SEA}=\widehat{SEB}\) (hai góc nt chắn 2 cùng bằng nhau của đường tròn ngoại tiếp SAOB)
\(\Rightarrow\widehat{AEB}=2\widehat{SEB}\) (1)
Do E là trung điểm CD \(\Rightarrow SE\perp CD\)
\(\Rightarrow E,A,B\) cùng nhìn SO dưới 1 góc vuông nên S,A,E,B,O cùng thuộc 1 đường tròn
Hay SAEB nội tiếp
\(\Rightarrow\widehat{AEB}+\widehat{ASB}=180^0\)
Theo câu a SAOB nội tiếp \(\Rightarrow\widehat{AOB}+\widehat{ASB}=180^0\)
\(\Rightarrow\widehat{AEB}=\widehat{AOB}\) (2)
(1);(2) \(\Rightarrow\widehat{AOB}=2\widehat{SEB}\)

Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R) có 2 đường cao BE và CF cắt nhau tại H, AH cắt (O) tại K. Gọi I là trung điểm cạnh AH. Lấy điểm M thuộc cạnh KC, điểm N thuộc cạnh ME sao cho HM // BK và HN // BC. Gọi P và Q lần lượt là trung điểm các cạnh NI và NK, PE cắt MQ tại L. Đường thẳng qua L song song với AK cắt BK và SI lần lượt tại S và T. Chứng minh : Nếu $\tan B \cdot \tan C = 3$ thì L là trung điểm cạnh ST (B,C là góc tam giác ABC).


a) Tứ giác BNMC có:
\(\widehat{BNC}=\widehat{BMC}=90^0\) (do BM và CN là hai đường cao của \(\Delta ABC\))
\(\Rightarrow M,N\) cùng nhìn BC dưới một góc \(90^0\)
\(\Rightarrow BNMC\) nội tiếp
*) Gọi \(I\) là trung điểm của BC
\(\Delta BMC\) vuông tại M, có MI là đường trung tuyến ứng với cạnh huyền BC
\(\Rightarrow IM=IB=IC=\dfrac{BC}{2}\) (1)
\(\Delta BNC\) vuông tại N, có NI là đường trung tuyến ứng với cạnh huyền BC
\(\Rightarrow IN=IB=IC=\dfrac{BC}{2}\) (2)
Từ (1) và (2) \(\Rightarrow IM=IN=IB=IC=\dfrac{BC}{2}\)
Vậy \(I\) là tâm của đường tròn ngoại tiếp tứ giác BNMC
b) Do BNMC là tứ giác nội tiếp (cmt)
\(\Rightarrow\widehat{AMN}=\widehat{ABC}\) (góc ngoài tại đỉnh M bằng góc trong tại đỉnh B của tứ giác BNMC)
Xét \(\Delta AMN\) và \(\Delta ABC\) có:
\(\widehat{A}\) chung
\(\widehat{AMN}=\widehat{ABC}\) (cmt)
\(\Delta AMN\) ∽ \(\Delta ABC\) (g-g)
a: Xét tứ giác BNMC có \(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BNMC là tứ giác nội tiếp đường tròn đường kính BC
tâm I là trung điểm của BC
b: Ta có: BNMC là tứ giác nội tiếp
=>\(\widehat{BNM}+\widehat{BCM}=180^0\)
mà \(\widehat{BNM}+\widehat{ANM}=180^0\)(hai góc kề bù)
nên \(\widehat{ANM}=\widehat{ACB}\)
Xét ΔANM và ΔACB có
\(\widehat{ANM}=\widehat{ACB}\)
\(\widehat{NAM}\) chung
Do đó: ΔANM~ΔACB

Gọi số dụng cụ mỗi ngày phải làm là x(dụng cụ), gọi số ngày phải hoàn thành là y(ngày)
(Điều kiện: \(x\in Z^+;y>0\))
Người thứ nhất làm vượt mức mỗi ngày 3 dụng cụ nên làm xong công việc sớm 2 ngày nên ta có:
(x+3)(y-2)=xy
=>xy-2x+3y-6=xy
=>-2x+3y=6(1)
Người thứ hai làm kém định mức mỗi ngày 3 dụng cụ nên hoàn thành lâu hơn 3 ngày nên ta có:
(x-3)(y+3)=xy
=>xy+3x-3y-9=xy
=>3x-3y=9
=>x-y=3(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-2x+3y=6\\x-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+3y=6\\2x-2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x+3y+2x-2y=6+6\\x-y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=12\\x=y+3=15\end{matrix}\right.\left(nhận\right)\)
Số dụng cụ được giao là 12*15=180(dụng cụ)

a: 5-(x-6)=4(2x-3)
=>8x-12=5-x+6
=>8x-12=-x+11
=>9x=23
=>\(x=\dfrac{23}{9}\)
b: \(3-4x+24+6x=x+27+3x\)
=>\(4x+27=2x+27\)
=>2x=0
=>x=0
c: \(\left(x+5\right)\left(x-1\right)=2x\left(x-1\right)\)
=>\(2x\left(x-1\right)-\left(x+5\right)\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(2x-x-5\right)=0\)
=>(x-1)(x-5)=0
=>\(\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
d: \(5\left(3x-2\right)-4\left(5-3x\right)=1\)
=>\(15x-10-20+12x=1\)
=>27x=1+30=31
=>\(x=\dfrac{31}{27}\)

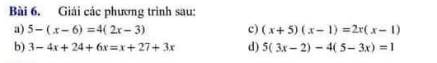
Bài 2:
a: (d) có hệ số góc là k nên (d): y=kx+b
Thay x=0 và y=-1 vào (d), ta được:
\(k\cdot0+b=-1\)
=>b=-1
Vậy: (d): y=kx-1
b: Phương trình hoành độ giao điểm là;
\(-x^2=kx-1\)
=>\(x^2+kx-1=0\)
\(a=1;b=k;c=-1\)
\(\text{Δ}=b^2-4ac=k^2-4\cdot1\cdot\left(-1\right)=k^2+4>=4>0\forall k\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
c: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-k\\x_1x_2=\dfrac{c}{a}=-1\end{matrix}\right.\)
\(\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}\)
\(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{k^2-4\cdot\left(-1\right)}\)
\(=\sqrt{k^2+4}>=\sqrt{4}=2\)