\(\hept{\begin{cases}x^4-x^3+3x^2-4y-1=0\\\sqrt{\frac{x^2+4y^2}{2}}+\sqrt{\frac{x^2+2xy+4y^2}{3}}=x+2y\end{cases}}\)giải hệ pt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(y^2+xy+x+y+5=y^2+xy+x+y+4+1\)
\(=y^2+xy+x+y+\left(x+y\right)\left(x+1\right)+1\)
\(=\left(x+y+1\right)^2\)
\(x^3+y^3+12y+13=x^3+y^3+12\left(y+1\right)+1\)
\(=x^3+y^3+3\left(x+y\right)\left(x+1\right)\left(y+1\right)+1\)
\(=x^3+y^3+3\left(x+y\right)\left(xy+x+y+1\right)+1\)
\(=x^3+y^3+3xy\left(x+y\right)+3\left(x+y\right)\left(x+y+1\right)+1\)
\(=\left(x+y+1\right)^3\)
Khi đó phương trình thứ hai tương đương với
\(\left(x+y+1\right)^5=243\Leftrightarrow x+y+1=3\)
Từ đây kết hợp phương trình một ta được \(x=y=1\).

a, Ta có \(\sqrt{25-16}=\sqrt{9}=3\)
\(\sqrt{25}-\sqrt{16}=5-4=1\)
Do 3 > 1 nên \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)
a) căn 25 - 16 > căn 25 - căn 16
b)Với nên đều xác định
Để so sánh và ta quy về so sánh và .
+) .
+)
.
Do nên
Do
(đpcm)
Vậy .

(Vì x > 0 nên |x| = x; y2 > 0 với mọi y ≠ 0)
(Vì x2 ≥ 0 với mọi x; và vì y < 0 nên |2y| = – 2y)
(Vì x < 0 nên |5x| = – 5x; y > 0 nên |y3| = y3)
(Vì x2y4 = (xy2)2 > 0 với mọi x ≠ 0, y ≠ 0)

a, \(\frac{\sqrt{2}}{\sqrt{18}}=\sqrt{\frac{2}{18}}=\sqrt{\frac{1}{9}}=\frac{1}{3}\)
b, \(\frac{\sqrt{15}}{\sqrt{735}}=\sqrt{\frac{15}{735}}=\sqrt{\frac{1}{49}}=\frac{1}{7}\)
c, \(\frac{\sqrt{12500}}{\sqrt{500}}=\sqrt{\frac{12500}{500}}=\sqrt{\frac{125}{5}}=\sqrt{25}=5\)
d, \(\frac{\sqrt{6^5}}{\sqrt{2^3.3^5}}=\sqrt{\frac{6^5}{2^3.3^5}}=\sqrt{\frac{2^5.3^5}{2^3.3^5}}=\sqrt{2^2}=2\)
a) căn 2 / căn 18 = 1/3
b) căn 15/ căn 735 = 1/7
c) căn 12500 / căn 500 = 5
d) căn 6^5 / 2^3 * 3^5 = 2

a, \(\sqrt{\frac{289}{25}}=\frac{\sqrt{289}}{\sqrt{25}}=\frac{17}{5}\)
b, \(\sqrt{2\frac{14}{25}}=\sqrt{\frac{64}{25}}=\frac{8}{5}\)
c, \(\sqrt{\frac{0,25}{9}}=\frac{\sqrt{0,25}}{\sqrt{9}}=\frac{0,5}{3}=\frac{1}{2}.\frac{1}{3}=\frac{1}{6}\)
d, \(\sqrt{\frac{8,1}{16}}\)đề có sai ko cô ?
a) căn 289 / 225 = 17/15
b) căn 64/ 25 = 8/5
c) căn 0,25 / 9 = 1/6
d) căn 8,1 / 1,6 = 9/4

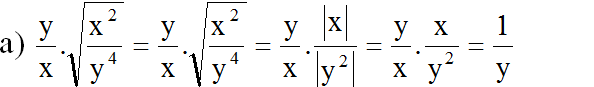
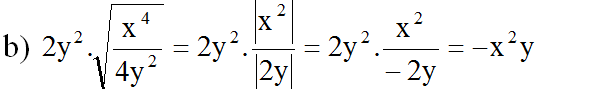
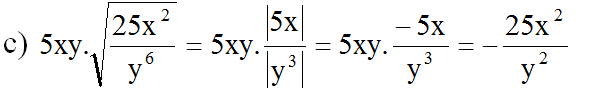
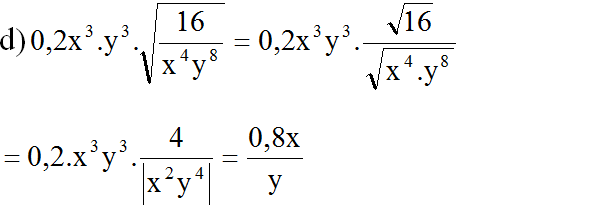
\(\hept{\begin{cases}x^4-x^3+3x^2-4y-1=0\left(1\right)\\\sqrt{\frac{x^2+4y^2}{2}}+\sqrt{\frac{x^2+2xy+4y^2}{3}=x+2y}\end{cases}}\)
Ta có: \(\frac{x^2+4y^2}{2}=\frac{2\left(x^2+4y^2\right)}{4}=\frac{\left(1^2+1^2\right)\left(x^2+4y^2\right)}{4}\ge\frac{\left(x+2y^2\right)}{4}\)( bunhiacopxki )
\(\Rightarrow\sqrt{\frac{x^2+4y^2}{2}}\ge\frac{x+2y}{2}\)
Lại có: \(\sqrt{\frac{x^2+2xy+4y^2}{3}}\ge\frac{x+2y}{2}\)( 2)
Chứng minh: Đẳng thức cần chứng minh \(\Leftrightarrow\frac{x^2+2xy+4y^2}{3}\ge\frac{x^2+4xy+4y^2}{4}\)
\(\Leftrightarrow4x^2+8xy+16y^2\ge3x^2+12xy+12y^2\)
\(\Leftrightarrow x^2-4xy+4y^2\ge0\)
\(\Leftrightarrow\left(x-2y\right)^2\ge0;\forall x,y\)
=> (2) đúng )
\(\Rightarrow\sqrt{\frac{x^2+4y^2}{2}}+\sqrt{\frac{x^2+2xy+4y^2}{3}}\ge x+2y\)
Dấu "=" xảy ra \(\Leftrightarrow x=2y\)
Thay x=2y vào (1) ta được:
\(x^4-x^3+3x^2-2x-1=0\)
\(\Leftrightarrow x^3\left(x-1\right)+3x\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\left(tm\right)\Rightarrow y=\frac{1}{2}\\x^2+3x+1=0\left(3\right)\end{cases}}\)
\(\Delta_{\left(3\right)}=3^2-4=5>0\)
\(\Rightarrow\)pt (3) có 2 nghiệm phân biệt \(\orbr{\begin{cases}x=\frac{-3+\sqrt{5}}{2}\Rightarrow y=\frac{-3+\sqrt{5}}{4}\\x=\frac{-3-\sqrt{5}}{2}\Rightarrow y=\frac{-3-\sqrt{5}}{4}\end{cases}}\)
Vậy ...