tìm số tự nhiên y, biết 1/6+1/12+1/20+...+1/90=6/y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(36\cdot25+35\cdot50-6\cdot25\)
\(=25\cdot\left(36-6\right)+35\cdot50\)
\(=25\cdot30+35\cdot2\cdot25\)
\(=25\cdot\left(30+70\right)=25\cdot100=2500\)
36 x 25 + 35 x 50 - 6 x 25
= 36 x 25 + 35 x 50 - 6 x 25
= 36 x 25 + 35 x 2 x 25 - 6 x 25
= 25 x (36 + 35 x 2 - 6)
= 25 x (36 + 70 - 6)
= 25 x (36 - 6 + 70)
= 25 x (30 + 70)
= 25 x 100
= 2500

Ta có: \(\left(x-3\right)\left(x-1\right)-x\left(2-x\right)=0\)
=>\(x^2-4x+3-2x+x^2=0\)
=>\(2x^2-6x+3=0\)
=>\(x^2-3x+\dfrac{3}{2}=0\)
=>\(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{9}{4}+\dfrac{3}{2}=0\)
=>\(\left(x-\dfrac{3}{2}\right)^2-\dfrac{3}{4}=0\)
=>\(\left(x-\dfrac{3}{2}\right)^2=\dfrac{3}{4}\)
=>\(\left[{}\begin{matrix}x-\dfrac{3}{2}=\dfrac{\sqrt{3}}{2}\\x-\dfrac{3}{2}=-\dfrac{\sqrt{3}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{3}}{2}\\x=\dfrac{3-\sqrt{3}}{2}\end{matrix}\right.\)

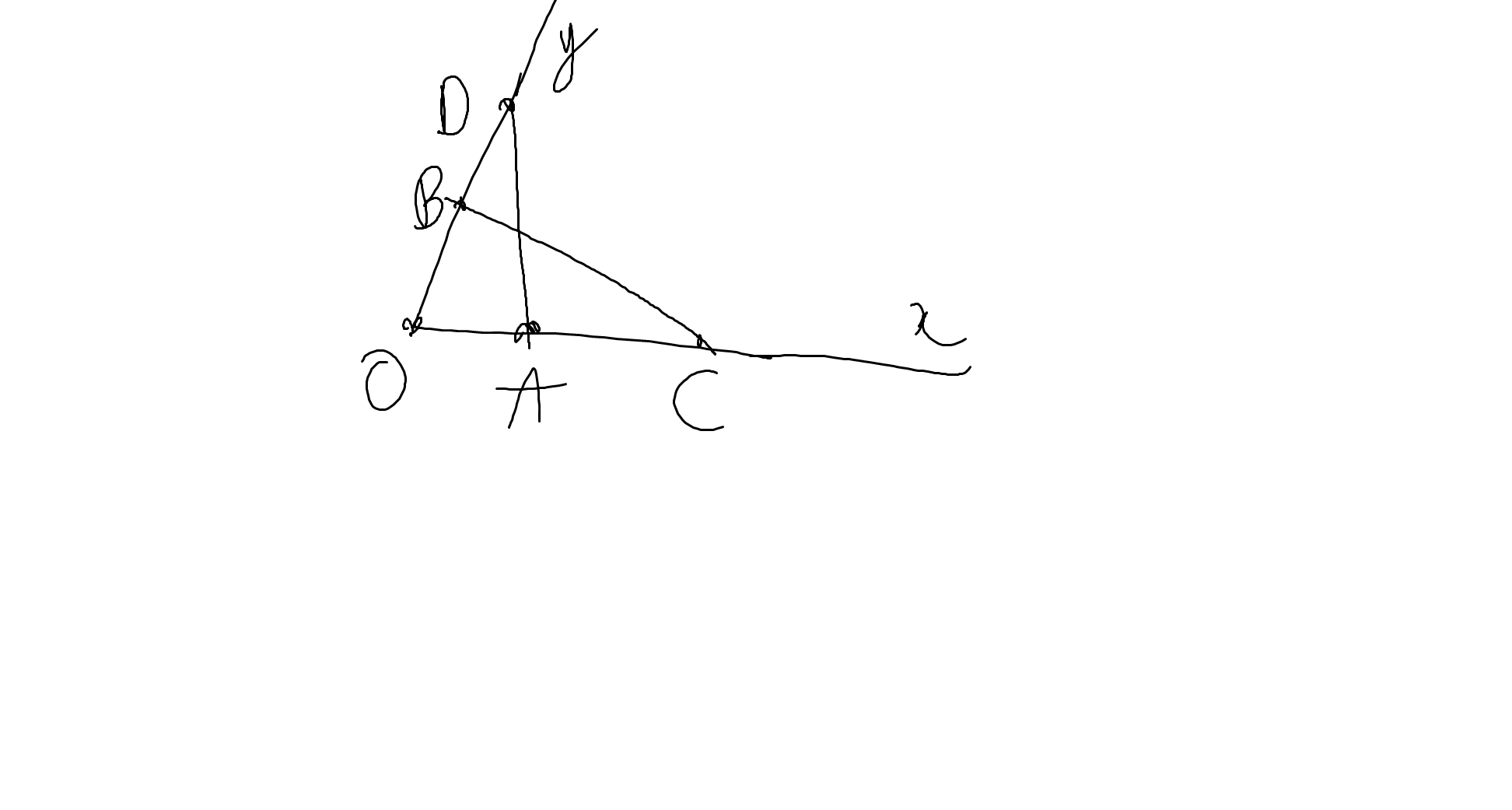
a: Ta có: mn//xy
=>\(\widehat{mAB}=\widehat{ABy}\)(hai góc so le trong)
=>\(\widehat{mAB}=60^0\)
b:
Ta có: \(\widehat{yBc}+\widehat{yBA}=180^0\)(hai góc kề bù)
=>\(\widehat{yBc}=180^0-60^0=120^0\)
Bz là phân giác của góc yBc
=>\(\widehat{yBz}=\widehat{cBz}=\dfrac{\widehat{yBc}}{2}=\dfrac{120^0}{2}=60^0\)
Ta có: \(\widehat{nAB}+\widehat{mAB}=180^0\)(hai góc kề bù)
=>\(\widehat{nAB}=180^0-60^0=120^0\)
At là phân giác của góc nAB
=>\(\widehat{nAt}=\widehat{tAB}=\dfrac{\widehat{nAB}}{2}=\dfrac{120^0}{2}=60^0\)
Ta có: \(\widehat{ABz}=\widehat{ABy}+\widehat{yBz}=60^0+60^0=120^0\)
Ta có: \(\widehat{ABz}+\widehat{BAt}=120^0+60^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên At//Bz

Bài 1:
B = \(x^2\) - 2\(xy\) + 2y2
Thay \(x=13\) và y = 3 vào B ta được
B = 132 - 2.13.3 + 2.32
B = 169 - 26.3 + 2.9
B = 169 - 78 + 18
B = 91 + 18
B = 109

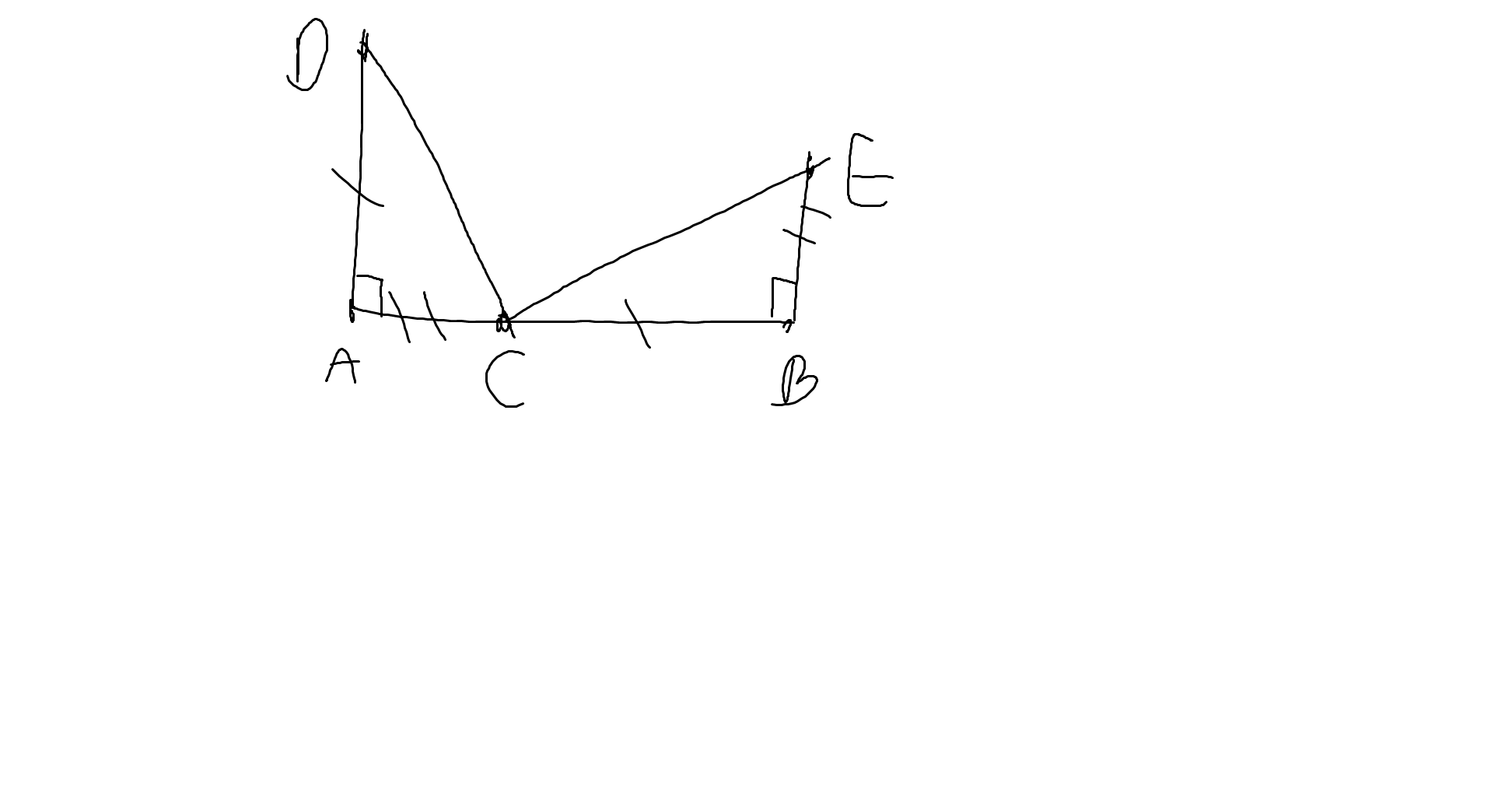
a: Xét ΔDAC vuông tại A và ΔCBE vuông tại B có
DA=CB
AC=BE
Do đó: ΔDAC=ΔCBE
b: ΔDAC=ΔCBE
=>\(\widehat{DCA}=\widehat{CEB}\)
=>\(\widehat{DCA}+\widehat{ECB}=90^0\)
Ta có: \(\widehat{DCA}+\widehat{ECB}+\widehat{DCE}=180^0\)
=>\(\widehat{DCE}+90^0=180^0\)
=>\(\widehat{DCE}=90^0\)
=>CD\(\perp\)CE

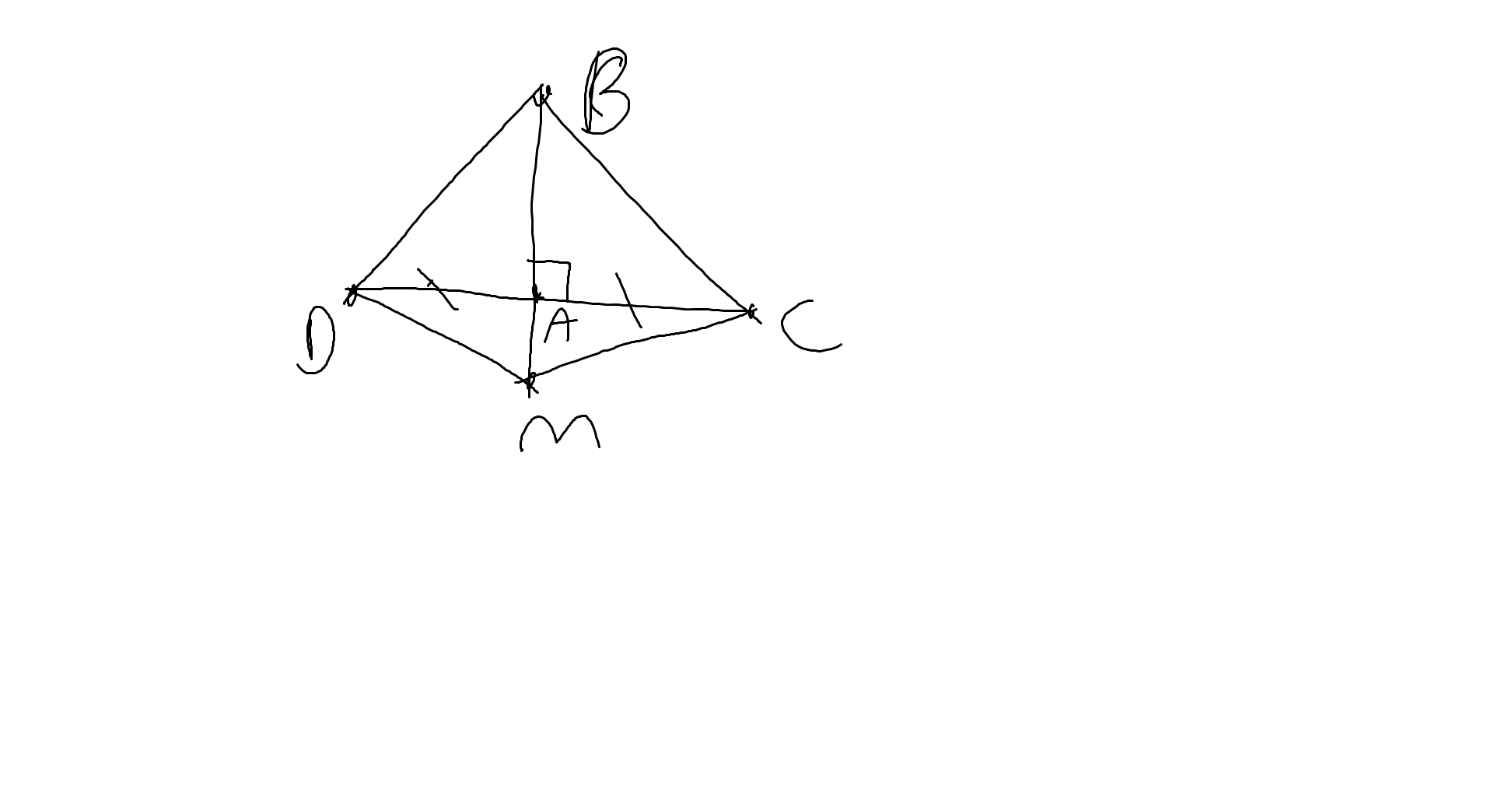
Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
=>AD=BC

Giải:
Chiều rộng của thửa ruộng là: 40 x \(\dfrac{1}{4}\) = 10 (m)
Diện tích thửa ruộng là: 40 x 10 = 400 (m2)
400m2 gấp 100m2 số lần là: 400 : 100 = 4 (lần)
Trên cả thửa ruộng thu được số thóc là: 80 x 4 = 320 (kg)
320 kg = 0,32 tấn
Đáp số: 0,32 tấn thóc
Chiều rộng thửa ruộng là:
\(40\times\dfrac{1}{4}=10\left(m\right)\)
Diện tích thửa ruộng là:
40x10=400(m2)
Khối lượng thóc thu hoạch được là:
\(400:100\times80=320\left(kg\right)=0,32\left(tấn\right)\)

Đây là dạng toán nâng cao, chuyên đề lập số theo điều kiện cho trước. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp khử như sau:
Giải:
Số thứ hai lúc sau hơn số thứ hai lúc đầu là:
3 - 1 = 2 (lần số thứ hai lúc đầu)
Hai lần số thứ hai lúc đầu là: 87 - 69 = 18
Số thứ hai lúc đầu là: 18 : 2 = 9
Số thứ nhất lúc đầu là: 69 - 9 = 60
Đáp số: Số thứ nhất ban đầu là 60; số thứ hai ban đầu là 9.

a: Xét ΔABD vuông tại A và ΔABC vuông tại A có
AB chung
AD=AC
Do đó: ΔABD=ΔABC
b: ΔABD=ΔABC
=>BD=BC
ΔABD=ΔABC
=>\(\widehat{ABD}=\widehat{ABC}\)
=>\(\widehat{MBC}=\widehat{MBD}\)
Xét ΔMBC và ΔMBD có
MB chung
\(\widehat{MBC}=\widehat{MBD}\)
BC=BD
Do đó: ΔMBC=ΔMBD
\(\dfrac{1}{6}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + .. + \(\dfrac{1}{90}\) = \(\dfrac{6}{y}\)
\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\)+ ... + \(\dfrac{1}{9.10}\) = \(\dfrac{6}{y}\)
\(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}-\dfrac{1}{5}\) + .. + \(\dfrac{1}{9}-\dfrac{1}{10}\) = \(\dfrac{6}{y}\)
\(\dfrac{1}{2}\) - \(\dfrac{1}{10}\) = \(\dfrac{6}{y}\)
\(\dfrac{2}{5}\) = \(\dfrac{6}{y}\)
y = 6 : \(\dfrac{2}{5}\)
y = 15
\(\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{90}=\dfrac{6}{y}\)
=>\(\dfrac{6}{y}=\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+...+\dfrac{1}{9\times10}\)
=>\(\dfrac{6}{y}=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
=>\(\dfrac{6}{y}=\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{5}{10}-\dfrac{1}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)
=>\(y=5\times\dfrac{6}{2}=15\)