:^ 

quệ mọe

Trả lời nhanh giúp mình với

Khi đổ dầu từ thùng 1 sang thùng 2 thì số lượng dầu của 2 thùng không đổi .

Thùng 1 lúc đầu :

 37,5 : ( 2 + 3 ) x 2 + 2,5 = 17,5 ( lít )  

Thùng 2 lúc đầu :

37,5 - 17,5 = 20 ( lít )

    Đ/S :......

:33

Hình như bài toán này thiếu thông tin (x+7y) chia hết cho 31 thì phải nên cho mình xin cả cái đề bài cụ thể thì mình mới giải được nhá :))

19x20x21x88x89x90

tick nha

a.

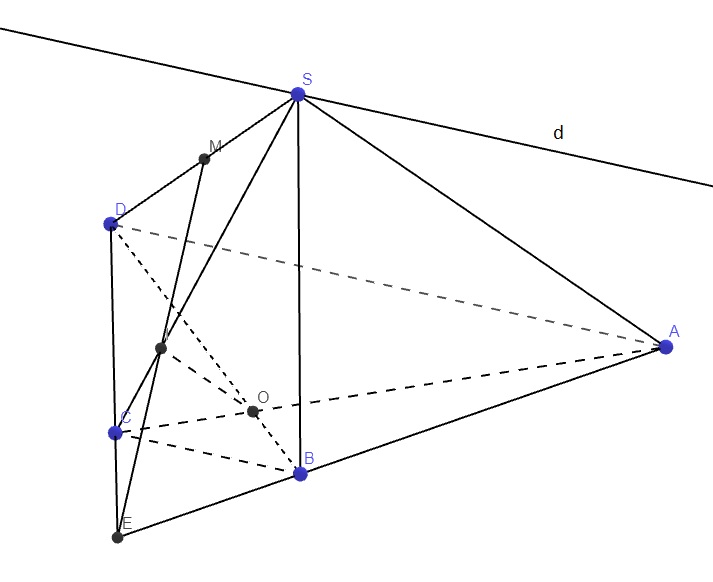
Do S là 1 điểm chung của (SAD) và (SBC) đồng thời \(AD||BC\Rightarrow\) giao tuyến của (SAD) và (SBC) là đường thẳng đi qua S và song song AD

Qua S kẻ đường thẳng d song song AD

\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)

b.

Kéo dài AB và CD cắt nhau tại E

Trong mp (SCD), nối EM cắt SC tại I

\(\Rightarrow I=SC\cap\left(MAB\right)\)

c.

Do AD song song BC, áp dụng định lý Talet:

\(\dfrac{OC}{OA}=\dfrac{BC}{AD}=\dfrac{1}{3}\Rightarrow OC=\dfrac{1}{3}OA=\dfrac{1}{3}\left(AC-OC\right)\)

\(\Rightarrow OC=\dfrac{1}{4}AC\Rightarrow\dfrac{OC}{AC}=\dfrac{1}{4}\) (1)

Cũng theo talet: \(\dfrac{EC}{ED}=\dfrac{BC}{AD}=\dfrac{1}{3}\)

Áp dụng định lý Menelaus cho tam giác SCD:

\(\dfrac{IS}{IC}.\dfrac{CE}{DE}.\dfrac{DM}{MS}=1\Leftrightarrow\dfrac{IS}{IC}.\dfrac{1}{3}.1=1\)

\(\Rightarrow IC=\dfrac{1}{3}IS=\dfrac{1}{3}\left(SC-IC\right)\Rightarrow IC=\dfrac{1}{4}SC\)

\(\Rightarrow\dfrac{IC}{SC}=\dfrac{1}{4}\) (2)

(1);(2) \(\Rightarrow\dfrac{IC}{SC}=\dfrac{OC}{AC}\Rightarrow OI||SA\Rightarrow SA||\left(BID\right)\)

Gọi chiều dài của các tấm vải 1,2,3 lần lượt là a,b,c

Sau khi cắt tấm 1 còn: a - 1/9a = 8/9a

Sau khi cắt tấm 2 còn b - 3/7b = 4/7b

Sau khi cắt tấm 3 còn c - 1/3c = 2/3c

Theo đề bài ta có 8/9a = 4/7b = 2/3c

Áp dụng tính chất dãy tỉ số bằng nhau 

⇒ 8/9a = 4/7b = 2/3c = a/(8/9) = b/(7/4) = c/(3/2) = (a+b+c)/(8/9+7/4+3/2) = 24

Vậy tấm 1 dài a = 24*9/8 = 27 (m)

        tấm 2 dài b = 24*7/4 = 42 (m)

         tấm 3 dài c = 24*3/2 = 36 (m)

( vẫn còn 1 cách giải nữa là vẽ hình 3 đoạn thẳng tượng trưng cho 3 tấm vải rồi giải như bình thường)

1.c

2.d

3.d

4.b

5.a

câu 5 mình chưa chắc đâu nha

    giúp mình với ạ! Cảm on nhìu nhìu

4^x+2-15=49

4^x+2      =49+15

4^x+2      =64

4^x+2      =4³

4^x         =4^3-2

4^x         =4¹

⇒x        =1

\(4^{x+2}=49+15\\ 4^{x+2}=64\\ 4^{x+2}=4^3\\ 4^x=4^{3-2}\\ 4^x=4^1\\ \Rightarrow x=1\)