pt <=> \(\left(3x+1+x-7\right)\left(\left(3x+1\right)^2+\left(x-7\right)^2\right)=\left(4x-6\right)^3\)

\(\Leftrightarrow\left(4x-6\right)\left(9x^2+6x+1+x^2-14x+49-\left(4x-6\right)^2\right)=0\)

\(\Leftrightarrow\left(2x-3\right)\left(10x^2-8x+50-16x^2+48x-36\right)=0\)

\(\orbr{\begin{cases}2x-3=0\\-6x^2+40x+14=0\end{cases}}\) \(\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{2}\\-3x^2+20x+7=0\left(\cdot\right)\end{cases}}\)

pt(*) <=> (3x-1)(x+7)=0 <=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=-7\end{cases}}\)

Vậy x=...

=a  ( a^3+1)  (a^3-1 )

= a( a+1)(a^2-a+1)(a-1)(a^2+a+1)

=a(a-1)(a+1)(a^2-a+1)(a^2+a+1)

=a(a-1)(a+1)(a^2-a+1-7)(a^2+a+1)

+7a(a-1)(a+1)(a^2+a-1)

=a(a-1)(a+1)(a^2-a-6)(a^2+a+1-7)

+7a(a-1)(a+1)(a^2+a-1)

+7a(a-1)(a+1)(a^2-a-6)

Ta có: 7a(a-1)(a+1)(a^2+a-1)+7a(a-1)(a+1)(a^2-a-6) chia hết cho 7( cùng có nhân tử 7)

Ta cần chứng minh: a(a-1)(a+1)(a^2-a-6)(a^2+a+1-7) chia hết cho 7

Ta có: a(a-1)(a+1)(a^2-a-6)(a^2+a+1-7)

=a(a-1)(a+1) [(a+2)(a-3) [(a-2)(a+3)]

=(a-3)(a-2)(a-1) a(a+1)(a+2)(a+3) là tích của 7 số nguyên liên tiếp nên chia hết cho 7

Em chịu vì em học lớp 6 mà nhưng anh hay chị gì đó có thể kết bạn với em không?

Ta có hình như sau :

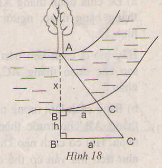
giải :

Ta có:

 =  mà AB' = x + h nên 

 =  <=> a'x = ax + ah

<=> a'x - ax = ah

<=> x(a' - a) = ah

x= 

Vậy khoảng cách AB bằng 

Ta có hình như sau :

Giải

Ta có:

 =  mà AB' = x + h nên 

 =  <=> a'x = ax + ah

<=> a'x - ax = ah

<=> x(a' - a) = ah

x= 

Vậy khoảng cách AB bằng 

Ta có:

\(\frac{a^2}{b^2}+1\ge2.\frac{a}{b}\)

\(\frac{b^2}{c^2}+1\ge2.\frac{b}{c}\)

\(\frac{c^2}{a^2}+1\ge2.\frac{c}{a}\)

Cộng vế theo vế ta được

\(\frac{a^2}{b^2}+\frac{b^2}{c^2}+\frac{c^2}{a^2}+3\ge2\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)\)

\(\Leftrightarrow\frac{a^2}{b^2}+\frac{b^2}{c^2}+\frac{c^2}{a^2}\ge\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)-3\)

\(\ge\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+3\sqrt{\frac{a}{b}.\frac{b}{c}.\frac{c}{a}}-3=\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\)
Dấu =  xảy ra khi a = b = c

Ta co: \(\frac{a^2}{b^2}\ge\frac{a}{b}\); \(\frac{b^2}{c^2}\ge\frac{b}{c}\);\(\frac{c^2}{a^2}\ge\frac{c}{a}\)\(\Rightarrow dpcm\)

\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+2008=\left(x+2\right)\left(x+8\right)\left(x+4\right)\left(x+6\right)+2008\)

\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)\)

đặt \(x^2+10x+21=a\)

ta có \(\left(a-5\right)\left(a+3\right)=a^2-2a-15+2008=a\left(a-2\right)+1993\)

ta có a(a-2) chia hết cho a hay x^2+10x+21

số dư là 1993