Tam giác ABC vuông tại A có đường cao AH. biết AB = 4cm, HC = 15cm. Tính độ dài đoạn thẳng BH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(AB^2=BH.BC=\frac{1}{5}BC.BC\)
\(\Rightarrow BC=\sqrt{5AB^2}=10\left(cm\right)\)

Ko đăng linh tinh lên diễn đàn
Đây ko phải là toán


Đề có đoạn sai mình sửa nhé
Ta có: \(a+b+c=\frac{1}{abc}\Rightarrow abc\left(a+b+c\right)=1\)
Lại có: \(1+b^2c^2=abc\left(a+b+c\right)+b^2c^2=bc\left(a^2+ab+ca+bc\right)=bc\left(a+b\right)\left(a+c\right)\)
Tương tự: \(\hept{\begin{cases}1+c^2a^2=ca\left(b+c\right)\left(a+b\right)\\1+a^2b^2=ab\left(c+a\right)\left(b+c\right)\end{cases}}\)
Khi đó: \(P=\sqrt{\frac{\left(1+b^2c^2\right)\left(1+c^2a^2\right)}{c^2\left(1+a^2b^2\right)}}=\sqrt{\frac{bc\left(a+b\right)\left(a+c\right)\cdot ca\left(b+c\right)\left(b+a\right)}{abc^2\left(c+a\right)\left(c+b\right)}}\)
\(=\sqrt{\left(a+b\right)^2}=\left|a+b\right|=a+b\) vì \(a,b\ge0\)

\(\sqrt{x^2-2x+4}+1\)
\(=\sqrt{x^2-2x+1+3}+1\)
\(=\sqrt{\left(x-1\right)^2+3}+1\)
Có
\(\left(x-1\right)^2+3\ge3\forall x\)
\(\sqrt{\left(x-1\right)^2+3}\ge\sqrt{3}\)
\(\sqrt{\left(x-1\right)^2+3}+1\ge\sqrt{3}+1\)
Dấu = xảy ra khi và chỉ khi
x - 1 = 0
x = 1
Vậy min = \(\sqrt{3}+1\) khi và chỉ khi x = 1

a, A xác định khi : \(-1\le x\le1\)
\(=\frac{\sqrt{\frac{\left(\sqrt{1-x}-\sqrt{1+x}\right)^2}{2}}.\left[\left(\sqrt{1+x}+\sqrt{1-x}\right)\left(2-\sqrt{1-x^2}\right)\right]}{2-\sqrt{1-x^2}}\)
\(=\frac{\left|\sqrt{1-x}-\sqrt{1+x}\right|.\left(\sqrt{1+x}+\sqrt{1-x}\right)}{\sqrt{2}}=\hept{\begin{cases}\sqrt{2x}khi0\le x\le1\\-\sqrt{2x}khi-1\le x\le0\end{cases}}\)
b, \(A\ge\frac{1}{2}\)
Khi \(0\le x\le1\)thì \(\sqrt{2x}\ge\frac{1}{2}\Leftrightarrow x\ge\frac{1}{2\sqrt{2}}\)
Khi \(-1\le x\le0\)thì \(-\sqrt{2x}\ge\frac{1}{2}\Leftrightarrow x\le-\frac{1}{2\sqrt{2}}\)
Vậy \(A\ge\frac{1}{2}\)\(\Leftrightarrow-1\le x\le-\frac{1}{2\sqrt{2}}\)hoặc \(\frac{1}{2\sqrt{2}}\le x\le1\)
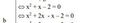

\(AB^2=BH.BC=HB.\left(HB+HC\right)=HB^2+15HB\)
\(\Leftrightarrow HB^2+15HB=16\Leftrightarrow HB=1\left(cm\right)\)