Cho hình thang ABCD có AB//CD. Biết AB=26cm; CD=10cm và đường chéo AC vuông góc với cạnh bên BC. Tính diện tích hình thang ABCD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: C = \(\frac{x+10}{\sqrt{x}+3}=\frac{x-9+19}{\sqrt{x}+3}=\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+19}{\sqrt{x}+3}=\sqrt{x}-3+\frac{19}{\sqrt{x}+3}\)
C = \(\sqrt{x}+3+\frac{19}{\sqrt{x}+3}-6\ge2.\sqrt{\left(\sqrt{x}+3\right)\cdot\frac{19}{\left(\sqrt{x}+3\right)}}-6\)(bđt cosi)
C \(\ge2\sqrt{19}-6\)
Dấu "=" xảy ra <=> \(\sqrt{x}+3=\frac{19}{\sqrt{x}+3}\) <=> \(\left(\sqrt{x}+3\right)^2=19\)
<=> \(\orbr{\begin{cases}\sqrt{x}+3=\sqrt{19}\\\sqrt{x}+3=-\sqrt{19}\left(vn\right)\end{cases}}\) <=> \(\sqrt{x}=\sqrt{19}-3\) <=> \(x=22-6\sqrt{19}\)
Vậy MinC = \(2\sqrt{19}-6\) <=> \(x=22-6\sqrt{19}\)

\(\hept{\begin{cases}\left(5x-4y\right)\left(3x+2y\right)=7y-2x\\\left(5y-4x\right)\left(3y+2x\right)=7x-2y\end{cases}}\)
<=>\(\hept{\begin{cases}15x^2-2xy-8y^2=7y-2x\left(1\right)\\15y^2-2xy-8x^2=7x-2y\end{cases}}\)
<=> \(15x^2-2xy-8y^2-15y^2+2xy+8x^2=7y-2x-7x+2y\)
<=> \(23x^2-23y^2-9y+9x=0\)
<=> \(23\left(x-y\right)\left(x+y\right)-9\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(23x+23y-9\right)=0\)
<=> \(\orbr{\begin{cases}x=y\\x+y=\frac{9}{23}\end{cases}}\)
Với x = y => thay vào pt (1)
<=> \(15x^2-2x^2-8x^2=7x-2x\)
<=> \(5x^2-5x=0\) <=> \(5x\left(x-1\right)=0\)
<=> \(\orbr{\begin{cases}x=0\\x=1\end{cases}}\) => \(\orbr{\begin{cases}x=y=0\\x=y=1\end{cases}}\)
Với \(x+y=\frac{9}{23}\) => \(y=\frac{9}{23}-x\)thay vào pt (1)
Ta có: \(15x^2-2x\left(\frac{9}{23}-x\right)-8\left(\frac{9}{23}-x\right)^2=7\left(\frac{9}{23}-x\right)-2x\)
<=> \(15x^2-\frac{18}{23}x+2x^2-8\left(\frac{81}{529}-\frac{18}{23}x+x^2\right)=\frac{63}{23}-7x-2x\)
<=> \(17x^2-\frac{18}{23}x-\frac{648}{529}+\frac{144}{23}x-8x^2-\frac{63}{23}+9x=0\)
<=> \(9x^2+\frac{333}{23}x-\frac{2097}{529}=0\) (phần còn lại tự làm)


\(a,\sqrt{29+12\sqrt{5}}+2\sqrt{21-8\sqrt{5}}\)
\(\sqrt{29+6\sqrt{20}}+\sqrt{84-32\sqrt{5}}\)
\(\sqrt{\sqrt{20}^2+6\sqrt{20}+3^2}+\sqrt{84-16\sqrt{20}}\)
\(\sqrt{\left(\sqrt{20}+3\right)^2}+\sqrt{8^2-16\sqrt{20}+\sqrt{20}^2}\)
\(\left|\sqrt{20}+3\right|+\sqrt{\left(8-\sqrt{20}\right)^2}\)
\(\sqrt{20}+3+\left|8-\sqrt{20}\right|\)
\(\sqrt{20}+3+8-\sqrt{20}\)
\(=11\)

Ta có: \(\sqrt{9-4\sqrt{5}}-\sqrt{5}=\sqrt{5-4\sqrt{5}+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2\)
Vayyj ...
Ta có : VT= \(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
=\(\sqrt{5-4\sqrt{5}+4}\)\(-\sqrt{5}\)
=\(\sqrt{\left(\sqrt{5}\right)^2-2.2\sqrt{5}+2^2}\)\(-\sqrt{5}\)
=\(\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
=\(\left|\sqrt{5}-2\right|-\sqrt{5}\)
=\(\sqrt{5}-2-\sqrt{5}\)
=\(-2\)=VP

Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),

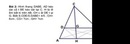
Hạ CH vuông với AB tại H
Ta có : \(HB=\frac{AB-CD}{2}=8\left(cm\right)\)
\(\Rightarrow BC^2=HB.AB=8.26\)
\(\Rightarrow BC=4\sqrt{3}\)
\(\Rightarrow HC=\sqrt{BC^2-HB^2}=12\)
\(\Rightarrow S_{ABCD}=\frac{HC.\left(AB+CD\right)}{2}=\frac{12.\left(26+10\right)}{2}=216\left(cm^2\right)\)
Ps : nhớ k ạ :33
# Aeri #
BC=4\(\sqrt{ }\)13 chứ