Ta có: `\hat{xOy}+\hat{xOz}=180^o` (`2` góc kề bù)

  `=>120^o +\hat{xOz}=180^o`

  `=>\hat{xOz}=60^o`

Vì `Om` là tia p/g của `\hat{xOy}=>\hat{xOm}=1/2\hat{xOy}=1/2 .120^o=60^o`

Ta có: `\hat{xOm}+\hat{xOz}=\hat{mOz}`

   `=>\hat{mOz}=60^o +60^o =120^o`

Vì Om là phân giác của \(\widehat{mOz}\)

\(\Rightarrow\widehat{xOm}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}.120^o=60^o\)

Vì \(\widehat{xOy}\) và \(\widehat{xOz}\) là 2 góc kề bù 

\(\Rightarrow\widehat{xOz}=180^o-120^o=60^o\) 

\(\Rightarrow\widehat{mOz}=\widehat{xOz}+\widehat{xOm}=60^0.2=120^o\)

\(x-2=\left(x-2\right)^2\)

\(x-2-\left(x-2\right)^2=0\)

\(\left(x-2\right)\left(1-x+2\right)=0\)

\(\left(x-2\right)\left(3-x\right)=0\) (*nếu chỉ cần phân tích thì đến đây thôi !!!*)

=> x-2=0     hoặc       3-x=0

     x=2                         x=3

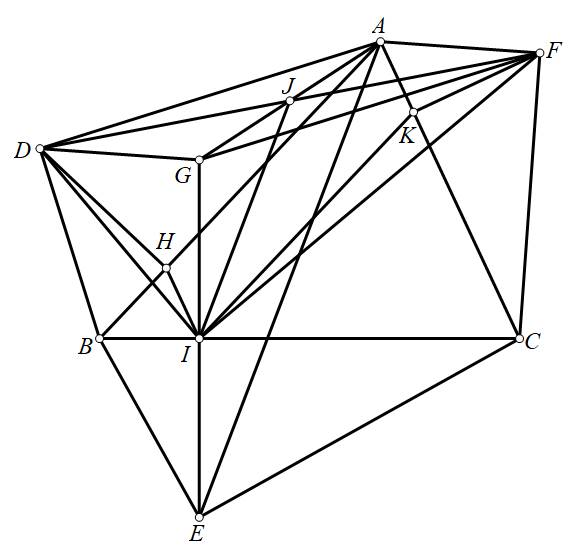
Lấy \(H,I,K\) trên \(AB,BC,CA\) sao cho \(DH,EI,FK\) tương ứng vuông góc với \(AB,BC,CA\). Lấy \(G\) đối xứng với \(E\) qua \(BC\). Gọi \(AG\) cắt \(DF\) tại \(J\).

Ta thấy \(\Delta BGC=\Delta BEC\sim\Delta BDA\sim\Delta AFC\). Suy ra \(\Delta BDG~\Delta BAC\sim GFC\). Từ đây \(\dfrac{DG}{AC}=\dfrac{BD}{BA}=\dfrac{AF}{AC}\Rightarrow DG=AF\). Tương tự thì \(FG=AD\). Do đó \(ADGF\) là hình bình hành. Suy ra \(J\) là trung điểm của \(DF,AG.\) 

Ta có \(IK||AB\) do \(\dfrac{IB}{IC}=\dfrac{EB^2}{EC^2}=\dfrac{AF^2}{AC^2}=\dfrac{KA}{KC}\) và \(IH||AC\)

Suy ra \(\Delta DHI\sim\Delta IKF\) vì \(\widehat{DHI}=\widehat{IKF}=90^0+\widehat{BAC}\) và \(\dfrac{DH}{IK}=\dfrac{DH}{AH}=\dfrac{AK}{KF}=\dfrac{HI}{KF}\) . Do vậy:\(\widehat{DIF}=\widehat{DIH}+\widehat{HIK}+\widehat{KIF}=\widehat{DIH}+\widehat{BAC}+\widehat{DHI}=180^0-\left(90^0+\widehat{BAC}\right)+\widehat{BAC}=90^0\)Xét \(\Delta AGE\) có đường trung bình \(IJ\). Suy ra \(AE=2IJ\)

Xét \(\Delta DIF\) có \(\widehat{DIF}=90^0\), \(J\) là trung điểm của \(DF\). Suy ra \(DF=2IJ\)

Vậy \(DF=AE.\)

\(\dfrac{3^{12}+3^{15}}{1+3^3}\)

\(=\dfrac{3^{12}\left(1+3^3\right)}{1+3^3}\)

\(=3^{12}\)

\(\dfrac{3^{12}+3^{15}}{1+3^3}=\dfrac{3^{12}\left(1+3^3\right)}{1+3^3}=3^{12}\)

`9/21 + 6/49 =3/7 + 6/49 + 21/49 = (21+6)/49 = 27/49`

\(\dfrac{9}{21}+\dfrac{6}{49}\)

\(=\dfrac{3}{7}+\dfrac{6}{49}\)

\(=\dfrac{21}{49}+\dfrac{6}{49}\)

\(=\dfrac{21+6}{49}=\dfrac{27}{49}\)

\(\dfrac{-2}{3}=\dfrac{7}{x}\)

\(=>-2x=3.7=21\)

\(=>x=\dfrac{-21}{2}\)

a) Đáy nhỏ là :

70 x 35% = 24,5 ( m )

Chiều cao là :

70 x 60%= 42 ( m )

Diện tích thửa ruộng là :

( 70 + 24,5 ) x 42/2 = 1984,5 (m² )

b)1 m² bác Ba thu được :

53 : 100 = 0,53 (kg )

1984,5 m² bác Ba thu được :

0,53 x 1984,5 = 1051,785 ( kg )

Độ dài đáy bé :

`70 xx 35% = 24,5(m)`

Chiều cao thửa ruộng :

`70 xx 60% =42(m)`

Diện tích thửa ruộng :

`(70+24,5)xx42:2=1984,5(m^2)`

Số `kg` thóc thu hoạch được :

`1984,5 :100 xx 53= 1051,785(kg)`

Đ/s...

Diện tích tam giác ABC là :

20 : 1/2 = 40 ( dm² )

Đáp số : 40 dm²

Bài giải

Diện tích tam giác ABC là :

20 : 1/2 = 40 ( dm2 )

Đáp số : 40 dm2

Tick cho mình nhé