mn giải giúp e với ạ
mn giải giúp e với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi M là trung điểm EG \(\Rightarrow AM\perp EG\) (tam giác cân)
\(\Rightarrow AM\perp\left(EFGH\right)\Rightarrow AM=d\left(A;\left(EFGH\right)\right)\)
\(EG=30-2x\Rightarrow EM=\dfrac{1}{2}EG=15-x\)
\(\Rightarrow AM=\sqrt{AE^2-EM^2}=\sqrt{x^2-\left(15-x\right)^2}=\sqrt{30x-225}\)
Do AEG là tam giác, theo BĐT tam giác: \(\left\{{}\begin{matrix}AE+AG>EG\\\left|AG-AE\right|< EG\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+x>30-2x\\0< 30-2x\end{matrix}\right.\) \(\Rightarrow\dfrac{15}{2}< x< 15\)
\(V=AD.S_{\Delta AEG}=30.\dfrac{1}{2}AM.EG=15.\left(30-2x\right)\sqrt{30x-225}\)
\(V^2=15^3.4\left(15-x\right)^2\left(2x-15\right)=15^3.4.\left(15-x\right)\left(15-x\right)\left(2x-15\right)\)
\(\le15^3.4.\left(\dfrac{15-x+15-x+2x-15}{3}\right)^3=...\)
Dấu "=" xảy ra khi \(15-x=2x-15\Rightarrow x=10\)
\(\Rightarrow d\left(A;\left(EFGH\right)\right)=AM=\sqrt{30.10-225}=5\sqrt{3}\)

S A B C D H K
a/
Ta có
ABCD là HCN (gt) \(\Rightarrow BC\perp AB\)
\(SA\perp\left(ABCD\right);BC\in\left(ABCD\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp AB;BC\perp SA\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\in\left(SBC\right)\)
\(\Rightarrow BC\perp SB\) => tg SBC vuông tại B
b/ Chứng minh tương tự cũng có
\(CD\perp\left(SAD\right)\) mà \(SD\in\left(SCD\right)\)
\(\Rightarrow CD\perp SD\) => tg SCD vuông tại D
c/
Ta có
\(BC\perp\left(SAB\right)\left(cmt\right);AH\in\left(SAB\right)\Rightarrow AH\perp BC\)
mà \(AH\perp SB\left(gt\right)\)
\(\Rightarrow AH\perp\left(SBC\right)\) mà \(SC\in\left(SBC\right)\)
\(\Rightarrow SC\perp AH\)
C/m tương tự ta cũng có \(SC\perp AK\)
\(\Rightarrow SC\perp\left(AHK\right)\)
d/
Ta có
\(SC\perp\left(AHK\right)\left(cmt\right);HK\in\left(AHK\right)\Rightarrow HK\perp SC\)

1.
\(y'=\dfrac{2x+4}{2\sqrt{x^2+4x+3}}=\dfrac{x+2}{\sqrt{x^2+4x+3}}\)
2.
\(f'\left(x\right)=\dfrac{1}{2\sqrt{x+1}}+\dfrac{1}{2\sqrt{x-1}}\)
3.
\(y'=\dfrac{\left(2x+2\right)\left(x-2\right)-\left(x^2+2x+1\right)}{\left(x-2\right)^2}=\dfrac{x^2-4x-5}{\left(x-2\right)^2}\)
4.
\(y'=\dfrac{-6}{\left(6x-5\right)^2}\)
5.
\(y'=\dfrac{2.\left(-1\right)-1.1}{\left(x-1\right)^2}=\dfrac{-3}{\left(x-1\right)^2}\)
6.
\(y'=4x^3+4x\)

Câu 1:
\(y=x^3+2x^2+1\)
=>\(y'=3x^2+2\cdot2x=3x^2+4x\)
\(y'\left(1\right)=3\cdot1^2+4\cdot1=3+4=7\)
Phương trình tiếp tuyến tại x=1 là:
y-f(1)=f'(1)(x-1)
=>y-4=7(x-1)
=>y=7x-7+4=7x-3
Câu 2:
a: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
b: \(S_{ABCD}=AB^2=a^2\)
\(V_{S.ABCD}=\dfrac{1}{3}\cdot SA\cdot S_{ABCD}=\dfrac{1}{3}\cdot3a\cdot a^2=a^3\)

a.
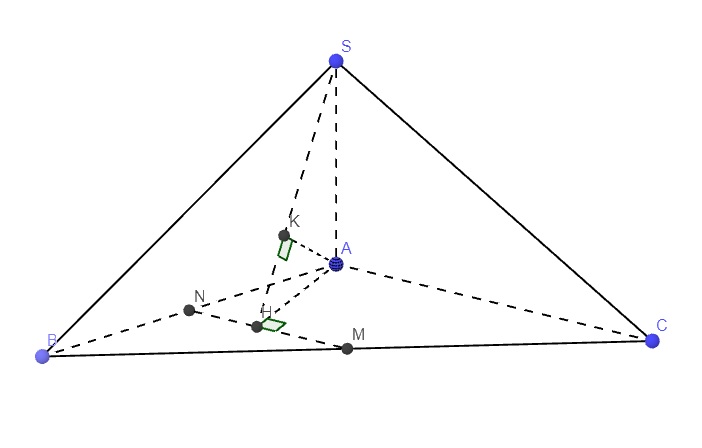
\(S_{\Delta ABC}=\dfrac{1}{2}AB.AC.sinA=\dfrac{1}{2}.a.a.sin120^0=\dfrac{a^2\sqrt{3}}{4}\)
\(\Rightarrow V=\dfrac{1}{3}SA.S_{\Delta ABC}=\dfrac{a^3}{8}\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABC
\(\Rightarrow MN||AC\Rightarrow AC||\left(SMN\right)\)
\(\Rightarrow d\left(SM;AC\right)=d\left(AC;\left(SMN\right)\right)=d\left(A;\left(SMN\right)\right)\)
Từ A kẻ AH vuông góc MN (H thuộc đường thẳng MN)
Từ A kẻ \(AK\perp SH\) (K thuộc SH) (1)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp MN\\AH\perp MN\left(gt\right)\end{matrix}\right.\) \(\Rightarrow MN\perp\left(SAH\right)\)
\(\Rightarrow MN\perp AK\) (2)
(1);(2)\(\Rightarrow AK\perp\left(SMN\right)\Rightarrow AK=d\left(A;\left(SMN\right)\right)\)
AH vuông góc MN, mà AC song song MN \(\Rightarrow AH\perp AC\Rightarrow\widehat{CAH}=90^0\)
\(\Rightarrow\widehat{HAN}=\widehat{BAC}-\widehat{CAH}=120^0-90^0=30^0\)
\(\Rightarrow AH=AN.cos\widehat{HAN}=\dfrac{AB}{2}.cos30^0=\dfrac{a\sqrt{3}}{4}\)
Hệ thức lượng:
\(AK=\dfrac{AH.SA}{\sqrt{AH^2+SA^2}}=\dfrac{a\sqrt{39}}{26}\)

a: ta có: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
SA,AC cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
=>BD\(\perp\)SC

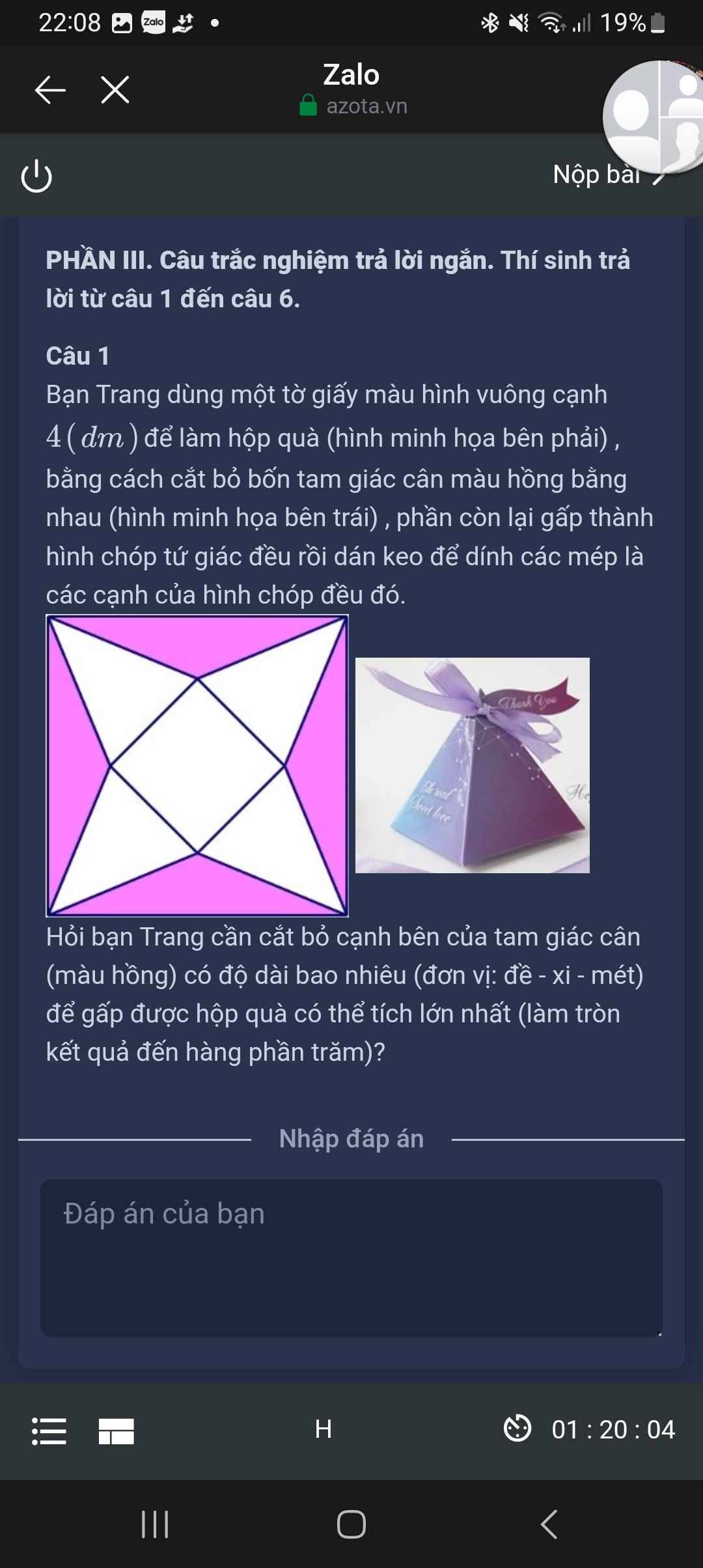
Gọi chiều cao của các tam giác cân màu hồng là x>0
\(\Rightarrow\) Độ dài đường chéo đáy: \(c=4-2x\)
Do đáy là hình vuông nên cạnh hình vuông: \(a=\dfrac{c}{\sqrt{2}}=\dfrac{4-2x}{\sqrt{2}}=2\sqrt{2}-x\sqrt{2}\)
Cạnh của tam giác cân màu hồng: \(l=\sqrt{\left(\dfrac{4}{2}\right)^2+x^2}=\sqrt{x^2+4}\)
Chiều cao chóp: \(h=\sqrt{l^2-\left(\dfrac{c}{2}\right)^2}=\sqrt{x^2+4-\left(2-x\right)^2}=2\sqrt{x}\)
\(V=\dfrac{1}{3}h.a^2=\dfrac{4}{3}.\sqrt{x}.\left(2-x\right)^2\)
\(\Rightarrow V^2=\dfrac{16}{9}x\left(2-x\right)^4=\dfrac{16}{9}.4x.\left(2-x\right)\left(2-x\right)\left(2-x\right)\left(2-x\right)\)
\(\le\dfrac{16}{9}\left(\dfrac{4x+2-x+2-x+2-x+2-x}{5}\right)^5=\dfrac{16}{9}.\left(\dfrac{8}{5}\right)^5\)
Dấu "=" xảy ra khi \(4x=2-x\Rightarrow x=\dfrac{2}{5}\)
\(\Rightarrow\) Cạnh tam giác cân: \(l=\sqrt{x^2+4}=\sqrt{\left(\dfrac{2}{5}\right)^2+4}=\dfrac{2\sqrt{26}}{5}\)

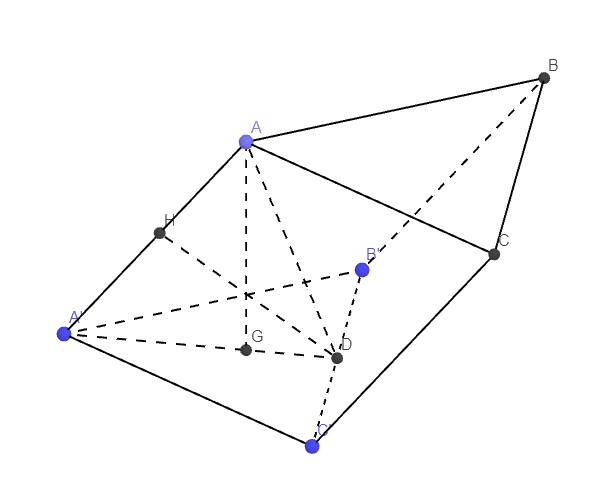
Gọi D là trung điểm B'C' \(\Rightarrow A'D\perp B'C'\) (1)
Mà G là trọng tâm A'B'C' \(\Rightarrow G\in A'D\Rightarrow AG\in\left(A'AD\right)\)
\(AG\perp\left(A'B'C'\right)\Rightarrow AG\perp B'C'\) (2)
(1);(2) \(\Rightarrow BC\perp\left(A'AG\right)\)
Từ D kẻ \(DH\perp A'A\), do \(DH\in\left(A'AD\right)\Rightarrow B'C'\perp DH\)
\(\Rightarrow DH\) là đường vuông góc chung của AA' và B'C'
\(\Rightarrow DH=d\left(AA';B'C'\right)\)
\(A'D=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(A'G=\dfrac{2}{3}A'D=\dfrac{a\sqrt{3}}{3}\) \(\Rightarrow AG=\sqrt{A'A^2-A'G^2}=\dfrac{a\sqrt{6}}{3}\)
\(DH=A'D.sin\widehat{AA'G}=A'D.\dfrac{AG}{A'A}=\dfrac{a\sqrt{2}}{2}\)

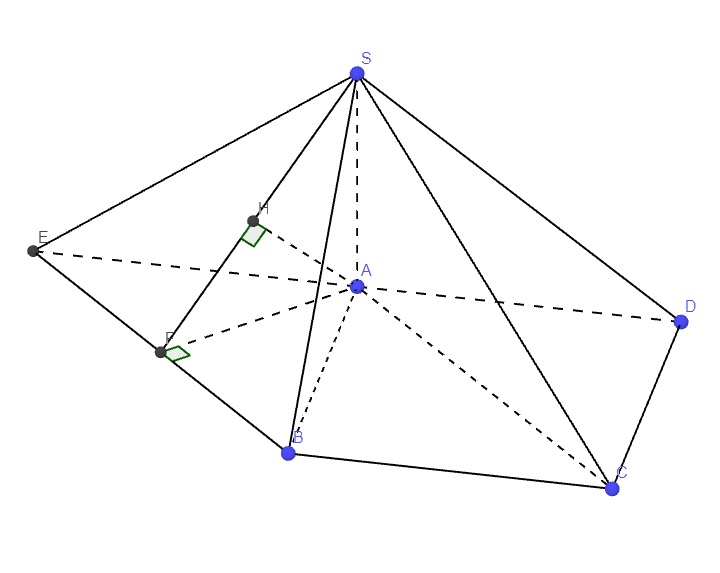
Qua B kẻ đường thẳng song song AC cắt AD kéo dài tại E
Từ A kẻ \(AF\perp BE\) (F thuộc BE), từ A kẻ \(AH\perp SF\) (H thuộc SF)
\(AC||BE\Rightarrow AC||\left(SBE\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
\(\left\{{}\begin{matrix}AF\perp BE\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BE\end{matrix}\right.\) \(\Rightarrow BE\perp\left(SAF\right)\)
\(\Rightarrow BE\perp AH\Rightarrow AH\perp\left(SBE\right)\)
\(\Rightarrow AH=d\left(A;\left(SBE\right)\right)\)
ACBE là hình bình hành (2 cặp cạnh đối song song) \(\Rightarrow AE=BC=AB=a\)
\(\Rightarrow\Delta ABE\) vuông cân tại A \(\Rightarrow AF=\dfrac{AB}{\sqrt{2}}=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng tam giác vuông SAF:
\(AH=\dfrac{AF.SA}{\sqrt{AF^2+SA^2}}=\dfrac{3a\sqrt{19}}{19}\)